
1.补写出下列名句名篇中的空缺部分。
(1)画图省识春风面,________________。(杜甫《咏怀古迹》)
(2)黄鹤之飞尚不得过,________________。青泥何盘盘,________________。(李白《蜀道难》)
(3)积善成德,________________,________________。(《荀子·劝学》)
(4)五亩之宅,________________,________________。(孟子《寡人之于国也》)
(5)然秦以区区之地,________________,________________,百有余年矣。(贾谊《过秦论》)
5.(2007年广东理12)如果一个凸多面体是n棱锥,那么这个凸多面体的所有顶点所确定的直线共有_____条,这些直线中共有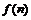 对异面直线,则
对异面直线,则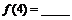 ;f(n)=______(答案用数字或n的解析式表示)
;f(n)=______(答案用数字或n的解析式表示)
答案: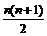 ;8;n(n-2)。解析:
;8;n(n-2)。解析: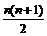 ;
;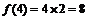 ;
;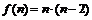
4.(2007年海南理16)某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种.(用数字作答)
[答案]:240[分析]:由题意可知有一个工厂安排2个班,另外三个工厂每厂一个班,
共有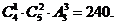 种安排方法。
种安排方法。
3.(2009年浙江理16)甲、乙、丙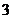 人站到共有
人站到共有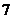 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站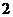 人,同一级台阶上的人不区分站的位置,则不同的站法种数是
(用数字作答).
人,同一级台阶上的人不区分站的位置,则不同的站法种数是
(用数字作答).
336 [解析]对于7个台阶上每一个只站一人,则有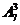 种;若有一个台阶有2人,另一个是1人,则共有
种;若有一个台阶有2人,另一个是1人,则共有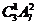 种,因此共有不同的站法种数是336种.
种,因此共有不同的站法种数是336种.
2.(2009年海南理15)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
解析: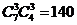 ,答案:140
,答案:140
1.(2010年浙江理17)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、 “台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共有______________种(用数字作答).
解析:本题主要考察了排列与组合的相关知识点,突出对分类讨论思想和数学思维能力的考察,属较难题
11.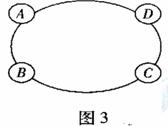 (2007年广东理7)图3是某汽车维修公司的维修点分布图,公司在年初分配给A、B、C、D四个维修点的某种配件各50件,在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行,那么完成上述调整,最少的调动件次(n个配件从一个维修点调整到相邻维修点的调动件次为n)为
(2007年广东理7)图3是某汽车维修公司的维修点分布图,公司在年初分配给A、B、C、D四个维修点的某种配件各50件,在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行,那么完成上述调整,最少的调动件次(n个配件从一个维修点调整到相邻维修点的调动件次为n)为
(A)15 (B)16 (C)17 (D)18
答案:B;
10.(2008年上海理12)组合数C(n>r≥1,n、r∈Z)恒等于( )
A.C B.(n+1)(r+1)C C.nr C D.C
[答案]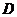 [解析]由
[解析]由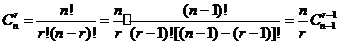 .
.
9.(2008年海南理9)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有( )
A.20种 B.30种 C.40种 D.60种
A解:分类计数:甲在星期一有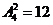 种安排方法,甲在星期二有
种安排方法,甲在星期二有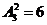 种安排方法,
种安排方法,
甲在星期三有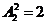 种安排方法,总共有
种安排方法,总共有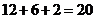 种,
种,
8.(2009年辽宁理5) 从5名男医生、4名女医生中选3名医生组成一个医疗小分队,要求男、女医生都有,则不同的组队方案共有
(A)70种 (B)80种 (C)100种 (D)140种
A 解析: 分2男1女、 1男2女两种情况,共有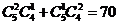 种不同的组队方案。
种不同的组队方案。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com