
5.按C、N、O、F顺序下列性质递增的是
A.最高化合价 B.非金属性
C.电子层数 D.原子半径
4.在元素周期表中,金属元素与非金属元素分界线附近,能找到
A.制农药的元素 B.制半导体材料的元素
C.制催化剂的元素 D.制耐高温合金的元素
3.下列产品的使用不会对环境造成污染的是
A.酒精 B.含磷洗衣粉
C.氟利昂 D.含汞电池
2.下列变化中,属于物理变化的是
A.煤的干馏 B.石油的裂化
C.石油的分馏 D.铝热反应
1.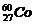 是γ放射源,可用于农作物诱变育种,我国用该方法培育出了许多农作物新品种,对
是γ放射源,可用于农作物诱变育种,我国用该方法培育出了许多农作物新品种,对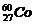 原子的叙述不正确的是
原子的叙述不正确的是
A.质量数是60 B.质子数是60
C.中子数是33 D.电子数是27
1.(2006重庆)已知定义域为R的函数f(x)满足f(f(x)-x2+x)=f(x)-x2+x.
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)=x0,求函数f(x)的解析表达式。
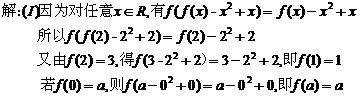
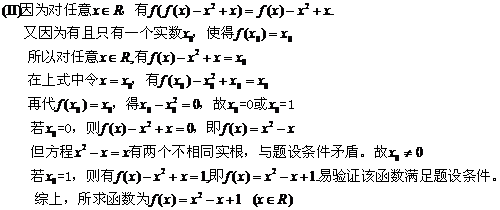 2.函数
2.函数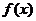 的定义域是
的定义域是 满足
满足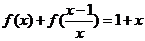 ,求
,求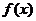 。
。
解:把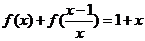 ①中的x换成
①中的x换成 得
得
 ②再把
②再把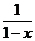 换得
换得
 ③
③
由①-②+③得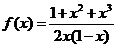
10.定义在R上的单调函数f(x)满足f(3)=log 3且对任意x,y∈R都有f(x+y)=f(x)+f(y). (1)求证f(x)为奇函数;
3且对任意x,y∈R都有f(x+y)=f(x)+f(y). (1)求证f(x)为奇函数;
(2)若f(k·3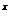 )+f(3
)+f(3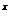 -9
-9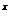 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
分析:欲证f(x)为奇函数即要证对任意x都有f(-x)=-f(x)成立.在式子f(x+y)=f(x)+f(y)中,令y=-x可得f(0)=f(x)+f(-x)于是又提出新的问题,求f(0)的值.令x=y=0可得f(0)=f(0)+f(0)即f(0)=0,f(x)是奇函数得到证明.
(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3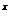 )<-f(3
)<-f(3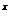 -9
-9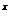 -2)=f(-3
-2)=f(-3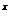 +9
+9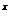 +2), k·3
+2), k·3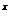 <-3
<-3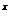 +9
+9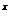 +2,
+2,
3 -(1+k)·3
-(1+k)·3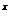 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3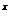 >0,问题等价于t
>0,问题等价于t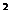 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
 综上所述:
综上所述:
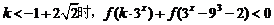 对任意x∈R恒成立。
对任意x∈R恒成立。
说明:问题(2)的上述解法是根据函数的性质.f(x)是奇函数且在x∈R上是增函数,把问题转化成二次函数f(t)=t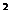 -(1+k)t+2对于任意t>0恒成立.对二次函数f(t)进行研究求解.本题还有更简捷的解法:
-(1+k)t+2对于任意t>0恒成立.对二次函数f(t)进行研究求解.本题还有更简捷的解法:
分离系数由k·3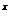 <-3
<-3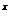 +9
+9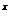 +2得
+2得

要使对 不等式
不等式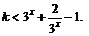 恒成立,
恒成立,
只需k<
上述解法是将k分离出来,然后用平均值定理求解,简捷、新颖.
[探索题]
9.设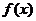 是定义在
是定义在 上的增函数,且对任意的
上的增函数,且对任意的 ,f(xy)=f(x)+f(y)总成立。 (1)求证:
,f(xy)=f(x)+f(y)总成立。 (1)求证: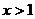 时,
时, ; (2)如果
; (2)如果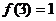 ,解不等式
,解不等式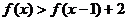
证明(1): 由f(xy)=f(x)+f(y),取x=y=1,f(1)=0,又f(x)递增,故x>1时,f(x)>0;
解(2):f(3)=1则2=f(3)+f(3)=f(9),从而f(x)>f(x-1)+2等价于F(x)>f(x-1)+f(9)=f(9x-9),
∵是增函数, ∴x>9x-9, ∴
8.已知函数 上有定义,对任意实数
上有定义,对任意实数 和任
和任
意实数 ,证明:(Ⅰ)
,证明:(Ⅰ)
(Ⅱ)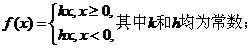
证明:(I)对于任意的 均有:
均有: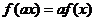 ①
①
在①中取
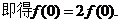

(II)证明:当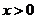 时,由①得:
时,由①得: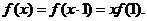
取 则有:
则有: ②
②
当x < 0时,由①得: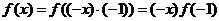
取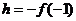 ,则有
,则有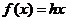 ③
③
综合②、③、得f(x)=
7.设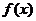 是定义在
是定义在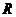 上的偶函数,其图象关于直线
上的偶函数,其图象关于直线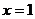 对称,对任意
对称,对任意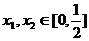 ,都有
,都有 . (I)设
. (I)设 ,求
,求 ; (II)证明
; (II)证明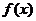 是周期函数.
是周期函数.
解(1):当x∈[0,1/2]时,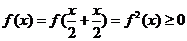 ,
,
 ; 同理
; 同理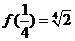
(2)是偶函数则(-x)=f(x),关于x=1对称则有f(x)=f(2-x)
∴f(x)=f(2-x)=f(x-2), ∴f(x)周期为2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com