
9.已知函数x,y满足x≥1,y≥1 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围
9 解: 由已知等式得loga2x+loga2y=(1+2logax)+(1+2logay),
即(logax-1)2+(logay-1)2=4,
令u=logax,v=logay,k=logaxy,则(u-1)2+(v-1)2=4(uv≥0),k=u+v
在直角坐标系uOv内,
圆弧(u-1)2+(v-1)2=4(uv≥0)与平行直线系v=-u+k有公共点,
分两类讨论
(1)当u≥0,v≥0时,即a>1时,结合判别式法与代点法得
1+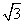 ≤k≤2(1+
≤k≤2(1+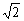 );
);
(2)当u≤0,v≤0,即0<a<1时,同理得到2(1-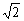 )≤k≤1-
)≤k≤1-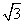

综上,当a>1时,logaxy的最大值为2+2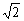 ,最小值为1+
,最小值为1+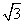 ;
;
当0<a<1时,logaxy的最大值为1-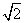 ,最小值为2-2
,最小值为2-2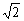
8. 已知函数f(x)=logax(a>0且a≠1),(x∈(0,+∞)),若x1,x2∈(0,+∞),判断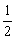 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(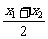 )的大小,并加以证明
)的大小,并加以证明
解 f(x1)+f(x2)=logax1+logax2=logax1x2,
f(x1)+f(x2)=logax1+logax2=logax1x2,
∵x1,x2∈(0,+∞),x1x2≤(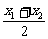 )2(当且仅当x1=x2时取“=”号),
)2(当且仅当x1=x2时取“=”号),
当a>1时,有logax1x2≤loga(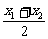 )2,
)2,
∴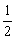 logax1x2≤loga(
logax1x2≤loga(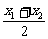 ),
),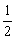 (logax1+logax2)≤loga
(logax1+logax2)≤loga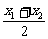 ,
,
即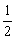
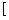 f(x1)+f(x2)]≤f(
f(x1)+f(x2)]≤f(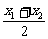 )(当且仅当x1=x2时取“=”号)
)(当且仅当x1=x2时取“=”号)
当0<a<1时,有logax1x2≥loga(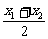 )2,
)2,
∴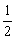 (logax1+logax2)≥loga
(logax1+logax2)≥loga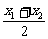 ,即
,即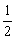 [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f(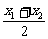 )(当且仅当x1=x2时取“=”号)
)(当且仅当x1=x2时取“=”号)
7. 设不等式2(log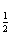 x)2+9(log
x)2+9(log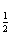 x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2 )(log2
)(log2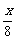 )的最大、最小值
)的最大、最小值
解 ∵2(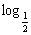 x)2+9(
x)2+9(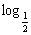 x)+9≤0
x)+9≤0
∴(2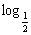 x+3)(
x+3)( 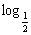 x+3)≤0 ∴-3≤
x+3)≤0 ∴-3≤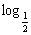 x≤-
x≤-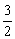
即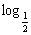 (
(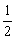 )-3≤
)-3≤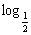 x≤
x≤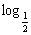 (
(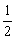 )
)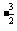 ?
?
∴(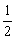 )
)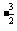 ≤x≤(
≤x≤(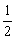 )-3,∴2
)-3,∴2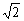 ≤x≤8
≤x≤8
即M={x|x∈[2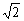 ,8]}
,8]}
又f(x)=(log2x-1)(log2x-3)=log22x-4log2x+3=(log2x-2)2-1
∵2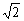 ≤x≤8,∴
≤x≤8,∴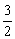 ≤log2x≤3
≤log2x≤3
∴当log2x=2,即x=4时ymin=-1;当log2x=3,即x=8时,ymax=0
6. 由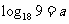 得
得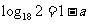 ,又
,又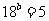 ,
,
∴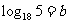 ,∴
,∴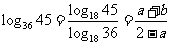
[解答题]
4.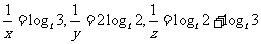 ,选B; 5.2;
,选B; 5.2;
6.已知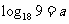 ,
,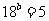 ,则
,则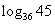 用 a, b
表示为
用 a, b
表示为
答案提示:
1-4.ACBB; 3.易得f(x)是偶函数,又在(-∞,0)上递增,∴f(x)在(0,+∞)上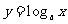 单调递减,0<a<1.
1<a+1<2.∴f(a+1)>f(2).
单调递减,0<a<1.
1<a+1<2.∴f(a+1)>f(2).
5.(2006江西)设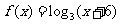 的反函数为
的反函数为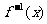 ,若
,若
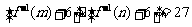 ,则
,则 ________.
________.
4.设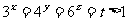 ,则
,则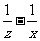 与
与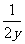 的大小关系为( )
的大小关系为( )
A.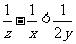 B.
B.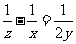
C.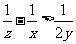 D.
D.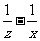 与
与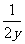 的大小关系不确定
的大小关系不确定
[填空题]
3.设函数f(x)=loga|x|在(-∞,0)上单调递增,则f(a+1)与f(2)的大小关系是 ( )
A.f(a+1)=f(2) B.f(a+1)>f(2)
C.f(a+1)<f(2) D.不能确定
2.若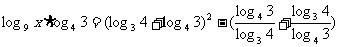 ,则
,则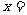 ( )
( )
A.4 B.16 C.256 D.81
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com