
1. (2006浙江)已知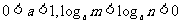 ,则 ( )
,则 ( )
A.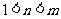 B.
B.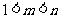 C.
C.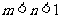 D.
D.
3.感悟知识、思想方法在解题 中的运用;
同步练习 2.10对数与对数函数
[选择题]
2.对数函数的定义、图象和性质:
1.对数的概念、运算性质:
3.解对数方程的方法--去对数符号。
[研讨.欣赏]设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,点Q(x-2a,-y)是函数y=g(x)图象上的点 (1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围
解: (1)设点Q的坐标为(x′,y′),
则x′=x-2a,y′=-y 即x=x′+2a,y=-y′
∵点P(x,y)在函数y=loga(x-3a)的图象上,
∴-y′=loga(x′+2a-3a),即y′=loga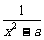 ,
,
∴g(x)=loga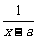
(2)由题意在[a+2,a+3]上x-3a≥(a+2)-3a=-2a+2>0;
又a>0且a≠1,∴0<a<1,
∵|f(x)-g(x)|=|loga(x-3a)-loga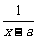 |=|loga(x2-4ax+3a2)|
|=|loga(x2-4ax+3a2)|
而|f(x)-g(x)|≤1, ∴-1≤loga(x2-4ax+3a2)≤1,
∵0<a<1, ∴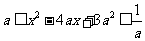
又 a+2>2a.知u(x)=x2-4ax+3a2在[a+2,a+3]上为增函数,
∴只需
解得0<a≤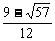 ,
,
∴所求a的取值范围是0<a≤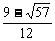
方法提炼 (1).求对称图象的函数解析式的方法;
(2).先去绝对值,再利用单调性列不等式组求a的取值范围.
[例1](1)若60a=3,60b=5.求12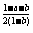 的值.
的值.
(2)已知315a=55b=153c,求证:5ab-bc-3ac=0
解(1) a=log603,b=log605,
1-b=1-log605=log6012,
1-a-b=1-log603-log605=log604,
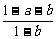 =
=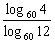 =log124,
=log124,
12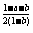 =12
=12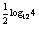 =12
=12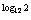 =2.
=2.
证(2) 设315a=55b=153c=k>0,则lg315a=lgk,
∴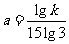 同理
同理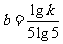 ,
,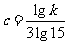
把上述三式代入得
5ab-bc-3ac=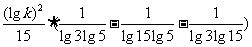
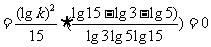
点评:注意指数式和对数式的灵活转化;注意对数运算性质的正确运用.
[例2](1)求函数
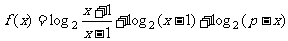 的值域.
的值域.
(2)设m=(log2x)2+(t-2)log2x+1-t,若t在区间[-2,2]上变化时,m值恒正,求x的取值范围.
解: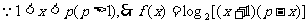
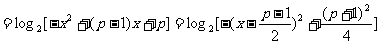 ①当
①当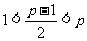 ,即
,即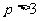 时,
时,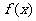 值域为
值域为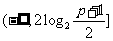 ;
;
②当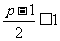 ,即
,即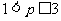 时,
时,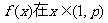 上单调递减,
上单调递减,
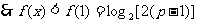 ,
,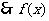 值域为
值域为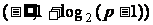
(2) m=(log2x-1)t+[(log2x)2-2log2x+1]关于变量t的图象是直线,要t∈[-2,2]时m值恒正,只要t=-2和2时m的值恒正,即有
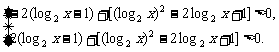
∴log2x>3或log2x<-1.
∴x>8或0<x<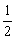 .
.
步骤归纳: (1)正确确定定义域; 转化为二次函数值域; 再分类讨论;
(2)转化为一次函数在[-2,2]上恒正问题; 再数形结合列出不等式组求m的范围.
[例3]已知函数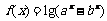
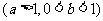 ,
,
(1)求f(x)的定义域;
(2)此函数的图象上是否存在两点,过这两点的直线平行于x轴?
(3)当a、b满足什么条件时f(x)恰在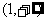 取正值.
取正值.
解:(1)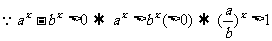 ,
,
又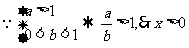 ,故函数的定义域是
,故函数的定义域是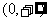 .
.
(2)问题的结论取决于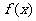 是否单调,考察单调性有三种方法:①求导,②运用单调性定义,③复合分析,但以方法①最好.
是否单调,考察单调性有三种方法:①求导,②运用单调性定义,③复合分析,但以方法①最好.
(解一)任取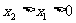 ,则
,则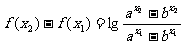 ,
,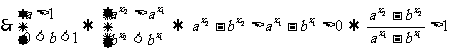
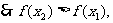 即
即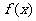 在定义域内单调递增,故不存在所述两点;
在定义域内单调递增,故不存在所述两点;
(解二)求导: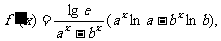
 ,
,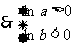 ,
,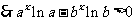 ,
,
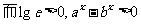
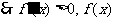 在定义域内单调递增,故不存在所述两点;
在定义域内单调递增,故不存在所述两点;
(3)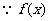 在
在 单调递增,∴命题等价于:
单调递增,∴命题等价于: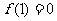 ,
,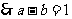
思维拓展 题(2)中证单调性的方法有--
[例4] 设a>0,a≠1,f(x)=loga(x+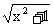 )
)
(1)判断函数f(x)的奇偶性;
(2)求函数的反函数f -1(x);
(3)若方程f(x)=loga(2x+ak)有实数解,求k的取值范围。
解 ∵x+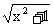 >x+|x|≥0 ∴f(x)定义域为R。
>x+|x|≥0 ∴f(x)定义域为R。
设u=x +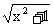 ,则u∈(0,+∞),f(x)值域为R。
,则u∈(0,+∞),f(x)值域为R。
(1)f(-x)=loga(-x+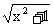 )
)
=loga(x+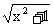 )-1=-f(x)
)-1=-f(x)
∴f(x)是奇函数。
(2)设y=loga(x+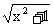 ),则
),则
ay=x+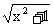 ,a-y=
,a-y=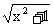 -x
-x
∴ay-a-y=2x x=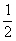 (ay-a-y)
(ay-a-y)
∴反函数f-1(x)=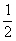 (ax-a-x) (x∈R)
(ax-a-x) (x∈R)
(3)由对数性质知loga(x+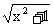 )=loga(2x+ak)
)=loga(2x+ak)
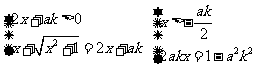
∴ 当k=0时,②无解,从而原方程无解。
当k≠0时,又a>0,由②得x=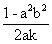 代入①得,
代入①得,
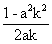 >-
>-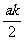 ∴
∴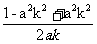 >0
>0
∴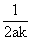 >0 ∴k>0
>0 ∴k>0
∴当k>0时,原方程有实数解。
解题札记:1.定义域优先;求出值域作反函数的定义域;
2.变形f(-x)=f(x)的方法--分子有理化;
4.当0<x<1时,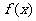 递减,
递减,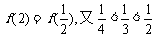 ,∴选C; 5.都换成2为底的对数,答案
,∴选C; 5.都换成2为底的对数,答案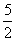 ;6.只须
;6.只须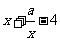 能取大于0的所有值,由
能取大于0的所有值,由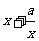 图象知
图象知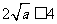 ,答案
,答案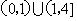 ; 7. 记u=logax,g(x)=u(u-
; 7. 记u=logax,g(x)=u(u-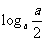 ),在
),在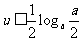 时递减,
时递减, 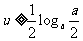 时递增.若0<a<1,则
时递增.若0<a<1,则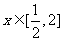 时,
时,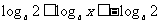 ,要使 g(x)递增必
,要使 g(x)递增必
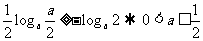 ,若a>1,同理可知无解.
,若a>1,同理可知无解.
所以,a的取值范围是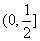
7.已知函数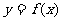 的图象与函数
的图象与函数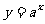 (
( 且
且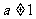 )的图象关于直线
)的图象关于直线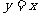 对称,记
对称,记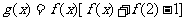 .若
.若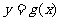 在区间
在区间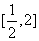 上是增函数,则实数
上是增函数,则实数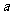 的取值范围是
的取值范围是
简答.精讲: 1-4.ABBC; 2.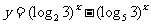 是增函数,x≥-y; 3.f(x)是奇函数, f(-a)=-f(a)=-b;
是增函数,x≥-y; 3.f(x)是奇函数, f(-a)=-f(a)=-b;
6.已知函数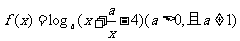 的值域为R,则实数a的取值范围是
.
的值域为R,则实数a的取值范围是
.
5.计算: = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com