
3. 已知函数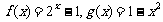 构造函数F(x),定义F如下:当
构造函数F(x),定义F如下:当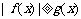 时,
时,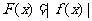 ,当
,当 时,
时,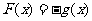 ,那么
,那么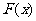 ( )
( )
A.有最小值-1,无最大值 B.有最小值0,无最大值
C.有最大值1,无最小值 D.无最小值,也无最大值
[填空题]
2.已知函数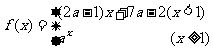 在(-∞,+∞)上单调递减,则实数a的取值范围是
( )
在(-∞,+∞)上单调递减,则实数a的取值范围是
( )
A.(0,1) B.(0,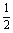 ) C.
) C. D.
D.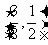
1.(2006山东)设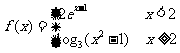 ,则不等式
,则不等式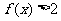 的解集为 ( )
的解集为 ( )
A.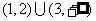 B.
B.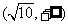 C.
C.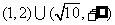 D.
D.
2.分段函数的处理方法:分段函数分段研究;解题中务必看清自变量在哪一段,该代哪个解析式。
同步练习 2.11分段函数与绝对值函数
[选择题]
1.分段函数、绝对值函数问题类型--
[例1]设定义在N上的函数f(x)满足f(n)=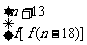
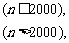 求f(2002).
求f(2002).
解:∵2002>2000,
∴f(2002)=f[f(2002-18)]=f[f(1984)]=f[1984+13]=f(1997)=1997+13=2010.
感悟方法 求值时代入哪个解析式,一定要看清自变量的取值在哪一段上.
[例2]判断函数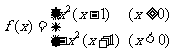 的奇偶性。
解:当x>0时,-x<0,
f(-x)=
-(-x)2(-x+1)=x2(x-1)=f(x);
当x=0时,f(-0)=f(0)=0;当x<0时,f(-x)=( -x)2(-x-1)= -x2(x+1)=f(x)。因此,对任意x∈R都有f(-x)=f(x),所以函数f(x)为偶函数。
提炼方法::分段函数的奇偶性必须对x的值分类比较f(-x)与f(x)的关系,得出f(x)是否是奇偶函数的结论。
的奇偶性。
解:当x>0时,-x<0,
f(-x)=
-(-x)2(-x+1)=x2(x-1)=f(x);
当x=0时,f(-0)=f(0)=0;当x<0时,f(-x)=( -x)2(-x-1)= -x2(x+1)=f(x)。因此,对任意x∈R都有f(-x)=f(x),所以函数f(x)为偶函数。
提炼方法::分段函数的奇偶性必须对x的值分类比较f(-x)与f(x)的关系,得出f(x)是否是奇偶函数的结论。
[例3](2007启东质检)已知函数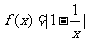 ,
,
(1)当 时,求证:
时,求证: ;
;
(2)是否存在实数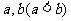 ,使得函数
,使得函数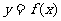 的定义域、值域都是
的定义域、值域都是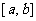 ,若存在,则求出
,若存在,则求出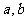 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若存在实数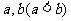 ,使得函数
,使得函数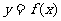 的定义域为
的定义域为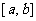 时,值域为
时,值域为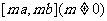 ,求m的取值范围.
,求m的取值范围.
解:(1)∵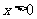 ,∴
,∴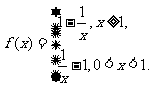
∴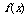 在(0,1)上为减函数,在(1,+∞)上是增函数.
在(0,1)上为减函数,在(1,+∞)上是增函数.
由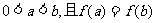 ,可得
,可得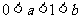 ,
,
所以有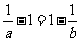 ,即
,即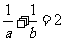 .∴
.∴
故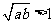 ,即
,即
(2)不存在满足条件的实数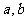 .
.
若存在满足条件的实数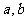 ,使得函数
,使得函数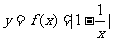 的定义域、值域都是[
的定义域、值域都是[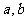 ],则
],则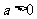 .由
.由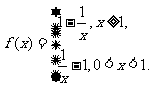
①当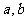 ∈(0,1)时,
∈(0,1)时,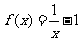 在(0,1)上为减函数.
在(0,1)上为减函数.
故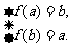 ,即
,即 ,解得
,解得 .
.
故此时不存在适合条件的实数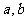 .
.
②当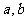 ∈
∈ 时,
时,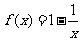 在(1,+∞)上为增函数.故
在(1,+∞)上为增函数.故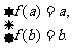 ,即
,即
此时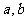 是方程
是方程 的根,由于此方程无实根.
的根,由于此方程无实根.
故此时不存在适合条件的实数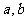 .
.
③当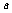 ∈(0,1),
∈(0,1),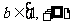 时,由于1∈[
时,由于1∈[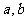 ],而
],而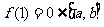 ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数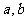 .
.
综上可知,不存在适合条件的实数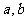 .
.
(3)若存在实数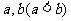 ,使得函数
,使得函数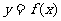 的定义域为[
的定义域为[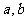 ]时,值域为
]时,值域为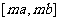 ,则
,则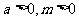 .
.
①当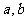 ∈(0,1)时,由于
∈(0,1)时,由于 在(0,1)上是减函数,值域为
在(0,1)上是减函数,值域为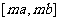 ,
,
即 解得a=b>0,不合题意,所以
解得a=b>0,不合题意,所以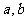 不存在.
不存在.
②当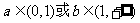 时,由(2)知0在值域内,值域不可能是
时,由(2)知0在值域内,值域不可能是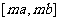 ,所以
,所以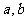 不存在.故只有
不存在.故只有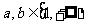 .
.
∵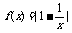 在(1,+∞)上是增函数,∴
在(1,+∞)上是增函数,∴ ,即
,即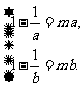
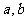 是方程
是方程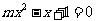 有两个根.
有两个根.
即关于x的方程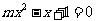 有两个大于1的实根.
有两个大于1的实根.
设这两个根为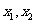 .则
.则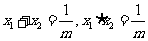
∴ 即
即
解得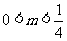 .
.
综上m的取值范围是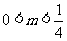 .
.
[例4]设a为实数,设函数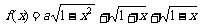 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=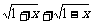 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(Ⅱ)求g(a);
解:(I)∵t=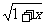 +
+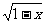 ,
,
∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
∵t2=2+2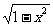 ∈[2,4],t≥0,
①
∈[2,4],t≥0,
①
∴t的取值范围是[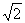 ,2].
,2].
由①得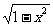 =
=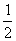 t2-1,
t2-1,
∴m(t)=a(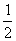 t2-1)+t=
t2-1)+t=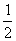 at2+t-a,t∈[
at2+t-a,t∈[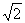 ,2].
,2].
(Ⅱ)由题意知g(a)即为函数m(t)=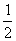 at2+t-a, t∈[
at2+t-a, t∈[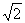 ,2]的最大值.
,2]的最大值.
注意到直线t=-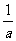 是抛物线m(t)=
是抛物线m(t)= 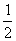 at2+t-a的对称轴,分以下几种情况讨论.
at2+t-a的对称轴,分以下几种情况讨论.
(1)当a>0时,函数y=m(t), t∈[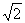 ,2]的图像是开口向上的抛物线的一段,由
,2]的图像是开口向上的抛物线的一段,由
t=-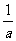 <0知m(t)在[
<0知m(t)在[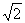 ,2]上单调递增,
,2]上单调递增,
∴g(a)=m(2)=a+2.
(2)当a=0时,m(t)=t,t∈[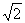 ,2], ∴g(a)=2.
,2], ∴g(a)=2.
(3)当a<0时,函数y=m(t), t∈[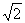 ,2]的图像是开口向下的抛物线的一段.
,2]的图像是开口向下的抛物线的一段.
若t=-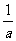 ∈(0,
∈(0,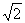 ],即a≤-
],即a≤-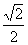 ,则g(a)=m(
,则g(a)=m(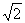 )=
)=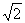 .
.
若t=-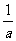 ∈(
∈(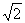 ,2],即a∈(-
,2],即a∈(-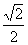 ,-
,-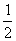
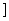 则g(a)=m(-
则g(a)=m(-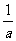 )=-a-
)=-a-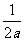 .
.
若t=-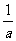 ∈(2,+ ∞),即a∈(-
∈(2,+ ∞),即a∈(-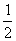 ,0),则g(a)=m(2)=a+2.
,0),则g(a)=m(2)=a+2.
综上有g(a)=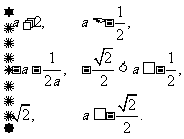
核心步骤:(1) m(t)=a(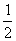 t2-1)+t=
t2-1)+t=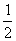 at2+t-a,t∈[
at2+t-a,t∈[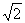 ,2].
,2].
(2)求g(a)=[m(t)]max,按对称轴相对于区间[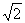 ,2]的位置,对a分类分类讨论.
,2]的位置,对a分类分类讨论.
 [研讨.欣赏](2000全国)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
[研讨.欣赏](2000全国)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P=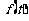 ;
;
写出图二表示的种植成本与时间的函数关系式Q=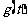 ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/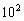 kg,时间单位:天)
kg,时间单位:天)
解:(Ⅰ)由图一可得市场售价与时间的函数关系为
f(t)=
由图二可得种植成本与时间的函数关系为
g(t)=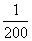 (t-150)2+100,0≤t≤300.
(t-150)2+100,0≤t≤300.
(Ⅱ)设t时刻的纯收益为h(t),则由题意得
h(t)=f(t)-g(t)
即h(t)=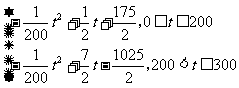
当0≤t≤200时,配方整理得
h(t)=-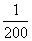 (t-50)2+100,
(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得
h(t)=-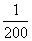 (t-350)2+100
(t-350)2+100
所以,当t=300时,h(t)取得区间[200,300]上的最大值87.5.
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
思路点拨: 题(Ⅱ)分段写出收益与时间的函数关系h(t), 是分段函数,再分段求最值.
7.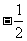 ;8. 当x≥0时,x2+1≥1;当x<0时,-x2<0原函数值域是[1,+∞]∪(-∞,0)。
;8. 当x≥0时,x2+1≥1;当x<0时,-x2<0原函数值域是[1,+∞]∪(-∞,0)。
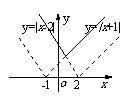
6. 由 ,
,
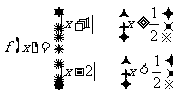 如右图
如右图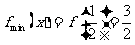
5. f(lg30-lg3)=f(lg10)=f(1)=-2,
f(x-1)=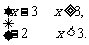
当x≥3时,x(x-3)<10 -2<x<5,故3≤x<5.
-2<x<5,故3≤x<5.
当x<3时,-2x<10 x>-5,故-5<x<3.解集
{x|-5<x<5}
x>-5,故-5<x<3.解集
{x|-5<x<5}
4.x=10时,取最小值90.f(x)=|x-1|+|x-2|+…+|x-19|
=|x-1|+…+|x-10|+|11-x|+…+|19-x|
≥|x-1+x-2+…x-9+11-x+…19-x|+|x-10|
 ≥|90|+0=90, 当x=10时取等号.一般地:…
≥|90|+0=90, 当x=10时取等号.一般地:…
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com