
若p q,q
q,q p;则
p;则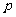 是
是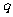 的充分非必要条件
的充分非必要条件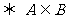 ;
;
若p q,q
q,q p;则
p;则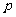 是
是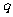 的必要非充分条件
的必要非充分条件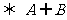 ;
;
若p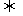 q;则
q;则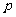 是
是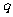 的充要条件
的充要条件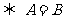 ;
;
若p q,q
q,q p;则
p;则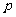 是
是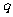 的既非充分又非必要条件
的既非充分又非必要条件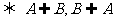 ;
;
(1)若集合 中有
中有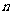 个元素,则集合
个元素,则集合 的所有不同的子集个数为2
的所有不同的子集个数为2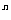 ,所有真子集的个数是2
,所有真子集的个数是2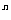 -1,所有非空真子集的个数是2
-1,所有非空真子集的个数是2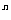 -2。
-2。
(2)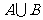 中元素的个数的计算公式为:
中元素的个数的计算公式为:
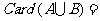

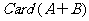 ;
;
(3)韦恩图的运用:
(1)符号“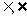 ”是表示元素与集合之间关系的,立体几何中的体现
点与直线(面)的关系
;
”是表示元素与集合之间关系的,立体几何中的体现
点与直线(面)的关系
;
符号“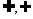 ”是表示集合与集合之间关系的,立体几何中的体现
面与直线(面)的关系
。
”是表示集合与集合之间关系的,立体几何中的体现
面与直线(面)的关系
。
(2)A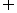 B={
x| x
B={
x| x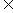 A且x
A且x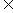 B} A
B} A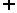 B={
x| x
B={
x| x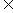 A或x
A或x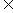 B};
B};
C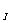 A={
x| x
A={
x| x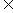 I且x
I且x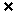 A}
A}
(3)对于任意集合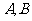 ,则:
,则:
①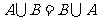 ;
;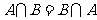 ;
;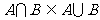 ;
;
②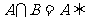 A
A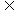 B;
B;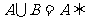 B
B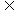 A
;
A
;
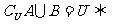 A
A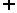 B=
B=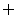 ;
;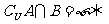 A
A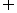 B=U;
B=U;
③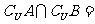
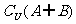 ;
; 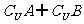
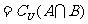 ;
;
(4)①若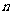 为偶数,则
为偶数,则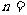 2K,(k
2K,(k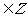 );若
);若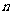 为奇数,则
为奇数,则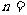 2k+1, (k
2k+1, (k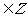 );
);
②若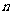 被3除余0,则
被3除余0,则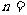 3k, (k
3k, (k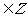 );若
);若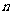 被3除余1,则
被3除余1,则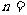 3k+1(k
3k+1(k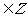 );若
);若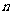 被3除余2,则
被3除余2,则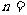 3k+2(k
3k+2(k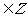 );
);
(1)集合中元素的特征:确定性,互异性,无序性 。
(2)集合与元素的关系用符号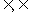 表示。
表示。
(3)常用数集的符号表示:自然数集
N ;正整数集 N 、
N
、
N ;整数集 Z ;有理数集 Q 、实数集 R 。
;整数集 Z ;有理数集 Q 、实数集 R 。
(4)集合的表示法:列举法,描述法,符号法(数轴法,韦恩图法)
注意:区分集合中元素的形式:如: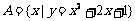 ;
;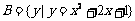 ;
;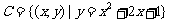
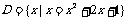 ;
;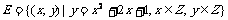 ;
;
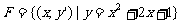 ;
;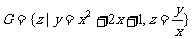
(5)空集是指不含任何元素的集合。(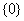 、
、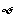 和
和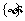 的区别;0与三者间的关系)
的区别;0与三者间的关系)
空集是任何集合的子集,是任何非空集合的真子集。
注意:条件为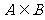 ,在讨论的时候不要遗忘了
,在讨论的时候不要遗忘了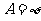 的情况。
的情况。
如: ,如果
,如果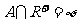 ,求
,求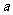 的取值。
的取值。
14.(重庆卷11)设集合U={1,2,3,4,5},A={2,4},B={3,4,5},C={3,4},则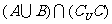 = .
= .
13.(江苏卷4)A=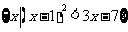 ,则A
,则A 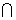 Z 的元素的个数 .
Z 的元素的个数 .
12.(辽宁卷1)已知集合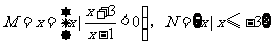 ,则集合
,则集合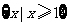 =( )
=( )
A.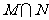 B.
B.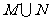 C.
C.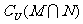 D.
D.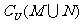
11.已知U=R,A=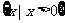 ,B=
,B=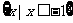 ,则
,则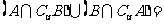
10.(福建卷2)设集合A={x|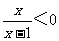 },B={x|0<x<3=,那么“m
},B={x|0<x<3=,那么“m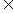 A”是“m
A”是“m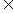 B”的
条件
B”的
条件
9.设m,n是整数,则“m,n均为偶数”是“m+n是偶数”的 条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com