
1.有限个函数的和(或积)的极限等于这些函数极限的和(或积),在求几个函数的和(或积)的极限时,一般要化简,再求极限;
[例1]求下列各极限:
(1)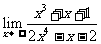
(2)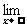 (
(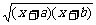 -x);
-x);
(3) 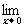
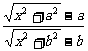 .(a>0)
.(a>0)
解:(1)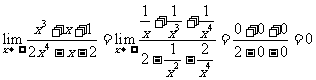
(2)原式=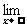
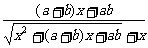 =a+b
=a+b
(3) 原式=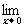

=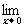
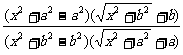
=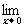
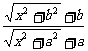 =
=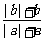
=
提炼方法:1.对于题(1)“ ”要先除以x的最高次方;题(2)“∞-∞”要先有理化,然后再求极限;
”要先除以x的最高次方;题(2)“∞-∞”要先有理化,然后再求极限;
2.在题(3)中,当b<0时,f(x)= 在x=0处连续,极限值就等于f(0).当b>0时, f (x)在x0处不连续,x→0时,分母为零,要先有理化,去掉掉分母为零的式子,再求极限.
在x=0处连续,极限值就等于f(0).当b>0时, f (x)在x0处不连续,x→0时,分母为零,要先有理化,去掉掉分母为零的式子,再求极限.
[例2](1)设f(x)=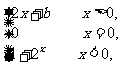 试确定b的值,使
试确定b的值,使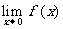 存在.
存在.
(2)f
(x)为多项式,且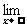
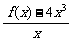 =1,
=1,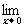
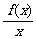 =5,求f(x)的表达式
=5,求f(x)的表达式
解:(1)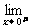 f (x)=
f (x)= 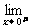 (2x+b)=b,
(2x+b)=b,
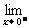 f(x)=
f(x)= 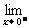 (1+2x)=2,
(1+2x)=2,
当且仅当b=2时,
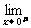 f (x)=
f (x)= 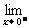 f (x),
f (x),
故b=2时,原极限存在
(2)由于f(x)是多项式,且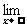
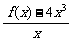 =1,
=1,
∴可设f (x)=4x3+x2+ax+b(a、b为待定系数)
又∵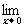
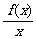 =5,
=5,
即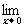 (4x2+x+a+
(4x2+x+a+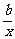 )=5,
)=5,
∴a=5,b=0, 即f (x)=4x3+x2+5x
点评:(1)理解极限的定义和极限存在的条件;
(2)初等函数在其定义域内每点的极限值就等于这一点的函数值.
[例3]已知函数f (x)=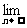
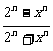 ,试求:
,试求:
(1)f (x)的定义域,并画出图象;
(2)求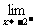 f (x)、
f (x)、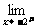 f (x),并指出
f (x),并指出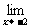 f (x)是否存在.
f (x)是否存在.
解:(1)当|x|>2时,
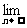
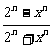 =
=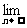
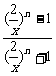 =-1;
=-1;
当|x|<2时,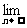
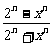 =
=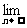
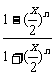 =1;
=1;
当x=2时,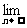
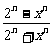 =0;
=0;
当x=-2时,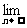
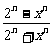 不存在.
不存在.
∴f (x)=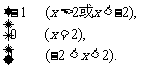
∴f (x)的定义域为{x|x<-2或x=2或x>2}.
如下图:
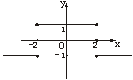
(2)∵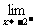 f (x)=-1,
f (x)=-1,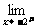 f (x)=1.∴
f (x)=1.∴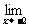 f (x)不存在.
f (x)不存在.
[例4]讨论函数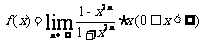 的连续性,并作出函数的图象.
的连续性,并作出函数的图象.
分析:应先求出f (x)的解析式,再判断连续性.
解:当0≤x<1时,f (x)= 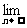
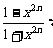 x=x;
x=x;
当x>1时,f (x)= 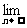
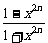 ·x=
·x=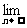
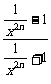 ·x=-x;
·x=-x;
当x=1时,f (x)=0.
∴f (x)=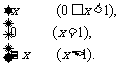
∵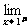 f(x)=
f(x)=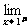 (-x)=-1,
(-x)=-1,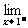 f(x)=
f(x)= 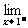 x=1,
x=1,
∴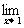 f(x)不存在.
f(x)不存在.
∴f (x)在x=1处不连续,f (x)在定义域内的其余点都连续.
图象如下图所示.
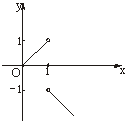
提炼方法: 分段函数讨论连续性,要讨论在“分界点”的左、右极限,进而判断连续性.
[研讨.欣赏]设f(x)在(a,b)内连续,如果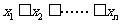 为(a,b)内的任意n个点.求证:在[x1,xn]上至少存在一点x0,使得
为(a,b)内的任意n个点.求证:在[x1,xn]上至少存在一点x0,使得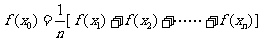
证明:由连续函数的性质,f(x)在闭区间[x1,xn]上必有最大值M,和最小值m,从而
m≤f(xi)≤M,(i=1,2,……n).
∴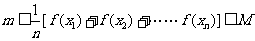 ,从而必有x0,使
,从而必有x0,使
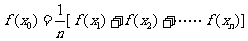 .
.
6.
f (0)=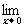 f (x)=
f (x)= 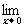
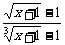 =
= 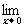
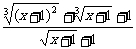 =
=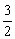
4. 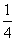 ; 5.
; 5. 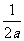 ;
;
3.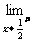 f(x)=
f(x)= 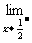 f(x)=f(
f(x)=f(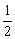 ).
).
6.要使f (x)=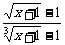 在点x=0处连续,则需补充定义f (0)=______
在点x=0处连续,则需补充定义f (0)=______
简答:1-3.DCD;
5.
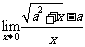 =______
=______
4.(2006广东) 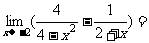
3.已知函数f(x)=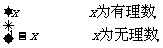 函数f(x)在哪点连续
函数f(x)在哪点连续
A.处处连续 B.x=1 C.x=0 D.x=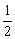
2.设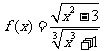 下列说法不正确的是 ( )
下列说法不正确的是 ( )
A.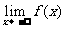 =1
B.
=1
B. 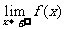 =1
=1
C. 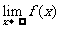 =1 D.
=1 D. 时f(x)极限不存在
时f(x)极限不存在
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com