
1、在直角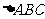 中,
中,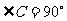 ,
,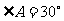 ,
,
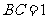 ,
,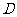 为斜边
为斜边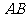 的中点,则
的中点,则 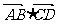 = 。
= 。
1 参数方程
参数方程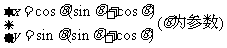 表示什么曲线?
表示什么曲线?
2 点
点 在椭圆
在椭圆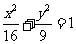 上,求点
上,求点 到直线
到直线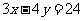 的最大距离和最小距离
的最大距离和最小距离
3 已知直线
已知直线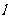 经过点
经过点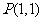 ,倾斜角
,倾斜角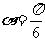 ,
,
(1)写出直线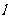 的参数方程
的参数方程
(2)设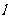 与圆
与圆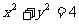 相交与两点
相交与两点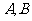 ,求点
,求点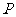 到
到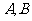 两点的距离之积
两点的距离之积
1 曲线的参数方程是
曲线的参数方程是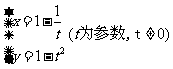 ,则它的普通方程为__________________
,则它的普通方程为__________________
2 直线
直线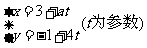 过定点_____________
过定点_____________
3 点
点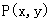 是椭圆
是椭圆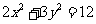 上的一个动点,则
上的一个动点,则 的最大值为___________
的最大值为___________
4 曲线的极坐标方程为
曲线的极坐标方程为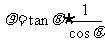 ,则曲线的直角坐标方程为________________
,则曲线的直角坐标方程为________________
5 设
设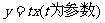 则圆
则圆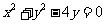 的参数方程为__________________________
的参数方程为__________________________
1 直线
直线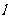 的参数方程为
的参数方程为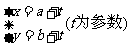 ,
,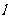 上的点
上的点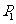 对应的参数是
对应的参数是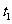 ,则点
,则点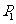 与
与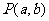 之间的距离是( )
之间的距离是( )
A
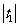 B
B
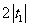 C
C
 D
D
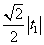
2 参数方程为
参数方程为 表示的曲线是( )
表示的曲线是( )
A 一条直线 B
一条直线 B 两条直线 C
两条直线 C 一条射线 D
一条射线 D 两条射线
两条射线
3 直线
直线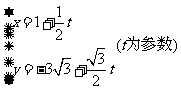 和圆
和圆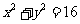 交于
交于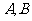 两点,
两点,
则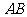 的中点坐标为( )
的中点坐标为( )
A
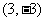 B
B
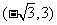 C
C
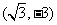 D
D
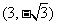
4 圆
圆 的圆心坐标是( )
的圆心坐标是( )
A
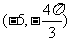 B
B
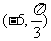 C
C
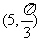 D
D
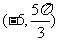
5 与参数方程为
与参数方程为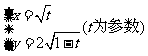 等价的普通方程为( )
等价的普通方程为( )
A
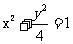 B
B
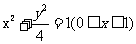
C
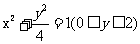 D
D
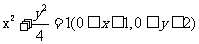
6 直线
直线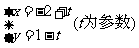 被圆
被圆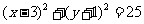 所截得的弦长为( )
所截得的弦长为( )
A
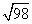 B
B
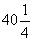 C
C
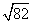 D
D
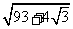
1.已知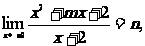 求
求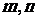
解法一: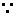
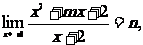
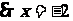 为方程
为方程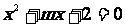 的一根,得
的一根,得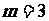 ,代人可得
,代人可得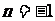
解法二:
 =
=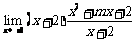
=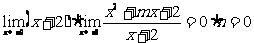
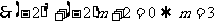 ,代人可得
,代人可得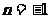
10. 设f(x)是x的三次函数,已知
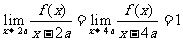 .试求
.试求 的值,(a为非零常数).
的值,(a为非零常数).
解:由已知可设f(x)=A(x-2a)(x-4a)(x-c),且有
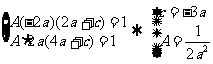

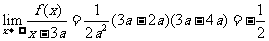
[探索题]在一个以AB为弦的弓形中,C为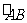 的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求
的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求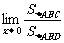 .
.
解:设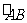 所在圆圆心为O,则C、D、O都在AB的中垂线上,
所在圆圆心为O,则C、D、O都在AB的中垂线上,
∴∠AOD=∠BOD=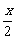 .设OA=r.
.设OA=r.
S△ABC=S四边形AOBC-S△AOB=r2sin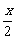 -
-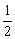 r2sinx=r2sin
r2sinx=r2sin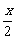 (1-cos
(1-cos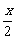 ),
),
S△ABD=S四边形AOBD-S△AOB=r2tan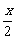 -
-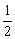 r2sinx=r2
r2sinx=r2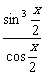 .
.
∴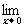
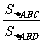 =
=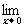
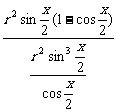 =
=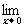
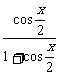 =
=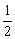 .
.
备题
9. 设f(x)=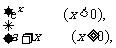 当a为何值时,函数f(x)是连续的
当a为何值时,函数f(x)是连续的
解: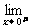 f(x)=
f(x)= 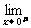 (a+x)=a,
(a+x)=a,
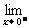 f(x)=
f(x)=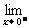 ex=1,而f(0)=a,故当a=1时,
ex=1,而f(0)=a,故当a=1时,
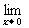 f(x)=f(0),
f(x)=f(0),
即说明函数f(x)在x=0处连续,而在x≠0时,f(x)显然连续,于是我们可判断当a=1时, f(x)在(-∞,+∞)内是连续的
8.
设函数f(x)=ax2+bx+c是一个偶函数,且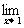 f(x)=0,
f(x)=0,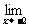 f(x)=-3,求出这一函数最大值
f(x)=-3,求出这一函数最大值
解:∵f (x)=ax2+bx+c是一偶函数, ∴f (-x)=f (x),
即ax2+bx+c=ax2-bx+c
∴b=0 ∴f (x)=ax2+c
又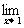 f (x)=
f (x)= 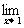 ax2+c=a+c=0,
ax2+c=a+c=0, 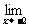 f(x)=
f(x)=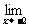 ax2+c=4a+c=-3,
ax2+c=4a+c=-3,
∴a=-1,c=1 ∴f (x)=-x2+1
∴f (x)max=f(0)=1 ∴f (x)的最大值为1
7.求下列函数的极限:
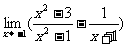
(1)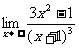 (2)
(2)
(3) 设f(x)=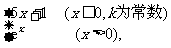 求
求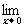 f(x)
f(x)
解:(1)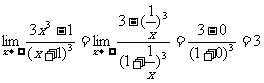
(2)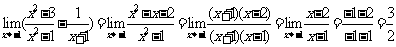
(3) 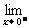 f(x)=1,
f(x)=1, 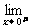 f(x)=1,
f(x)=1,
∴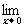 f(x)=1.
f(x)=1.
5.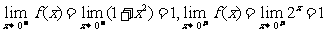
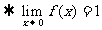 . 6.
. 6.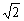
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com