
3.下列各句中标点符号使用正确的一句是
A.在当前的社会转型中,一方面生产力飞速发展、经济潜力被不断发掘,另一方面原有的制度每每缺乏活力、渐趋僵化。
B.有人把“民生”分为两类:一类是生存型,一类是发展型;由生存型到发展型就是由“填饱肚子”到“体面地生活”。
C.我厌倦了现在的生活;我开始醒悟,开始反思。我渴望回到我以前的生活状态--说自己想说的话,做自己想做的事。
D.郑板桥任潍县知县(今潍坊市区)有七年时间。当时潍县发生了百年不遇的大旱,他果断采取措施,开仓赈贷,救济灾民。
2.下列词语中没有错别字的一组是
A.观摩 闭门羹 首屈一指 真人不露像
B.屏障 拌脚石 作壁上观 朽木不可雕
C.遨翔 穷折腾 真知灼见 物以稀为贵
D.厮杀 杀风景 川流不息 高义薄云天
1.下列词语中加点的字,每对的读音都不相同的一组是
A.悭吝/缄默不语 粗犷/心旷神怡 挑剔/精挑细选
B.剽窃/彪炳千古 畸形/崎岖不平 提防/提纲挈领
C.赠送/锃光瓦亮 对峙/恃才傲物 积攒/攒三聚五
D.果脯/璞玉浑金 推诿/萎靡不振 伺候/伺机而动
1 分别在下列两种情况下,把参数方程
分别在下列两种情况下,把参数方程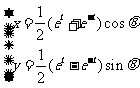 化为普通方程:
化为普通方程:
(1) 为参数,
为参数, 为常数;(2)
为常数;(2) 为参数,
为参数,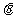 为常数;
为常数;
2 过点
过点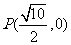 作倾斜角为
作倾斜角为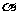 的直线与曲线
的直线与曲线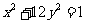 交于点
交于点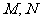 ,
,
求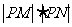 的值及相应的
的值及相应的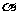 的值
的值
1 已知曲线
已知曲线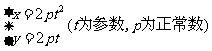 上的两点
上的两点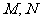 对应的参数分别为
对应的参数分别为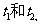 ,
, ,那么
,那么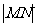 =_______________
=_______________
2 直线
直线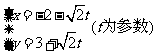 上与点
上与点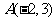 的距离等于
的距离等于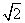 的点的坐标是_______
的点的坐标是_______
3 圆的参数方程为
圆的参数方程为 ,则此圆的半径为_______________
,则此圆的半径为_______________
4 极坐标方程分别为
极坐标方程分别为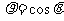 与
与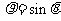 的两个圆的圆心距为_____________
的两个圆的圆心距为_____________
5 直线
直线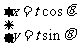 与圆
与圆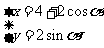 相切,则
相切,则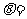 _______________
_______________
1 把方程
把方程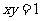 化为以
化为以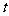 参数的参数方程是( )
参数的参数方程是( )
A
 B
B
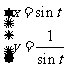 C
C
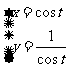 D
D
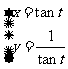
2 曲线
曲线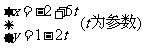 与坐标轴的交点是( )
与坐标轴的交点是( )
A
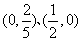 B
B
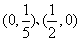 C
C
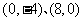 D
D
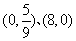
3 直线
直线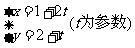 被圆
被圆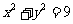 截得的弦长为( )
截得的弦长为( )
A
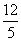 B
B
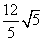 C
C
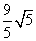 D
D
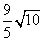
4 若点
若点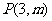 在以点
在以点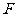 为焦点的抛物线
为焦点的抛物线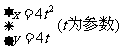 上,则
上,则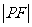 等于( )
等于( )
A
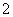 B
B
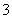 C
C
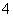 D
D
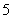
5 极坐标方程
极坐标方程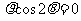 表示的曲线为( )
表示的曲线为( )
A 极点 B
极点 B 极轴 C
极轴 C 一条直线 D
一条直线 D 两条相交直线
两条相交直线
6 在极坐标系中与圆
在极坐标系中与圆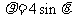 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A
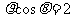 B
B
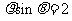 C
C
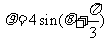 D
D
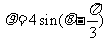
10、设函数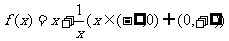 的图象为
的图象为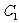 、
、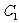 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为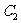 ,
,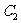 对应的函数为
对应的函数为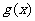 , (Ⅰ)求函数
, (Ⅰ)求函数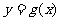 的解析式,并确定其定义域;
的解析式,并确定其定义域;
(Ⅱ)若直线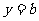 与
与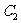 只有一个交点,求
只有一个交点,求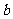 的值,并求出交点的坐标.
的值,并求出交点的坐标.
(Ⅰ)设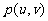 是
是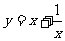 上任意一点,
上任意一点,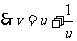 ① 设P关于A(2,1)对称的点为
① 设P关于A(2,1)对称的点为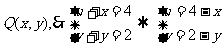 代入①得
代入①得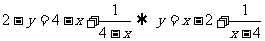
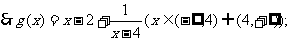
(Ⅱ)联立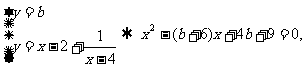
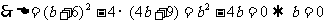 或
或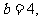
(1)当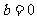 时得交点(3,0); (2)当
时得交点(3,0); (2)当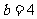 时得交点(5,4).
时得交点(5,4).
[探索题]设曲线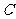 的方程是
的方程是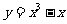 ,将
,将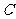 沿
沿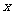 轴、
轴、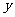 轴正方向分别平移
轴正方向分别平移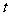 、
、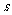
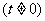 个单位长度后得到曲线
个单位长度后得到曲线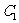 ,
,
(1)写出曲线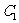 的方程;
的方程;
(2)证明曲线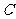 与
与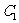 关于点
关于点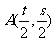 对称;
对称;
(3)如果曲线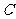 与
与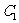 有且仅有一个公共点,证明:
有且仅有一个公共点,证明: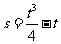 。
。
解:(1)曲线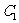 的方程为
的方程为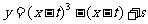 ;
;
(2)证明:在曲线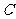 上任意取一点
上任意取一点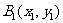 ,设
,设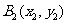 是
是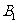 关于点
关于点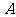 的对称点,则有
的对称点,则有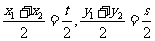 ,
,
∴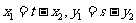 代入曲线
代入曲线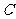 的方程,得
的方程,得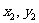 的方程:
的方程: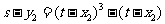
即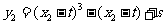 可知点
可知点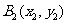 在曲线
在曲线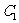 上。
上。
反过来,同样证明,在曲线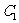 上的点
上的点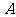 的对称点在曲线
的对称点在曲线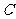 上。
上。
因此,曲线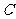 与
与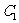 关于点
关于点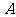 对称。
对称。
(3)证明:因为曲线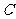 与
与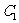 有且仅有一个公共点,
有且仅有一个公共点,
∴方程组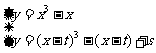 有且仅有一组解,
有且仅有一组解,
消去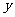 ,整理得
,整理得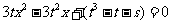 ,这个关于
,这个关于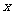 的一元二次方程有且仅有一个根,
的一元二次方程有且仅有一个根,
∴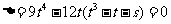 ,即得
,即得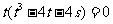 ,
,
因为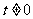 ,所以
,所以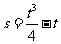 。
。
9、(2003重庆诊断题)已知函数f(x)=m(x+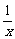 )的图象与函数h(x)=
)的图象与函数h(x)=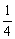 (x+
(x+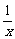 )+2的图象关于点A(0,1)对称.
)+2的图象关于点A(0,1)对称.
(1)求m的值;
(2)若g(x)=f(x)+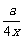 在区间(0,2]上为减函数,求实数a的取值范围.
在区间(0,2]上为减函数,求实数a的取值范围.
解:(1)设P(x,y)为函数h(x)图象上一点,点P关于A的对称点为Q(x′,y′),
则有x′=-x,且y′=2-y.
∵点Q(x′,y′)在f(x)=m(x+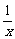 )上,
)上,
∴y′=m(x′+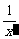 ).
).
将x、y代入,得2-y=m(-x-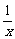 ).
).
整理,得y=m(x+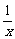 )+2.∴m=
)+2.∴m=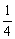 .
.
(2)∵g(x)=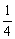 (x+
(x+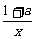 ),设x1、x2∈(0,2],且x1<x2,
),设x1、x2∈(0,2],且x1<x2,
则g(x1)-g(x2)=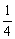 (x1-x2)·
(x1-x2)·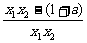 >0对一切x1、x2∈(0,2]恒成立.
>0对一切x1、x2∈(0,2]恒成立.
∴x1x2-(1+a)<0对一切x1、x2∈(0,2]恒成立.
∴由1+a>x1x2,而x1x2<4∴a≥3.
8、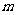 为何值时,直线
为何值时,直线 与曲线
与曲线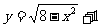 有两个公共点?有一个公共点?无公共点?
有两个公共点?有一个公共点?无公共点?
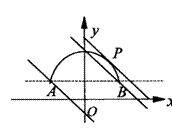 解:作出
解:作出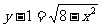 的图象(如图半圆)与
的图象(如图半圆)与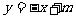 的图象(如图平行的直线,将
的图象(如图平行的直线,将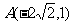 代入
代入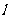 得
得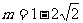 ,将
,将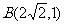 代入
代入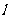 得
得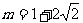 ,当
,当 与半圆相切于P时可求得
与半圆相切于P时可求得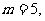
则①当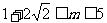 时,
时,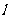 与曲线有两个公共点;
与曲线有两个公共点;
②当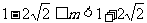 或
或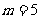 时,有一个公共点;
时,有一个公共点;
③当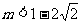 或
或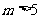 时,无公共点;
时,无公共点;
7.(1) (2) (3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com