
19、甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约;乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是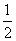 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率; 

(2)签约人数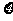 的分布列和数学期望.
的分布列和数学期望.
18、设函数 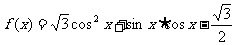
(1)求函数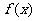 的最小正周期T,并求出函数
的最小正周期T,并求出函数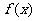 的单调递增区间。
的单调递增区间。
(2)求在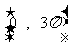 内使得
内使得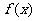 取到最大值的所有
取到最大值的所有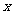 的和。
的和。
17、给出下列4个命题:
①函数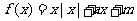 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数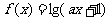 的定义域是
的定义域是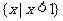 ,则
,则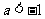 ;
;
③若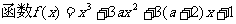 既有极大值又有极小值,则
既有极大值又有极小值,则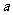 取值范围为
取值范围为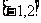 ;
;
④圆: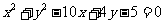 上任意点M关于直线
上任意点M关于直线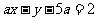 的对称点
的对称点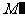 也在该圆上. 填上所有正确命题的序号是______.
也在该圆上. 填上所有正确命题的序号是______.
16、定义域为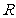 的函数
的函数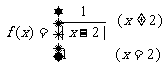 ,若关于
,若关于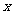 的方程
的方程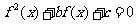 恰有5个不同的实数解
恰有5个不同的实数解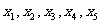 ,
,
则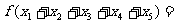 .
. 

15、已知直线y=x+1与椭圆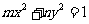 (m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于
(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于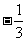 ,则双曲线
,则双曲线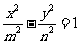 的两条渐近线的夹角的正切值等于__.
的两条渐近线的夹角的正切值等于__.
14、如右图,半圆的直径为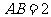 ,O为圆心,C为半圆上不同A、B的任意一点,若P为半径OC上的动点,则
,O为圆心,C为半圆上不同A、B的任意一点,若P为半径OC上的动点,则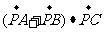 的最小值是_______.
的最小值是_______.
13、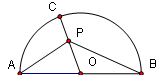 已知有序实数对(a,b)满足
已知有序实数对(a,b)满足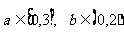 ,则关于x 的一元二次方程
,则关于x 的一元二次方程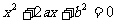 有实数根的概率是________________。
有实数根的概率是________________。
12、已知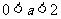 ,复数
,复数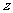 的实部为
的实部为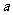 ,虚部为1,则
,虚部为1,则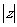 的取值范围__________。
的取值范围__________。
11、若命题“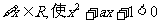 ”是真命题,则实数
”是真命题,则实数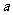 的取值范围为_____。
的取值范围为_____。
10、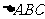 满足
满足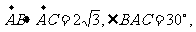 设M是
设M是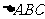 内的一点(不在边界上),定义
内的一点(不在边界上),定义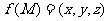 ,其中
,其中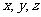 分别为
分别为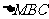 ,
,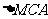 ,
,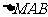 的面积,若
的面积,若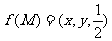 ,则
,则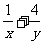 的最小值为----------------------------------
( )
的最小值为----------------------------------
( )
A.8 B.9 C.16 D.18
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com