
22. (本小题满分12分)
已知数列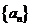 中,
中, (
(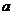 为常数),
为常数),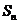 为
为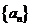 的前
的前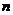 项和,且
项和,且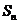 是
是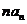 与
与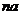 的等差中项.
的等差中项.
(Ⅰ)求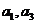 ;
;
(Ⅱ)求数列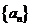 的通项公式;
的通项公式;
(Ⅲ)若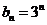 且
且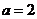 ,
,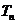 为数列
为数列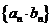 的前
的前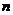 项和,求
项和,求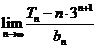 的值.
的值.
解:(1)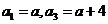 ;(2)
;(2)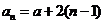 ,数学归纳法证明;
,数学归纳法证明;
(3)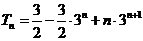 ,
,
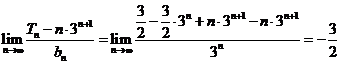
21.(本小题满分12分)
在数列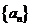 中,已知
中,已知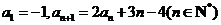
(Ⅰ)求证:数列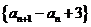 是等比数列;
是等比数列;
(Ⅱ)求数列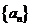 的通项公式;
的通项公式;
(Ⅲ)求数列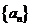 的前
的前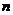 项和
项和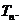
解:(2)
(3)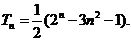
19. (本小题满分12分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有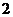 人,会跳舞的
人,会跳舞的
有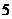 人,现从中任选
人,现从中任选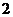 人.设
人.设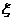 为选出的人中既会唱歌又会跳舞的人数,
为选出的人中既会唱歌又会跳舞的人数,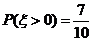 .
.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出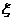 的概率分布列并计算
的概率分布列并计算 .
.
解:设既会唱歌又会跳舞的有 人,则文娱队中共有
人,则文娱队中共有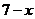 人,那么只会一项的人数是
人,那么只会一项的人数是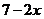 人.
人.
(Ⅰ)∵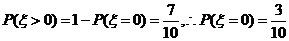
∴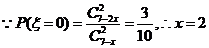
故文娱队共有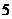 人.
人.
(Ⅱ)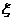 的概率分布列为
的概率分布列为
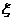
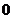
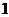
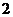
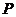
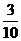
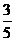
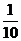
∴ 20. (本小题满分12分)
20. (本小题满分12分)
用黄、蓝、白三种颜色粉刷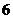 间办公室
间办公室
(Ⅰ) 若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷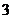 间,一种颜色粉刷
间,一种颜色粉刷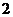 间,一种颜色粉刷
间,一种颜色粉刷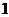 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这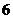 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?
解:(1)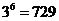 ;(2)
;(2)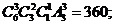
(3)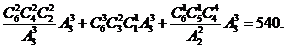
18.(本小题满分12分)
已知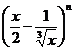 各项展开式的二项式系数之和为
各项展开式的二项式系数之和为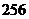 .
.
(Ⅰ)求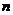 ;
;
(Ⅱ)求展开式的常数项.
解:(1)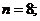 (2)
(2)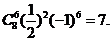
算步骤.(将答题过程写在答题纸相应位置)
17. (本小题满分10分)
求下列各式的极限值:
(Ⅰ)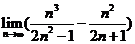 ; (Ⅱ)
; (Ⅱ)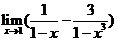 .
.
解:(1)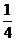 ;(2)
;(2)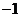 。
。
16. 给出下列命题:
①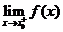 存在,且
存在,且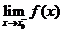 也存在,则
也存在,则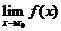 存在;
存在;
②若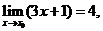 则
则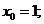
③若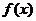 是偶函数,且
是偶函数,且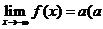 为常数),则
为常数),则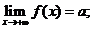
④若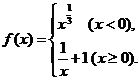 ,则
,则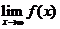 不存在.
不存在.
其中正确命题的序号是 ②③④
15.已知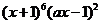 的展开式中
的展开式中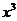 项的系数为
项的系数为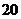 ,则实数
,则实数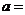
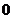 或
或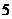
14.口袋内有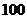 个大小相同的红球、白球和黑球,其中有
个大小相同的红球、白球和黑球,其中有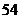 个红球,从中摸出1个球,摸出白球的概率为
个红球,从中摸出1个球,摸出白球的概率为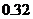 ,则摸出黑球的概率为
,则摸出黑球的概率为 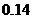
的横线上)
13. 若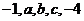 成等比数列,则
成等比数列,则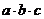 的值为
的值为 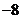
12.已知数列 满足
满足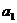 =2,
=2,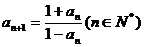 ,则
,则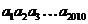 的值为.(D)
的值为.(D)
A.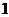 B.
B.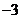 C.
C.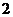 D.
D. 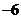
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com