
3.归纳下面这则寓言的寓意。(不超过25个字)(3分)
有一张弓做事很毛躁。一清早起来,弓张开臂,刷地就是一箭。
箭刚飞出去,弓马上就大叫起来:“唉,唉,等等,回来!我还没想好射向哪儿,你出去干什么呢!”
弓拔腿就追,可箭早没影了。
寓意:口口口口口口口口口口口口口口口口口口口口口口口口口
2.下面这段文字中,包含了许嘉璐怎样的观点?请用简洁的语言加以概括。(6分)
“现在大家都听哼哼唧唧不知所云的歌曲,久而久之会把淳朴的孩子也变得麻木,也变得不知道何为美!长此以往,我们的文化发展让人忧虑!”全国人大常委会副委员长许嘉璐是在4月18日北大召开的一次国际性会议上说这番话的,并呼吁全社会要加大保护非物质文化的力度,重视原生态文化。他介绍,自人类进入现代社会以来,随着技术的发展,文化和其他的产品一样慢慢被规范化、标准化、批量化和自动化,不断的功利性创作造成文化的浮躁,经得起历史洗涤的艺术精品却越来越少。许嘉璐认为,原生态文化对于任何民族都极其珍贵,其含括的意义十分丰富,不仅仅是表演。他强调,原生态的文化必须不断创新,使其适应变化,只有既保持传统又具备创新活力,文化才能长盛不衰。这不仅仅是对国家的贡献,也是对世界,对人类的贡献。 (取材自2006年4月24日《中国青年报》)
(1) (10个字以内)
(2) (12个字以内)
20.本题主要考查二次函数的基本性质、不等式的基本性质与解法,以及综合运用所学知识分析和解决问题的能力。满分 14分。
证明:(Ⅰ)若 a = 0, 则 b = -c ,
f (0) f (1) = c (3a + 2b + c ) 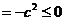 ,与已知矛盾, 所以 a ≠ 0.
,与已知矛盾, 所以 a ≠ 0.
方程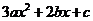 = 0 的判别式
= 0 的判别式 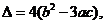 由条件 a + b + c = 0,消去 b,得
由条件 a + b + c = 0,消去 b,得
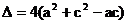
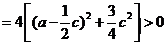 故方程 f (x) = 0 有实根.
(Ⅱ)由
故方程 f (x) = 0 有实根.
(Ⅱ)由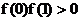 ,可知
,可知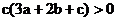
又a + b + c = 0,所以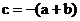
所以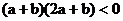 ,又a ≠ 0. 所以
,又a ≠ 0. 所以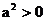
所以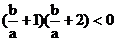 ,解得
,解得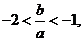
(Ⅲ)由条件,知
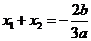 ,
, 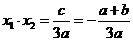 ,
,
所以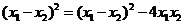
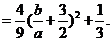 因为
因为 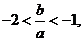 所以
所以 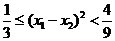
故 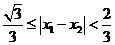
19.解法1:(Ⅰ)令g(x)=f(x)-x=x2+(a-1)x+a,则由题意可得
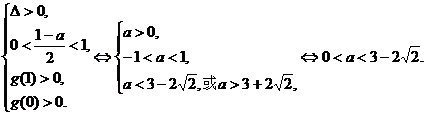
故所求实数a的取值范围是(0,3-2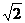 ).
).
(Ⅱ)f(0),f(1)-f(0)=g(0)g(1)=2a2, 令h(a)=2a2.
∵当a>0时h(a)单调增加,
∴当0<a<3-2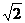 时
时
0<h(a)<h(3-2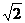 )=2(3-2
)=2(3-2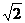 )2=2(17-12
)2=2(17-12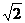 )=2·
)=2·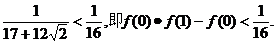
解法2:(Ⅰ)同解法1.
(Ⅱ)∵f(0)f(1)-f(0)=g(0)g(1)=2a2,由(Ⅰ)知0<a<3-2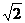
∴4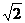 a-1<12
a-1<12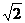 -17<0,又4
-17<0,又4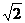 a+1>0,于是
a+1>0,于是
2a2-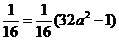 =
=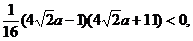
即2a2-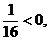 故f(0)f(1)-f(0)<
故f(0)f(1)-f(0)<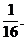
解法3:(Ⅰ)方程f(x)-x=0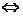 x2+(a-1)x+a=0,由韦达定理得
x2+(a-1)x+a=0,由韦达定理得
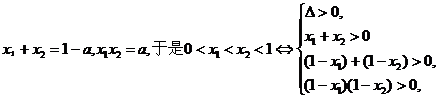
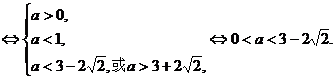
故所求实数a的取值范围是(0,3-2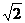 )
)
(Ⅱ)依题意可设g(x)=(x-x1)(x-x2),则由0<x1<x2<1得
f(0)f(1)-f(0)=g(0)g(1)=x1x2(1-x1)(1-x2)=[x1(1-x1)][x2(1-x2)]
<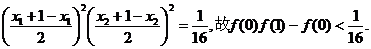
18.解: (1) 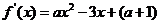 ,由于函数
,由于函数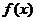 在
在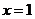 时取得极值,所以
时取得极值,所以 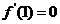
即 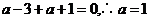
(2) 方法一:由题设知: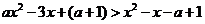 对任意
对任意 都成立
都成立
即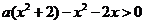 对任意
对任意 都成立
都成立
设 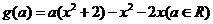 , 则对任意
, 则对任意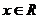 ,
,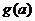 为单调递增函数
为单调递增函数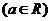
所以对任意 ,
,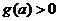 恒成立的充分必要条件是
恒成立的充分必要条件是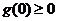
即 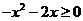 ,
,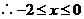
于是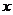 的取值范围是
的取值范围是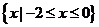
方法二:由题设知: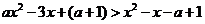 对任意
对任意 都成立
都成立
即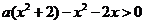 对任意
对任意 都成立
都成立
于是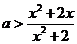 对任意
对任意 都成立,即
都成立,即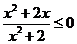
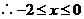
于是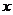 的取值范围是
的取值范围是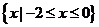
17.. 解:由f(x)为二次函数知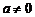
令f(x)=0解得其两根为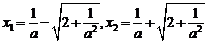
由此可知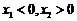
(i)当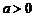 时,
时,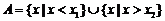
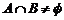 的充要条件是
的充要条件是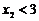 ,即
,即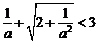 解得
解得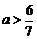
(ii)当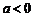 时,
时,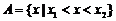
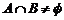 的充要条件是
的充要条件是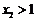 ,即
,即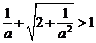 解得
解得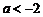
综上,使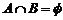 成立的a的取值范围为
成立的a的取值范围为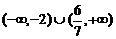
16.本小题主要考查把实际问题抽象为数学问题,应用不等式等基础知识和方法解决问题的
能力. 满分12分.
解:设矩形温室的左侧边长为a m,后侧边长为b m,则
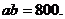
蔬菜的种植面积
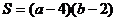
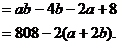
所以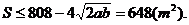
当
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最
大种植面积为648m2.
15.解:(I)由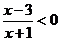 ,得
,得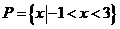 .
.
(II)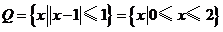 .
.
由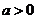 ,得
,得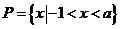 ,又
,又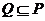 ,所以
,所以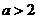 ,
,
即 的取值范围是
的取值范围是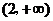 .
.
6. 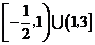 7.
7. 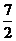 8. (0,-2) 9.14 10. 31.2万元 11.
8. (0,-2) 9.14 10. 31.2万元 11. 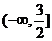 ; 12.
; 12. 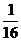 ; 13。
; 13。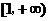 ; 14. 27
; 14. 27
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com