
1.下列哪种情况中可将物体看成质点( )。
A.研究某同学骑车回校的速度
B.对你自己骑车的姿势进行生理学分析
C.研究火星探测器从地球到火星的飞行轨迹
D.研究火星探测器降落火星后如何探测火星的表面
22. (本题满分12分)
设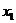 、
、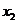
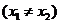 是函数
是函数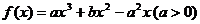 的两个极值点.
的两个极值点.
(1)若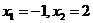 ,求函数
,求函数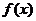 的解析式;
的解析式;
(2)若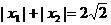 ,求
,求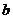 的最大值;
的最大值;
(3)设函数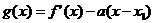 ,
,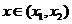 ,当
,当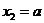 时,
时,
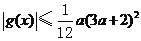 求证:
求证:
银川二中2011届月考(一)试题
21. (本题12分)
设函数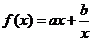 ,曲线
,曲线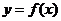 在点M
在点M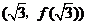 处的切线方程为
处的切线方程为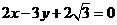 .
.
(1)求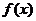 的解析式; (2)求函数
的解析式; (2)求函数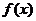 的单调递减区间;
的单调递减区间;
(3)证明:曲线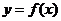 上任一点处的切线与直线
上任一点处的切线与直线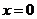 和直线
和直线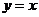 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
20.(本题12分)
已知函数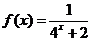
(1)证明:函数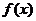 关于点
关于点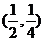 对称.
对称.
(2)求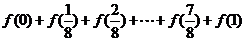 的值.
的值.
19.(本题12分)
火车站有某公司等待运送的甲种货物1530吨,乙种货物1150吨。现计划用A、B两种型号的车厢共50节运送这批货物。已知35吨甲种货物和15吨乙种货物可装满一节A型车厢;25吨甲种货物和35吨乙种货物可装满一节B型车厢。
(Ⅰ)请你根据以上条件,安排A、B两种型号的车厢的节数,列出所有可能的方案;
(Ⅱ)若每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元,哪种方案的运费最少?请你说明理由.

18. (本题12分)
已知函数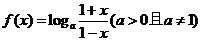
(1)求函数的定义域;
(2)判断函数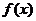 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(3)求使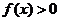 时的x取值范围.
时的x取值范围.
17.(本题10分)
若不等式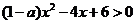 的解集是
的解集是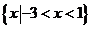 .
.
(1)解不等式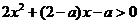 ;
;
(2)b为何值时,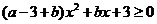 的解集R
的解集R
16.由命题“Rt ABC中,两直角边分别为a,b,斜边上的高为h,则得
ABC中,两直角边分别为a,b,斜边上的高为h,则得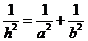 ”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
15. 已知函数
已知函数 是奇函数,它们的
是奇函数,它们的
定域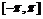 ,且它们在
,且它们在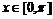 上的图象如图所示,
上的图象如图所示,
则不等式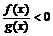 的解集是
.
的解集是
.
14.已知函数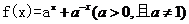 且
且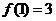 ,则
,则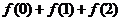 的值是__
的值是__
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com