
30、(2007全国一 理20)
设函数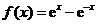 .
.
(Ⅰ)证明: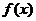 的导数
的导数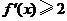 ;
;
(Ⅱ)若对所有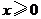 都有
都有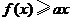 ,求
,求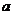 的取值范围.
的取值范围.
29、(2007湖北理 20)
已知定义在正实数集上的函数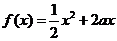 ,
, ,其中
,其中 .设两曲线
.设两曲线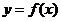 ,
,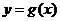 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用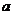 表示
表示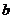 ,并求
,并求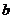 的最大值;
的最大值;
(II)求证: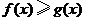 (
(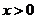 ).
).
28、(2007海南理 21)
设函数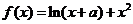
(I)若当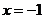 时,
时,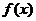 取得极值,求
取得极值,求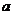 的值,并讨论
的值,并讨论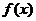 的单调性;
的单调性;
(II)若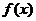 存在极值,求
存在极值,求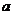 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于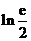 .
.
27、(2007广东理、文 20)
已知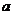 是实数,函数
是实数,函数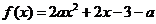 .如果函数
.如果函数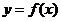 在区间
在区间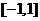 上
上
零点,求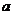 的取值范围.
的取值范围.
26、(2007福建理 22)
已知函数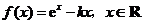
(Ⅰ)若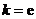 ,试确定函数
,试确定函数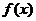 的单调区间;
的单调区间;
(Ⅱ)若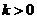 ,且对于任意
,且对于任意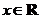 ,
,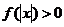 恒成立,试确定实数
恒成立,试确定实数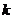 的取值范围;
的取值范围;
(Ⅲ)设函数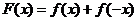 ,求证:
,求证: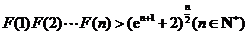 .
.
25、(2007安徽理 18)
设a≥0,f (x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F(x)在(0.+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x-2a ln x+1.
24、 (2006重庆卷)
已知函数f(x)=(x2+bx+c)cx,其中b,c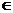 R为常数.
R为常数.
(Ⅰ)若b2>4(a-1),讨论函数f(x)的单调性;
(Ⅱ)若b2<4(c-1),且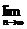
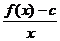 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
23、(2006浙江卷)
已知函数f(x)=x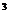 + x
+ x ,数列|x
,数列|x |(x
|(x >0)的第一项x
>0)的第一项x =1,以后各项按如下方式取定:曲线x=f(x)在
=1,以后各项按如下方式取定:曲线x=f(x)在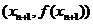 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x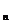 ,f (x
,f (x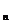 ))两点的直线平行(如图)求证:当n
))两点的直线平行(如图)求证:当n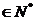 时,
时,
(Ⅰ)x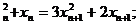
(Ⅱ)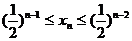
22、(2006天津卷)
已知函数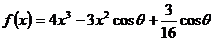 ,其中
,其中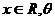 为参数,且
为参数,且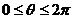 .
.
(1)当时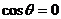 ,判断函数
,判断函数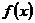 是否有极值;
是否有极值;
(2)要使函数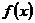 的极小值大于零,求参数
的极小值大于零,求参数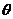 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数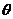 ,函数
,函数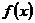 在区间
在区间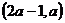 内都是增函数,求实数
内都是增函数,求实数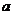 的取值范围.
的取值范围.
21、(2006四川卷)
已知函数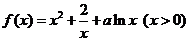 ,
,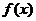 的导数是
的导数是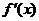 。对任意两个不等的正数
。对任意两个不等的正数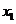 、
、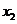 ,证明:
,证明:
(Ⅰ)当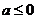 时,
时,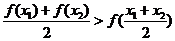 ;
;
(Ⅱ)当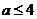 时,
时,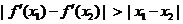 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com