
41、(2008北京卷18).
已知函数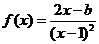 ,求导函数
,求导函数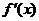 ,并确定
,并确定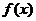 的单调区间.
的单调区间.
40.(2008全国二22).
设函数 .
.
(Ⅰ)求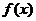 的单调区间;
的单调区间;
(Ⅱ)如果对任何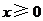 ,都有
,都有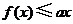 ,求
,求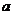 的取值范围.
的取值范围.
39、(2008全国一19).
已知函数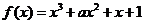 ,
,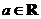 .
.
(Ⅰ)讨论函数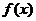 的单调区间;
的单调区间;
(Ⅱ)设函数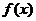 在区间
在区间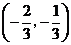 内是减函数,求
内是减函数,求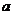 的取值范围.
的取值范围.
38、(2007重庆理 20)
已知函数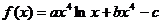 (x>0)在x = 1处取得极值--3--c,其中a,b,c为常数。
(x>0)在x = 1处取得极值--3--c,其中a,b,c为常数。
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式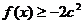 恒成立,求c的取值范围。
恒成立,求c的取值范围。
37、(2007浙江理 22)
设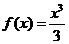 ,对任意实数
,对任意实数 ,记
,记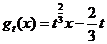 .
.
(I)求函数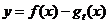 的单调区间;
的单调区间;
(II)求证:(ⅰ)当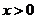 时,
时,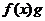
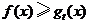 对任意正实数
对任意正实数 成立;
成立;
(ⅱ)有且仅有一个正实数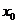 ,使得
,使得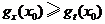 对任意正实数
对任意正实数 成立.
成立.
36、(2007四川理 22)
设函数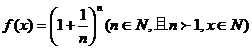 .
.
(Ⅰ)当x=6时,求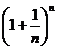 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明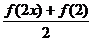 >
>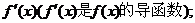
(Ⅲ)是否存在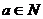 ,使得an<
,使得an<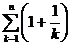 <
<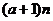 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
35、(2007上海理科19)
已知函数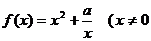 ,常数
,常数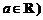 .
.
(1)讨论函数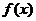 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数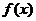 在
在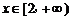 上为增函数,求
上为增函数,求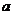 的取值范围.
的取值范围.
34、(2007陕西理 20)
设函数f(x)=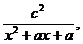 其中a为实数.
其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时,求f(x)的单减区间.
32、(2007山东理 22)
设函数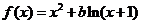 ,其中
,其中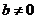 .
.
(Ⅰ)当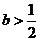 时,判断函数
时,判断函数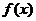 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数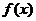 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数 ,不等式
,不等式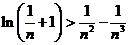 都成立.
都成立.
33(2007山东文 21)
设函数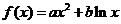 ,其中
,其中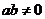 .
.
证明:当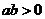 时,函数
时,函数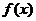 没有极值点;当
没有极值点;当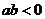 时,函数
时,函数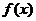 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
31、(2007全国二理 22)
已知函数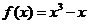 .
.
(1)求曲线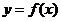 在点
在点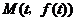 处的切线方程;
处的切线方程;
(2)设 ,如果过点
,如果过点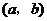 可作曲线
可作曲线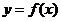 的三条切线,证明:
的三条切线,证明: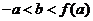 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com