
4.一质点沿直线Ox方向做变速运动,它离开O点的距离x随时间变化的关系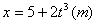 ,它的速度随时间t变化的关系为v=6t2(m/s),该质点在t=0到t=2s间的平均速度和t=2s到t=3s间的平均速度的大小分别为 ( )
,它的速度随时间t变化的关系为v=6t2(m/s),该质点在t=0到t=2s间的平均速度和t=2s到t=3s间的平均速度的大小分别为 ( )
A.12m/s,39m/s B.8m/s,38m/s
C.12m/s,19.5m/s D.8m/s,13m/s
3.如图A、B两物体叠放在一起,用手托住,让它们静靠在竖直墙边,然后释放,它们同时沿墙面向下滑,已知mA>mB,则物体B ( )
 A.只受一个重力
A.只受一个重力
B.受到重力和一个摩擦力
C.受到重力、一个弹力和一个摩擦力
D.受到重力、一个摩擦力和两个弹力
2.从某一高度相隔1s释放两个相同的小球甲和乙,不计空气阻力,它们在空中任一时刻( )
A.甲、乙两球距离越来越大,甲、乙两球速度之差越来越大
B.甲、乙两球距离始终保持不变,甲、乙两球速度之差保持不变
C.甲、乙两球距离越来越大,但甲、乙两球速度之差保持不变
D.甲、乙两球距离越来越小,甲、乙两球速度之差越来越小
1.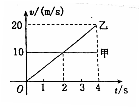 甲、乙两个质点同时、同地向同一方向做直线运动,它们的速度一时间图象如右图所示,则由图象可知( )
甲、乙两个质点同时、同地向同一方向做直线运动,它们的速度一时间图象如右图所示,则由图象可知( )
A.甲质点比乙质点运动得快,故乙追不上甲
B.在2s末时乙追上甲
C.在2s末时甲、乙的位移相同
D.甲做匀速直线运动,乙做初速度为零的匀加速直线运动
22.(本小题满分14分)
已知定义域为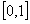 的函数
的函数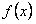 同时满足以下三个条件:
同时满足以下三个条件:
① 对任意的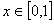 ,总有
,总有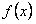 ≥0; ②
≥0; ②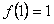
 ; ③若
; ③若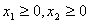 且
且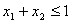 ,则有
,则有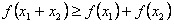 成立,并且称
成立,并且称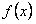 为“友谊函数”,
为“友谊函数”,
请解答下列各题:
(1)若已知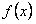 为“友谊函数”,求
为“友谊函数”,求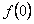 的值;
的值;
(2)函数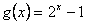 在区间
在区间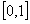 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知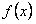 为“友谊函数”,且
为“友谊函数”,且 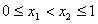 ,求证:
,求证: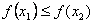
21.(本小题满分12分)
设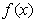 的定义域是
的定义域是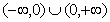 ,且
,且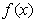 对任意不为零的实数x都满足
对任意不为零的实数x都满足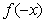 =
=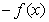 .已知当x>0时
.已知当x>0时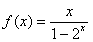
(1)求当x<0时,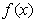 的解析式 (2)解不等式
的解析式 (2)解不等式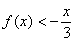 .
.
20. (本小题满分12分)已知函数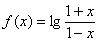
(Ⅰ)求证:对于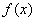 的定义域内的任意两个实数
的定义域内的任意两个实数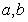 ,都有
,都有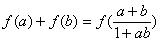 ;
;
(Ⅱ)判断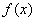 的奇偶性,并予以证明.
的奇偶性,并予以证明.
19.(本小题满分12分)
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收入满足函数:
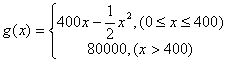 ,其中
,其中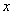 是仪器的月产量。
是仪器的月产量。
(1) 将利润表示为月产量的函数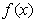 ;
;
(2) 当月产量为何值时,公司所获得的利润最大?最大利润为多少元?
18. (本小题满分12分)
设命题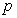 :函数
:函数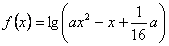 的定义域为R; 命题
的定义域为R; 命题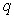 :不等式
:不等式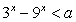 对一切正实数均成立
对一切正实数均成立
(1)如果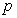 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“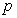 或
或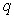 ”为真命题且“
”为真命题且“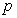 且
且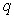 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
17.(本题满分12分)
已知集合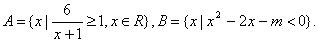
(1)当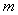 =3时,求
=3时,求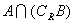 ;
;
(2)若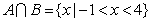 ,求实数
,求实数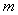 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com