
22.解: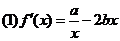 ……1分
……1分
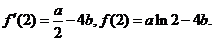
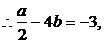 且
且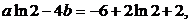
解得: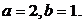 ……1分
……1分
由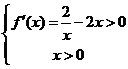 解得
解得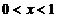
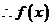 的单调增区间是
的单调增区间是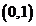 ……2分
……2分
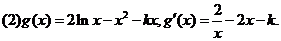 ……1分
……1分
假设结论 在
在 处取极值,则
处取极值,则 成立,则有
成立,则有
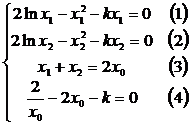
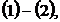 得
得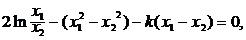

21.解:(1)椭圆方程是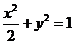 ……4分
……4分
(2)由已知条件,直线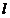 :
: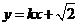 ,代入椭圆方程得
,代入椭圆方程得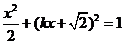 .
.
整理得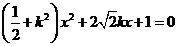 ①……2分
①……2分
由已知得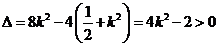 ,解得
,解得 或
或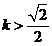 .……1分
.……1分
设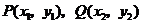 ,则
,则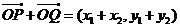 ,
,
由方程①,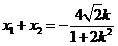 . ②
. ②
又 . ③
. ③
而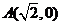 ,
,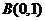 ,
,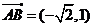 ,
,
所以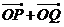 与
与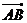 共线等价于
共线等价于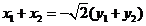 ,
,
将②③代入上式,解得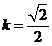 ,……4分
,……4分
又 或
或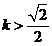 ,
,
故没有符合题意的常数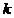 .……1分
.……1分
20.解:(1)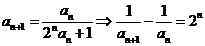 ……1分
……1分
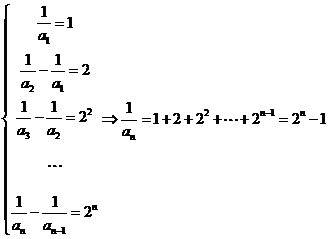 ……2分
……2分
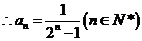 ……1分
……1分
(2)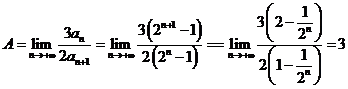 ……2分
……2分
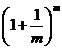 的通项
的通项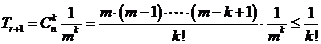 ……2分
……2分
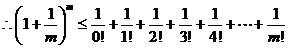

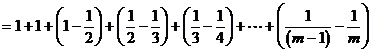
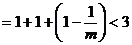
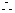 对任意
对任意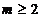 ,且
,且 ,都有
,都有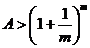 ……4分
……4分
19.解:设“科目A第一次考试合格”为事件A,“科目A补考合格”为事件A2;
“科目B第一次考试合格”为事件B,“科目B补考合格”为事件B. ……1分
(1)不需要补考就获得证书的事件为A1·B1,注意到A1与B1相互独立,
则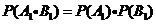
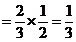 ……2分
……2分
答:该考生不需要补考就获得证书的概率为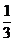 .……1分
.……1分
(2)由已知得,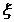 =2,3,4 ……1分
=2,3,4 ……1分
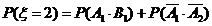 ……1分
……1分
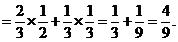 ……1分
……1分
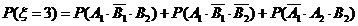
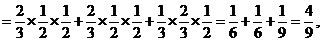 ……1分
……1分
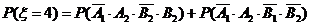
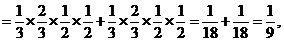 ……1分
……1分
故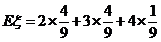
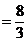 ……2分
……2分
答:该考生参加考试次数的数学期望为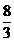 .……1分
.……1分
22.已知 图像上一点
图像上一点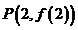 处的切线方程为
处的切线方程为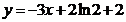 .
.
(Ⅰ)求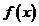 的单调增区间;
的单调增区间;
(Ⅱ)令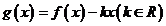 ,如果
,如果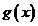 图像与
图像与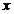 轴交于
轴交于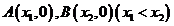 两点,
两点,
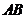 的中点为
的中点为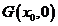 ,问
,问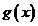 在
在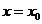 处是否取得极值.
处是否取得极值.

 四边形
四边形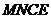 是平行四边形,……2分
是平行四边形,……2分  ……1分
……1分
(2)作 交
交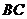 于
于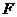 ,
,
分别以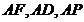 为
为 轴建立如图空间直角坐标系……1分
轴建立如图空间直角坐标系……1分
则
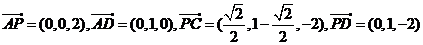
设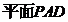 的一个法向量为
的一个法向量为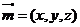

由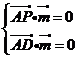 ,……1分 得
,……1分 得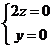 ,
, 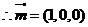 ……1分
……1分
同理求得 的一个法向量为
的一个法向量为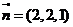 ……2分
……2分
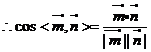
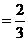 ……2分
……2分 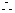 二面角
二面角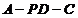 的大小为
的大小为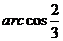 ……1分
……1分
21.已知椭圆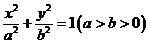 的离心率
的离心率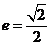 ,短轴长为
,短轴长为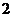 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)若椭圆与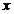 轴正半轴、
轴正半轴、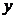 轴正半轴的交点分别为
轴正半轴的交点分别为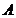 、
、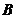 ,经过点
,经过点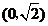 且斜率为
且斜率为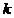 的直线
的直线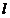 与椭圆交于不同的两点
与椭圆交于不同的两点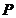 、
、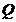 .是否存在常数
.是否存在常数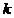 ,使得向量
,使得向量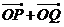 与
与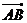 共线?如果存在,求
共线?如果存在,求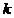 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
20.
已知数列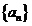 满足
满足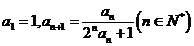 .
.
(Ⅰ)求数列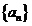 通项
通项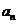 ;
;
(Ⅱ)设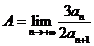 ,证明:对任意
,证明:对任意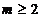 ,且
,且 ,都有
,都有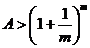 .
.
19.某项考试按科目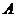 、科目
、科目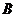 依次进行,只有当科目
依次进行,只有当科目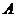 成绩合格时,才可继续参加科目
成绩合格时,才可继续参加科目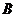 的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目
的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目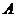 每次考试成绩合格的概率均为
每次考试成绩合格的概率均为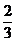 ,科目
,科目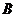 每次考试成绩合格的概率均为
每次考试成绩合格的概率均为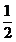 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,
,
求 的数学期望
的数学期望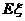 .
.
18.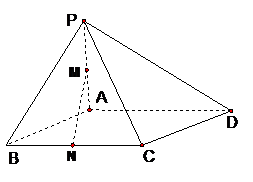 如图,在四棱锥
如图,在四棱锥 中,底面
中,底面 是边长为
是边长为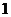 的菱形,
的菱形,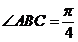 ,
, 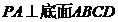 ,
,  ,
,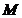 为
为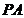 的中点,
的中点,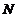 为
为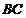 的中点.
的中点.
(Ⅰ)证明:直线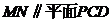 ;
;
(Ⅱ)求二面角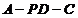 的大小.
的大小.
17. 已知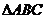 的周长为
的周长为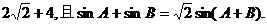
(Ⅰ)求边AB的长;
(Ⅱ)若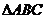 的面积
的面积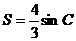 ,求角C的大小.
,求角C的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com