
题型1:共线、共点和共面问题
例1.(1)如图所示,平面ABD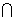 平面BCD =直线BD
,M
、N
、P
、Q
分别为线段AB
、BC
、CD
、DA
上的点,四边形MNPQ 是以PN
、QM
为腰的梯形。
平面BCD =直线BD
,M
、N
、P
、Q
分别为线段AB
、BC
、CD
、DA
上的点,四边形MNPQ 是以PN
、QM
为腰的梯形。
试证明三直线BD 、MQ 、NP 共点。
证明:∵ 四边形MNPQ 是梯形,且MQ 、NP 是腰,
∴直线MQ 、NP 必相交于某一点O 。
∵ O  直线MQ ;直线MQ
直线MQ ;直线MQ
 平面ABD ,
平面ABD ,
∴ O  平面ABD。
平面ABD。
同理,O 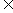 平面BCD ,又两平面ABD 、BCD 的交线为BD
,
平面BCD ,又两平面ABD 、BCD 的交线为BD
,
故由公理二知,O 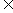 直线BD ,从而三直线BD
、MQ
、NP
共点。
直线BD ,从而三直线BD
、MQ
、NP
共点。
点评:由已知条件,直线MQ 、NP 必相交于一点O ,因此,问题转化为求证点O 在直线BD 上,由公理二,就是要寻找两个平面,使直线BD 是这两个平面的交线,同时点O 是这两个平面的公共点即可.“三点共线”及“三线共点”的问题都可以转化为证明“点在直线上”的问题。
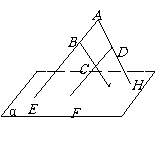 (2)如图所示,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线
(2)如图所示,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线
证明:∵AB∥CD,
∴AB,CD确定一个平面β.
又∵AB α=E,AB
α=E,AB β,∴E∈α,E∈β,
β,∴E∈α,E∈β,
即E为平面α与β的一个公共点。
同理可证F,G,H均为平面α与β的公共点.
∵两个平面有公共点,它们有且只有一条通过公共点的公共直线,
∴E,F,G,H四点必定共线。
点评:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论。
例2.已知:a,b,c,d是不共点且两两相交的四条直线,求证:a,b,c,d共面。
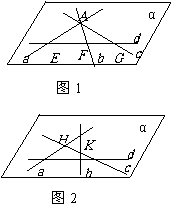
证明:1o若当四条直线中有三条相交于一点,不妨设a,b,c相交于一点A,
但AÏd,如图1所示:
∴直线d和A确定一个平面α。
 又设直线d与a,b,c分别相交于E,F,G,
又设直线d与a,b,c分别相交于E,F,G,
则A,E,F,G∈α。
∵A,E∈α,A,E∈a,∴a α。
α。
同理可证b α,c
α,c α。
α。
∴a,b,c,d在同一平面α内。
2o当四条直线中任何三条都不共点时,
如图2所示:
∵这四条直线两两相交,则设相交直线a,b确定一个平面α。
设直线c与a,b分别交于点H,K,则H,K∈α。
又 H,K∈c,∴c,则c α。
α。
同理可证d α。
α。
∴a,b,c,d四条直线在同一平面α内.
点评:证明若干条线(或若干个点)共面的一般步骤是:首先根据公理3或推论,由题给条件中的部分线(或点)确定一个平面,然后再根据公理1证明其余的线(或点)均在这个平面内。本题最容易忽视“三线共点”这一种情况。因此,在分析题意时,应仔细推敲问题中每一句话的含义。
题型2:异面直线的判定与应用
例3.已知:如图所示,a 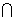 b =a
,b
b =a
,b
 b ,a
b ,a
 b
=A
,c
b
=A
,c
 a ,c
∥a
。求证直线b
、c
为异面直线
a ,c
∥a
。求证直线b
、c
为异面直线
证法一:假设b
、c
共面于g .由A
 a
,a
∥c
知,A
a
,a
∥c
知,A
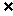 c
,而a
c
,而a
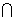 b
=A,a
b
=A,a 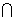 b =a
,
b =a
,
∴ A 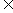 g ,A
g ,A
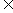 a。
a。
又c
 a ,∴ g 、a 都经过直线c
及其外的一点A,
a ,∴ g 、a 都经过直线c
及其外的一点A,
∴ g 与a 重合,于是a
 g ,又b
g ,又b
 b。
b。
又g 、b 都经过两相交直线a 、b ,从而g 、b 重合。
∴ a 、b 、g 为同一平面,这与a 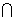 b =a
矛盾
b =a
矛盾
∴ b 、c 为异面直线.
证法二:假设b 、c 共面,则b ,c 相交或平行。
(1)若b
∥c
,又a
∥c
,则由公理4知a
∥b
,这与a
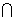 b
=A
矛盾。
b
=A
矛盾。
(2)若b
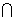 c
=P
,已知b
c
=P
,已知b
 b ,c
b ,c
 a ,则P
是a 、b 的公共点,由公理2,P
a ,则P
是a 、b 的公共点,由公理2,P
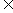 a
,又b
a
,又b
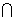 c
=P
,即P
c
=P
,即P
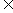 c
,故a
c
,故a
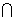 c
=P
,这与a
∥c
矛盾
c
=P
,这与a
∥c
矛盾
综合(1)、(2)可知,b 、c 为异面直线。
证法三:∵ a 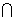 b =a
,a
b =a
,a
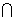 b
=A
,∴ A
b
=A
,∴ A 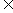 a
。
a
。
∵ a ∥c ,∴ A
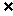 c
,
c
,
在直线b
上任取一点P(P 异于A),则P 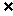 a(否则b
a(否则b  a ,又a
a ,又a
 a ,则a 、b 都经过两相交直线a
、b
,则a 、b 重合,与a
a ,则a 、b 都经过两相交直线a
、b
,则a 、b 重合,与a 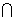 b =a
矛盾)。
b =a
矛盾)。
又c  a ,于是根据“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线”知,b
、c
为异面直线。
a ,于是根据“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线”知,b
、c
为异面直线。
点评:证明两直线为异面直线的思路主要有两条:一是利用反证法;二是利用结论“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.。异面直线又有两条途径:其一是直接假设b 、c 共面而产生矛盾;其二是假设b 、c 平行与相交;分别产生矛盾。判定直线异面,若为解答题,则用得最多的是证法一、二的思路;若为选择或填空题,则往往都是用证法三的思路。用反证法证题,一般可归纳为四个步骤:(1)否定结论;(2)进行推理;(3)导出矛盾;(4)肯定结论.
宜用反证法证明的命题往往是(1)基本定理或某一知识系统的初始阶段的命题(如立体几何中的线面、面面平行的判定定量的证明等);(2)肯定或否定型的命题(如结论中出现“必有”、“必不存在”等一类命题);(3)唯一型的命题(如“图形唯一”、“方程解唯一”等一类命题);(4)正面情况较为繁多,而结论的反面却只有一两种情况的一类命题;(5)结论中出现“至多”、“不多于”等一类命题。
例4.(1)已知异面直线a,b所成的角为70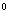 ,则过空间一定点O,与两条异面直线a,b都成60
,则过空间一定点O,与两条异面直线a,b都成60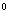 角的直线有( )条
角的直线有( )条
A.1 B.2 C.3 D.4
(2)异面直线a,b所成的角为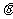 ,空间中有一定点O,过点O有3条直线与a,b所成角都是60
,空间中有一定点O,过点O有3条直线与a,b所成角都是60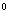 ,则
,则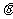 的取值可能是( )
的取值可能是( )
A.30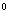 B.50
B.50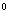 C.60
C.60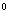 D.90
D.90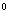
解析:(1)过空间一点O分别作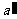 ∥a,
∥a,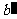 ∥b。
∥b。
将两对对顶角的平分线绕O点分别在竖直平面内转动,总能得到与 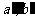 都成60
都成60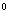 角的直线。故过点 O与a,b都成60
角的直线。故过点 O与a,b都成60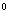 角的直线有4条,从而选D。
角的直线有4条,从而选D。
(2)过点O分别作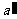 ∥a、
∥a、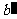 ∥b,则过点O有三条直线与a,b所成角都为60
∥b,则过点O有三条直线与a,b所成角都为60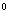 ,等价于过点O有三条直线与
,等价于过点O有三条直线与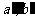 所成角都为60
所成角都为60 ,其中一条正是
,其中一条正是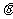 角的平分线。从而可得选项为C。
角的平分线。从而可得选项为C。
点评:该题以学生对异面直线所成的角会适当转化,较好的考察了空间想象能力
题型3:线线平行的判定与性质
例5.(2009江苏卷)设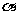 和
和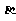 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若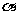 内的两条相交直线分别平行于
内的两条相交直线分别平行于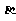 内的两条直线,则
内的两条直线,则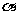 平行于
平行于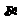 ;
;
(2)若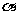 外一条直线
外一条直线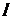 与
与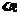 内的一条直线平行,则
内的一条直线平行,则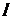 和
和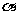 平行;
平行;
(3)设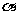 和
和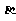 相交于直线
相交于直线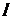 ,若
,若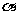 内有一条直线垂直于
内有一条直线垂直于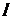 ,则
,则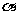 和
和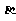 垂直;
垂直;
(4)直线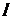 与
与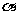 垂直的充分必要条件是
垂直的充分必要条件是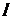 与
与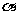 内的两条直线垂直。
内的两条直线垂直。
上面命题中,真命题的序号
(写出所有真命题的序号). 
[解析] 考查立体几何中的直线、平面的垂直与平行判定的相关定理。
真命题的序号是(1)(2)
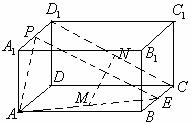
例6.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE。
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB。
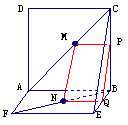 ∴MP∥NQ,又AM=NF,AC=BF,
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE。
证法二:如图过M作MH⊥AB于H,则MH∥BC,
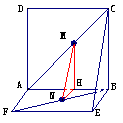 ∴
∴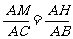
连结NH,由BF=AC,FN=AM,得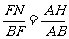
∴ NH//AF//BE
由MH//BC, NH//BE得:平面MNH//平面BCE
 ∴MN∥平面BCE
∴MN∥平面BCE 。
。
题型4:线面平行的判定与性质
例7.(2009山东卷理)(本小题满分12分)
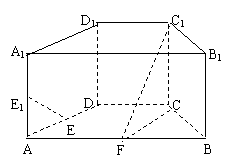 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2, AA =2, E、E
=2, E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(1) 证明:直线EE //平面FCC
//平面FCC ;
;
(2) 求二面角B-FC -C的余弦值。
-C的余弦值。 

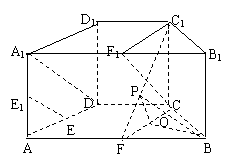 解法一:(1)在直四棱柱ABCD-A
解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为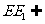 平面FCC
平面FCC ,
,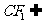 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角,
在△BCF为正三角形中,
-C的一个平面角,
在△BCF为正三角形中,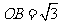 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵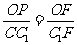 ∴
∴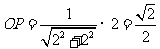 ,
, 

在Rt△OPF中,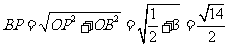 ,
,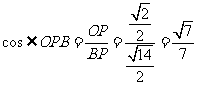 ,所以二面角B-FC
,所以二面角B-FC -C的余弦值为
-C的余弦值为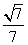 .
.
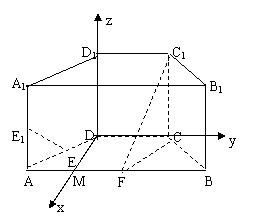 解法二:(1)因为AB=4,
BC=CD=2, F是棱AB的中点,
解法二:(1)因为AB=4,
BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
,则D(0,0,0),A(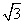 ,-1,0),F(
,-1,0),F(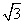 ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E(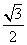 ,
,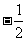 ,0),E1(
,0),E1(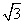 ,-1,1),所以
,-1,1),所以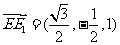 ,
,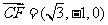 ,
,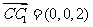
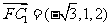 设平面CC1F的法向量为
设平面CC1F的法向量为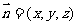 则
则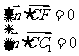 所以
所以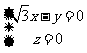 取
取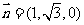 ,则
,则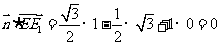 ,所以
,所以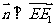 ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
. 

(2)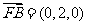 ,设平面BFC1的法向量为
,设平面BFC1的法向量为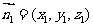 ,则
,则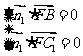 所以
所以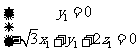 ,取
,取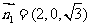 ,则
,则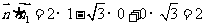 ,
,
 ,
,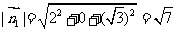 ,
, 

所以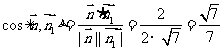 ,由图可知二面角B-FC
,由图可知二面角B-FC -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC -C的余弦值为
-C的余弦值为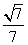 .
. 

[命题立意]:本题主要考查直棱柱的概念、线面位置关系的判定和二面角的计算.考查空间想象能力和推理运算能力,以及应用向量知识解答问题的能力.
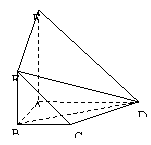
例8.(2008四川 19,理21)
(本小题满分12分)
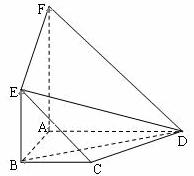
如图,平面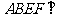 平面
平面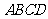 ,四边形
,四边形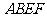 与
与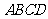 都是直角梯形,
都是直角梯形,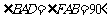 ,
,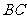 ∥
∥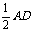 ,
,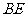 ∥
∥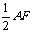 .
.
(Ⅰ)证明: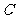 、
、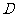 、
、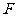 、
、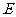 四点共面;
四点共面;
(Ⅱ)设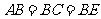 ,求二面角
,求二面角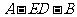 的大小.
的大小.
解析:不是会不会的问题,而是熟不熟的问题,答题时间是最大问题.
(Ⅰ)∵面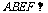 面
面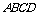 ,
,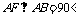
∴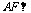 面
面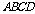 .
.
∴以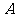 为原点,以
为原点,以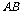 ,
,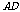 ,
,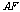 所在直线为
所在直线为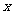 轴,
轴,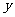 轴,
轴,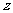 轴,
轴,
建立如图所示的空间直角坐标系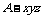 .
.
不妨设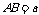 ,
,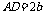 ,
,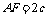 ,则
,则
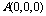 ,
,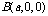 ,
,
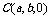 ,
,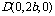 ,
,
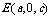 ,
,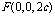 .
.
∴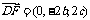 ,
,
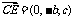 ,
,
∴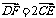 ,
,
∴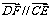 ,
,
∵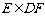 ,∴
,∴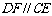 ,∴C、D、E、F四点共面.
,∴C、D、E、F四点共面.
(Ⅱ)设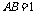 ,则
,则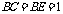 ,
,
∴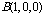 ,
,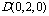 ,
,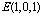 .
.
设平面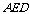 的法向量为
的法向量为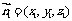 ,
,
由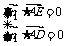 ,得
,得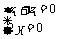 ,
,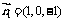
设平面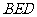 的法向量为
的法向量为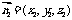
由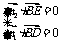 ,得
,得 ,
,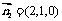
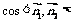
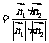
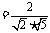
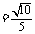
由图知,二面角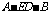 为锐角,
为锐角,
∴其大小为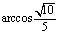 .
.
点评:证共面就是证平行,求二面角转为求法向量夹角,时间问题是本题的困惑处.心浮气燥会在计算、书写、时间上丢分.因建系容易,提倡用向量法.本时耗时要超过17题与18题用时之和.
题型5:面面平行的判定与性质
例9.如图,正方体ABCD-A1B1C1D1 的棱长为a。证明:平面ACD1 ∥平面A1C1B 。
证明:如图,∵ A1BCD1 是矩形,A1B ∥D1C 。
又D1C  平面D1CA ,A1B
平面D1CA ,A1B  平面D1CA ,
平面D1CA ,
∴ A1B ∥平面D1CA。
同理A1C1 ∥平面D1CA ,又A1C1 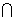 A1B =A1 ,∴ 平面D1CA ∥平面BA1C1 .
A1B =A1 ,∴ 平面D1CA ∥平面BA1C1 .
点评:证明面面平行,关键在于证明A1C1 与A1B 两相交直线分别与平面ACD1 平行。
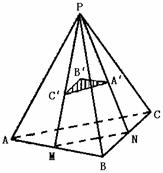 例10.P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PCA、△PAB的重心。
例10.P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PCA、△PAB的重心。
(1)求证:平面A′B′C′∥平面ABC;
(2)S△A′B′C′∶S△ABC的值。
解析:(1)取AB、BC的中点M、N,
则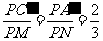
∴A′C′∥MN?A′C′∥平面ABC。
同理A′B′∥面ABC,
∴△A′B′C′∥面ABC.
(2)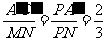
 A′C′=
A′C′=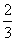 MN=
MN=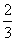 ·
·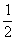 AC=
AC=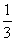 AC
AC
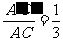 ,
,
同理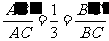
∴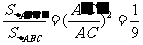
5.两个平面的位置关系有两种:两平面相交(有一条公共直线)、两平面平行(没有公共点)
 (1)两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于一个平面,那么这两个平面平行。
(1)两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于一个平面,那么这两个平面平行。
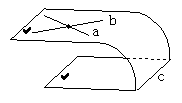 定理的模式:
定理的模式: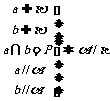
推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面互相平行。
推论模式: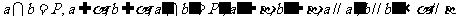
(2)两个平面平行的性质(1)如果两个平面平行,那么其中一个平面内的直线平行于另一个平面;(2)如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
4.直线和平面的位置关系
(1)直线在平面内(无数个公共点);
(2)直线和平面相交(有且只有一个公共点);
(3)直线和平面平行(没有公共点)--用两分法进行两次分类。
它们的图形分别可表示为如下,符号分别可表示为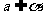 ,
,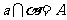 ,
,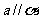 。
。
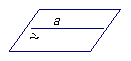
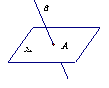
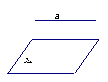
线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。推理模式: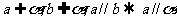 .
.

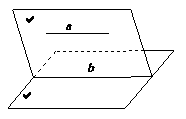 线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行
线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行
推理模式: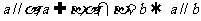 .
.
3.空间直线:
(1)空间两条直线的位置关系:
相交直线--有且仅有一个公共点;
平行直线--在同一平面内,没有公共点;
异面直线--不同在任何一个平面内,没有公共点。相交直线和平行直线也称为共面直线。
异面直线的画法常用的有下列三种:
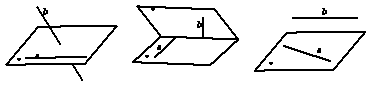
(2)平行直线:
在平面几何中,平行于同一条直线的两条直线互相平行,这个结论在空间也是成立的。即公理4:平行于同一条直线的两条直线互相平行。
(3)异面直线定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线。推理模式: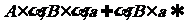
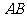 与a是异面直线。
与a是异面直线。
2.三公理三推论:
公理1:若一条直线上有两个点在一个平面内,则该直线上所有的点都在这个平面内:
A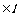 ,B
,B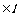 ,A
,A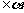 ,B
,B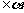

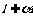
公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
公理3:经过不在同一直线上的三点,有且只有一个平面。
推论一:经过一条直线和这条直线外的一点,有且只有一个平面。
推论二:经过两条相交直线,有且只有一个平面。
推论三:经过两条平行直线,有且只有一个平面
1.平面概述
(1)平面的两个特征:①无限延展 ②平的(没有厚度)
(2)平面的画法:通常画平行四边形来表示平面
(3)平面的表示:用一个小写的希腊字母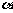 、
、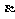 、
、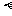 等表示,如平面
等表示,如平面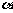 、平面
、平面 ;用表示平行四边形的两个相对顶点的字母表示,如平面AC。
;用表示平行四边形的两个相对顶点的字母表示,如平面AC。
立体几何在高考中占据重要的地位,通过近几年的高考情况分析,考察的重点及难点稳定,高考始终把直线与直线、直线与平面、平面与平面平行的性质和判定作为考察重点。在难度上也始终以中等偏难为主,在新课标教材中将立体几何要求进行了降低,重点在对图形及几何体的认识上,实现平面到空间的转化,示知识深化和拓展的重点,因而在这部分知识点上命题,将是重中之重。
预测2010年高考将以多面体为载体直接考察线面位置关系:
(1)考题将会出现一个选择题、一个填空题和一个解答题;
(2)在考题上的特点为:热点问题为平面的基本性质,考察线线、线面和面面关系的论证,此类题目将以客观题和解答题的第一步为主
2.空间中的平行关系
以立体几何的上述定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行、垂直的有关性质与判定。通过直观感知、操作确认,归纳出以下判定定理:
◆平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;
◆一个平面内的两条相交直线与另一个平面平行,则这两个平面平行;
通过直观感知、操作确认,归纳出以下性质定理,并加以证明:
◆一条直线与一个平面平行,则过该直线的任一个平面与此平面的交线与该直线平行;
◆两个平面平行,则任意一个平面与这两个平面相交所得的交线相互平行;
◆垂直于同一个平面的两条直线平行
能运用已获得的结论证明一些空间位置关系的简单命题
1.平面的基本性质与推论
借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间线、面位置关系的定义,并了解如下可以作为推理依据的公理和定理:
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内;
◆公理2:过不在一条直线上的三点,有且只有一个平面;
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;
◆公理4:平行于同一条直线的两条直线平行;
◆定理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补
2.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.
求距离的一般方法和步骤是:一作--作出表示距离的线段;二证--证明它就是所要求的距离;三算--计算其值.此外,我们还常用体积法求点到平面的距离.
求空间中线面的夹角或距离需注意以下几点:
①注意根据定义找出或作出所求的成角或距离,一般情况下,力求明确所求角或距离的位置.
②作线面角的方法除平移外,补形也是常用的方法之一;求线面角的关键是寻找两“足”(斜足与垂足),而垂足的寻找通常用到面面垂直的性质定理.
③求二面角高考中每年必考,复习时必须高度重视.二面角的平角的常用作法有三种:
根据定义或图形特征作;根据三垂线定理(或其逆定理)作,难点在于找到面的垂线.解决办法,先找面面垂直,利用面面垂直的性质定理即可找到面的垂线;作棱的垂面。作二面角的平面角应把握先找后作的原则.此外在解答题中一般不用公式“cosθ=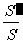 ”求二面角否则要适当扣分。
”求二面角否则要适当扣分。
④求点到平面的距离常用方法是直接法与间接法,利用直接法求距离需找到点在面内的射影,此时常考虑面面垂直的性质定理与几何图形的特殊性质.而间接法中常用的是等积法及转移法.
⑤求角与距离的关键是将空间的角与距离灵活转化为平面上的角与距离,然后将所求量置于一个三角形中,通过解三角形最终求得所需的角与距离
求距离的关键是化归。即空间距离与角向平面距离与角化归,各种具体方法如下:
(1)求空间中两点间的距离,一般转化为解直角三角形或斜三角形。
(2)求点到直线的距离和点到平面的距离,一般转化为求直角三角形斜边上的高;或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高,即用体积法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com