
1.求最大公约数
(1)短除法
求两个正整数的最大公约数的步骤:先用两个数公有的质因数连续去除,一直除到所得的商是两个互质数为止,然后把所有的除数连乘起来.
(2)穷举法(也叫枚举法)
穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数
.
(3)辗转相除法
辗转相除法求两个数的最大公约数,其算法可以描述如下:
① 输入两个正整数m和n;
② 求余数r:计算m除以n,将所得余数存放到变量r中;
③更新被除数和余数:m=n,n=r;
④判断余数r是否为0。若余数为0,则输出结果;否则转向第②步继续循环执行.
如此循环,直到得到结果为止。
(4)更相减损术
我国早期也有解决求最大公约数问题的算法,就是更相减损术。在《九章算术》中记载了更相减损术求最大公约数的步骤:可半者半之,不可半者,副置分母•子之数,以少减多,更相减损,求其等也,以等数约之.
步骤:
Ⅰ.任意给出两个正数;判断它们是否都是偶数。若是,用2约简;若不是,执行第二步。
Ⅱ.以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。继续这操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
算法是高中数学新课程中的新增内容,本讲的重点是几种重要的算法案例思想,复习时重算法的思想轻算法和程序的构造。
预测2010年高考队本讲的考察是:以选择题或填空题的形式出现,分值在5分左右,考察的热点是算法实例和传统数学知识的结合题目.
2.反证法
反证法是立体几何中常用的间接证明方法。
其步骤是:①否定结论;②进行推理;③导出矛盾;④肯定结论.用反证法证题要注意:①宜用此法否;②命题结论的反面情况有几种。
2.“升降维”思想
直线是一维的,平面是二维的,立体空间是三维的。运用降维的方法把立体空间问题转化为平面或直线问题进行研究和解题,可以化难为易,化新为旧,化未知为已知,从而使问题得到解决。运用升维的方法把平面或直线中的概念、定义或方法向空间推广,可以立易解难,温旧知新,从已知探索未知,是培养创新精神和能力,是“学会学习”的重要方法。平面图形的翻折问题的分析与解决,就是升维与降维思想方法的不断转化运用的过程。
2. 垂直转化:线线垂直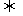 线面垂直
线面垂直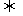 面面垂直;
面面垂直;
每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行最终达到目的。
例如:有两个平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直。
1. 平行转化:线线平行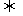 线面平行
线面平行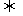 面面平行;
面面平行;
1.通过典型问题掌握基本解题方法,高考中立体几何解答题基本题型是:
(Ⅰ)证明空间线面平行或垂直;
(Ⅱ)求空间中线面的夹角或距离;
(Ⅲ)求几何体的侧面积及体积。
证明空间线面平行或垂直需注意以下几点:
①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。
④三垂线定理及其逆定理在高考题中使用的频率最高,在证明线线垂直时应优先考虑.应用时常需先认清所观察的平面及它的垂线,从而明确斜线、射影、面内直线的位置,再根据定理由已知的两直线垂直得出新的两直线垂直.另外通过计算证明线线垂直也是常用的方法之一。
垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系:
题型1:线线垂直问题
例1.如图1所示,已知正方体ABCD-A1B1C1D1中,E、F、G、H、L、M、N分别为A1D1,A1B1,BC,CD,DA,DE,CL的中点,求证:EF⊥GF。
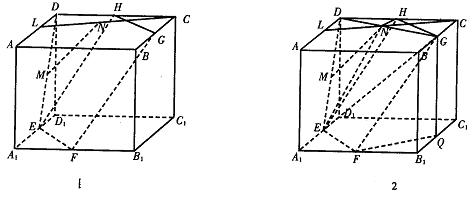

证明:如图2,作GQ⊥B1C1于Q,连接FQ,则GQ⊥平面A1B1C1D1,且Q为B1C1的中点。
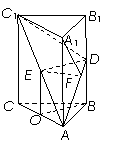 在正方形A1B1C1D1中,由E、F、Q分别为A1D1、A1B1、B1C1的中点可证明EF⊥FQ,由三垂线定理得EF⊥GF。
在正方形A1B1C1D1中,由E、F、Q分别为A1D1、A1B1、B1C1的中点可证明EF⊥FQ,由三垂线定理得EF⊥GF。
点评:以垂直为背景,加强空间想象能力的考查,体现了立体几何从考查、论证思想。
例2.(2006全国Ⅱ,19)如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点,证明:ED为异面直线BB1与AC1的公垂线。
证明:设O为AC中点,连接EO,BO,则EO∥=C1C,又C1C∥=B1B,所以EO∥=DB,EOBD为平行四边形,ED∥OB。
∵AB=BC,∴BO⊥AC,
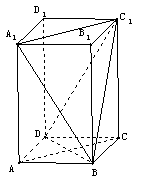 又平面ABC⊥平面ACC1A1,BOÌ面ABC,故BO⊥平面ACC1A1,
又平面ABC⊥平面ACC1A1,BOÌ面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.
点评:该题考点多,具有一定深度,但入手不难,逐渐加深,逻辑推理增强。
题型2:线面垂直问题
例3.(1)(2006北京文,17)如图,ABCD-A1B1C1D1是正四棱柱,求证:BD⊥平面ACC1A1。
(2)(2006天津文,19)如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱 。
。
(I)证明 平面
平面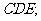 ;
;
(II)设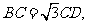 证明
证明 平面。
平面。
证明:(1)∵ABCD-A1B1C1D1是正四棱柱,
∴CC1⊥平面ADCD, 
∴BD⊥CC1
∵ABCD是正方形
∴BD⊥AC
又∵AC,CC1 平面ACC1A1,
平面ACC1A1,
且AC∩CC1=C,
∴BD⊥平面ACC1A1。
(2)证明:
(I)取CD中点M,连结OM。
在矩形ABCD中,  又
又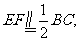

则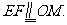 连结EM,于是四边形EFOM为平行四边形。
连结EM,于是四边形EFOM为平行四边形。
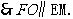

又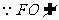 平面CDE,且
平面CDE,且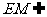 平面CDE,
平面CDE,
 平面CDE。
平面CDE。
(II)连结FM。
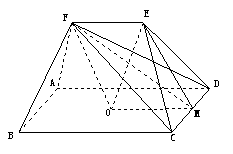 由(I)和已知条件,在等边
由(I)和已知条件,在等边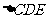 中,
中,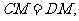
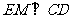

且

因此平行四边形EFOM为菱形,从而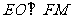 。
。
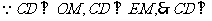 平面EOM,从而
平面EOM,从而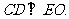

而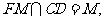 所以
所以 平面
平面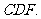

点评:本题考查直线与平面垂直等基础知识,考查空间想象能力和推理论证能力.
 例4.如图,直三棱柱ABC-A1B1C1 中,AC =BC =1,∠ACB =90°,AA1 =
例4.如图,直三棱柱ABC-A1B1C1 中,AC =BC =1,∠ACB =90°,AA1 =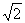 ,D
是A1B1 中点.(1)求证C1D ⊥平面A1B ;(2)当点F
在BB1 上什么位置时,会使得AB1 ⊥平面C1DF ?并证明你的结论。
,D
是A1B1 中点.(1)求证C1D ⊥平面A1B ;(2)当点F
在BB1 上什么位置时,会使得AB1 ⊥平面C1DF ?并证明你的结论。
分析:(1)由于C1D 所在平面A1B1C1 垂直平面A1B ,只要证明C1D 垂直交线A1B1 ,由直线与平面垂直判定定理可得C1D ⊥平面A1B。
(2)由(1)得C1D ⊥AB1 ,只要过D 作AB1 的垂线,它与BB1 的交点即为所求的F
点位置。
(1)证明:如图,∵ ABC-A1B1C1 是直三棱柱,
∴ A1C1 =B1C1 =1,且∠A1C1B1 =90°。
又 D 是A1B1 的中点,∴ C1D ⊥A1B1 。
 ∵ AA1
⊥平面A1B1C1 ,C1D
∵ AA1
⊥平面A1B1C1 ,C1D  平面A1B1C1 ,
平面A1B1C1 ,
∴ AA1 ⊥C1D ,∴ C1D ⊥平面AA1B1B。
(2)解:作DE ⊥AB1 交AB1 于E ,延长DE 交BB1 于F ,连结C1F ,则AB1 ⊥平面C1DF ,点F 即为所求。
事实上,∵ C1D
⊥平面AA1BB ,AB1  平面AA1B1B ,
平面AA1B1B ,
∴ C1D ⊥AB1 .又AB1 ⊥DF ,DF 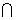 C1D =D ,
C1D =D ,
∴ AB1 ⊥平面C1DF 。
点评:本题(1)的证明中,证得C1D ⊥A1B1 后,由ABC-A1B1C1 是直三棱柱知平面C1A1B1 ⊥平面AA1B1B ,立得C1D ⊥平面AA1B1B。(2)是开放性探索问题,注意采用逆向思维的方法分析问题。
题型3:面面垂直问题
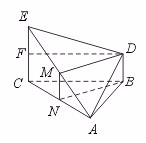 例5.如图,△ABC 为正三角形,EC
⊥平面ABC ,BD ∥CE ,CE =CA =2 BD ,M 是EA 的中点,求证:(1)DE =DA ;(2)平面BDM ⊥平面ECA ;(3)平面DEA ⊥平面ECA。
例5.如图,△ABC 为正三角形,EC
⊥平面ABC ,BD ∥CE ,CE =CA =2 BD ,M 是EA 的中点,求证:(1)DE =DA ;(2)平面BDM ⊥平面ECA ;(3)平面DEA ⊥平面ECA。
分析:(1)证明DE =DA ,可以通过图形分割,证明△DEF ≌△DBA。(2)证明面面垂直的关键在于寻找平面内一直线垂直于另一平面。由(1)知DM
⊥EA ,取AC
中点N ,连结MN
、NB ,易得四边形MNBD 是矩形。从而证明DM
⊥平面ECA。
证明:(1)如图,取EC 中点F
,连结DF。
 ∵ EC ⊥平面ABC ,BD ∥CE ,得DB
⊥平面ABC 。
∵ EC ⊥平面ABC ,BD ∥CE ,得DB
⊥平面ABC 。
∴ DB ⊥AB
,EC ⊥BC。
∵ BD ∥CE
,BD =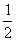 CE =
CE =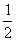 FC ,则四边形FCBD 是矩形,DF
⊥EC。
FC ,则四边形FCBD 是矩形,DF
⊥EC。
又BA =BC =DF ,
∴ Rt△DEF ≌Rt△ABD ,所以DE =DA。
(2)取AC 中点N
,连结MN 、NB ,
∵ M 是EA
的中点,
∴ MN 
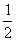 EC。
EC。
 由BD
由BD 
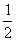 EC ,且BD ⊥平面ABC ,可得四边形MNBD 是矩形,于是DM ⊥MN。
EC ,且BD ⊥平面ABC ,可得四边形MNBD 是矩形,于是DM ⊥MN。
∵ DE =DA
,M 是EA 的中点,
∴ DM ⊥EA
.又EA  MN =M ,
MN =M ,
∴ DM ⊥平面ECA ,而DM  平面BDM ,则平面ECA ⊥平面BDM。
平面BDM ,则平面ECA ⊥平面BDM。
(3)∵ DM ⊥平面ECA ,DM  平面DEA ,
平面DEA ,
∴ 平面DEA ⊥平面ECA。
点评:面面垂直的问题常常转化为线面垂直、线线垂直的问题解决。
例6.(2009江西卷理)(本小题满分12分)
在四棱锥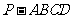 中,底面
中,底面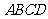 是矩形,
是矩形,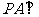 平面
平面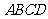 ,
,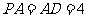 ,
,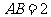 . 以
. 以 的中点
的中点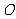 为球心、
为球心、 为直径的球面交
为直径的球面交 于点
于点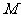 ,交
,交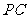 于点
于点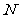 .
.
(1)求证:平面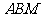 ⊥平面
⊥平面 ;
;
(2)求直线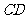 与平面
与平面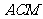 所成的角的大小;
所成的角的大小;
(3)求点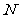 到平面
到平面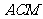 的距离.
的距离.
 解:
解:
方法一:(1)依题设知,AC是所作球面的直径,则AM⊥MC。
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,所以A M⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)由(1)知,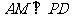 ,又
,又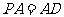 ,则
,则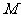 是
是 的中点可得
的中点可得
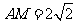 ,
,
则
设D到平面ACM的距离为 ,由
,由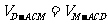 即
即 ,
,
可求得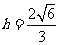 ,
,
设所求角为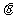 ,则
,则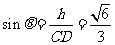 ,
,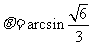 。
。
(1)
可求得PC=6。因为AN⊥NC,由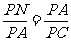 ,得PN
,得PN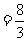 。所以
。所以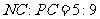 。
。
故N点到平面ACM的距离等于P点到平面ACM距离的 。
。
又因为M是PD的中点,则P、D到平面ACM的距离相等,由(2)可知所求距离为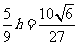 。
。
方法二:
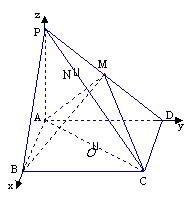 (1)同方法一;
(1)同方法一;
(2)如图所示,建立空间直角坐标系,则 ,
, ,
, ,
, 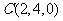 ,
, ,
,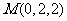 ;设平面
;设平面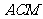 的一个法向量
的一个法向量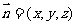 ,由
,由 可得:
可得: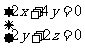 ,令
,令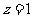 ,则
,则
 。设所求角为
。设所求角为 ,则
,则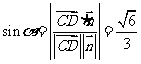 ,
,
所以所求角的大小为 。
。
(3)由条件可得,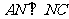 .在
.在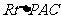 中,
中,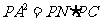 ,所以
,所以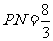 ,则
,则 ,
, 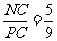 ,所以所求距离等于点
,所以所求距离等于点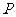 到平面
到平面 距离的
距离的 ,设点
,设点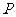 到平面
到平面 距离为
距离为 则
则 ,所以所求距离为
,所以所求距离为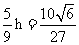 。
。
题型4:射影问题
例7.(1)如图, 正方形
正方形 所在平面,过
所在平面,过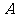 作与
作与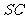 垂直的平面分别交
垂直的平面分别交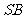 、
、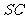 、
、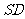 于
于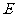 、K、
、K、 ,求证:
,求证: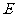 、
、 分别是点
分别是点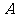 在直线
在直线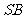 和
和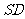 上的射影.
上的射影.
证明:∵  面
面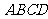 ,∴
,∴ 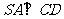 ,
,
∵ 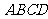 为正方形,∴
为正方形,∴ 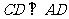 ,
,
∵ 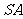 与
与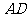 相交,∴
相交,∴  面
面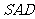 ,
,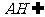 面
面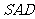 ,
,
∴ 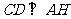 .
.
由已知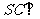 面
面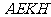 ,且
,且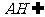 面
面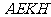 ,
,
∴ 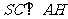 ,
,
 ∵
∵ 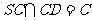 ,∴
,∴ 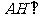 面
面 ,
,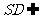 面
面 ,∴
,∴ 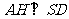 ,
,
即  为点
为点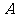 在直线
在直线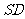 上的射影,
上的射影,
同理可证得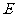 为点
为点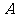 在直线
在直线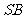 上的射影。
上的射影。
点评:直线与平面垂直的判定定理和性质定理是解决两条直线的主要途径之一,另外,三垂线定理及逆定理、两条直线所成的角等也是证明两条直线垂直的常用的方法.
(2)(2006湖北理,18)如图,在棱长为1的正方体 中,
中,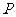 是侧棱
是侧棱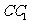 上的一点,
上的一点,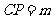 。
。
 (Ⅰ)试确定
(Ⅰ)试确定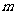 ,使直线
,使直线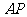 与平面
与平面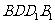 所成角的正切值为
所成角的正切值为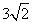 ;
;
(Ⅱ)在线段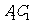 上是否存在一个定点Q,使得对任意的
上是否存在一个定点Q,使得对任意的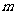 ,D1Q在平面
,D1Q在平面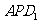 上的射影垂直于
上的射影垂直于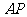 ,并证明你的结论。
,并证明你的结论。
解法1:(Ⅰ)连AC,设AC与BD相交于点O,AP与平面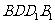 相交于点,连结OG,
相交于点,连结OG,
因为PC∥平面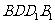 ,平面
,平面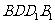 ∩平面APC=OG,
∩平面APC=OG,
故OG∥PC,所以OG=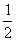 PC=
PC= 。
。
又AO⊥BD,AO⊥BB1,所以AO⊥平面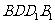 ,
,
故∠AGO是AP与平面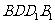 所成的角。
所成的角。
在Rt△AOG中,tanAGO=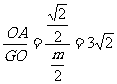 ,即m=
,即m=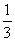 。
。
所以,当m=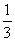 时,直线AP与平面
时,直线AP与平面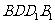 所成的角的正切值为
所成的角的正切值为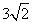 。
。
(Ⅱ)可以推测,点Q应当是AICI的中点O1,
因为D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP 平面ACC1A1,故 D1O1⊥AP。
平面ACC1A1,故 D1O1⊥AP。
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。
点评:本小题主要考查线面关系、直线于平面所成的角的有关知识及空间想象能力和推理运算能力,考查运用向量知识解决数学问题的能力。
例8.如图1所示,已知A1B1C1-ABC是正三棱柱,D是AC的中点。
(1)证明AB1∥DBC1;
(2)假设AB1⊥BC1,BC=2。
求线段AB1在侧面B1BCC1上的射影长.
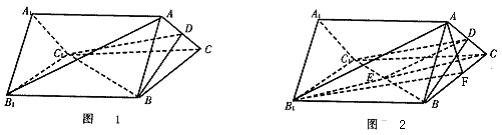
证明:(1)如图2所示,∵A1B1C1-ABC是正三棱柱,
∴四边形B1BCC1是矩形。
连结B1C,交BC1于E,则BE=EC。
连结DE,在△AB1C中,∵AD=DC,
∴DE∥AB1,又因为AB1 平面DBC1,DE
平面DBC1,DE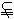 平面DBC1,∴AB1∥平面DBC1。
平面DBC1,∴AB1∥平面DBC1。
(2)作AF⊥BC,垂足为F。因为面ABC⊥面B1BCC1,
∴AF⊥平面B1BCC1。连结B1F,则B1F是AB1在平面B1BCC1内的射影。
∵BC1⊥AB1,∴BC1⊥B1F。
∵四边形B1BCC1是矩形,∴∠B1BF=∠BCC1=90°,又∠FB1B=∠C1BC,∴△B1BF∽△BCC1,则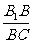 =
=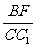 =
=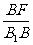 。
。
又F为正三角形ABC的BC边中点,因而B1B2=BF·BC=1×2=2。
于是B1F2=B1B2+BF2=3,∴B1F= ,即线段AB1在平面B1BCC1内的射影长为
,即线段AB1在平面B1BCC1内的射影长为 。
。
点评:建立直线和平面的位置关系与点、线在平面上的射影间的关系。
题型5:垂直的应用
例9.已知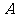 是边长为
是边长为 的正三角形
的正三角形 所在平面外一点,
所在平面外一点,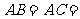
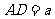 ,求异面直线
,求异面直线 与
与 的距离.
的距离.
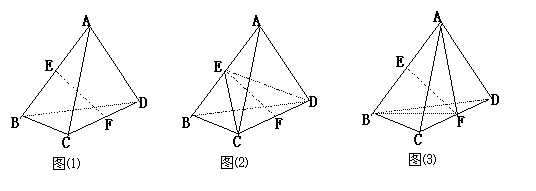
解析:分别取 、
、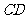 中点
中点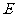 、
、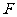 ,连结
,连结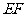 (图⑴)。
(图⑴)。
连结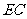 、
、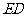 (图⑵)
(图⑵)
∵ ,
, 为公共边,
为公共边, ,
,
∴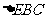 ≌
≌ ∴
∴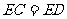
∵点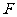 为
为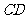 中点 ∴
中点 ∴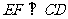 同理:
同理: (图⑶)
(图⑶)
又 ,
,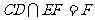 ,
,
∴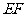 即为异面直线
即为异面直线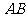 与
与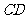 的公垂线段
的公垂线段
如图⑵,在 中,
中,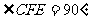 ,
,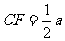 ,
,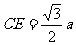 ,
,
 ∴
∴ ∴异面直线
∴异面直线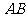 与
与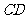 的距离
的距离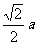 。
。
点评:求异面直线的距离,必须先找到两条异面直线的公垂线段。
例10.如图,在空间四边形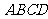 中,
中,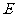 、
、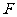 、
、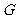 、
、 分别是边
分别是边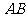 、
、 、
、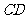 、
、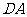 的中点,对角线
的中点,对角线 且它们所成的角为
且它们所成的角为 。
。
⑴求证: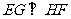 ,⑵求四边形
,⑵求四边形 的面积。
的面积。
解析:⑴在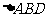 中,
中,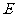 、
、 分别是边
分别是边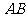 、
、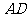 的中点,∴
的中点,∴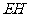 ∥
∥ ,
,
在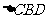 中,
中,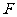 、
、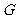 分别是边
分别是边 、
、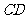 的中点,∴
的中点,∴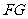 ∥
∥ ,
,
∴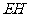 ∥
∥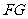 且
且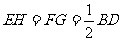 ,
,
同理: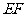 ∥
∥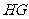 且
且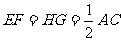 ,
,
∵ ,∴
,∴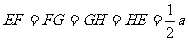 ,
,
∴四边形 为菱形,∴
为菱形,∴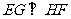 。
。
⑵∵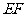 ∥
∥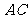 ,
,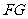 ∥
∥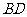 ,
,
∴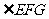 (或
(或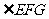 的补角)即为异面直线
的补角)即为异面直线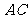 与
与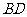 所成的角,
所成的角,
由已知得: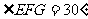 (或
(或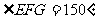 ),
),
∴四边形 的面积为:
的面积为: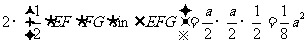 。
。
题型6:课标创新题
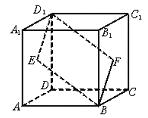
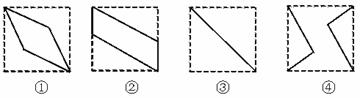
例11.(1)(2000全国,16)如图(1)所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是图(2)的 (要求:把可能的图的序号都填上)
图(1)
图(2)
答案:②③
解析:∵面BFD1E⊥面ADD1A1,所以四边形BFD1E在面ADD1A1上的射影是③,同理,在面BCC1B1上的射影也是③。
过E、F分别作DD1和CC1的垂线,可得四边形BFD1E在面DCC1D1上的射影是②,同理在面ABB1A1,面ABCD和面A1B1C1D1上的射影也是②。
(2)(2000上海,7)命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥.
命题A的等价命题B可以是:底面为正三角形,且 的三棱锥是正三棱锥。
答案:侧棱相等(或侧棱与底面所成角相等……)
解析:要使命题B与命题A等价,则只需保证顶点在底面上的射影S是底面正三角形的外心即可,因此,据射影定理,得侧棱长相等。
例12.(2009宁夏海南卷理)(本小题满分12分)
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
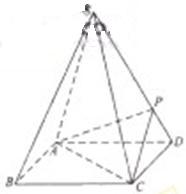
解法一:
(Ⅰ)连BD,设AC交BD于O,由题意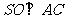 。在正方形ABCD中,
。在正方形ABCD中,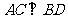 ,所以
,所以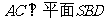 ,得
,得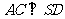 .
.
(Ⅱ)设正方形边长 ,则
,则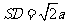 。
。
又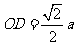 ,所以
,所以 ,
,
连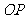 ,由(Ⅰ)知
,由(Ⅰ)知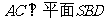 ,所以
,所以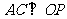 ,
,
且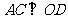 ,所以
,所以 是二面角
是二面角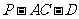 的平面角。
的平面角。
由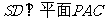 ,知
,知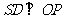 ,所以
,所以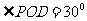 ,
,
即二面角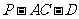 的大小为
的大小为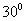 。
。
(Ⅲ)在棱SC上存在一点E,使
由(Ⅱ)可得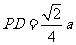 ,故可在
,故可在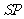 上取一点
上取一点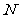 ,使
,使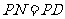 ,过
,过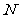 作
作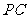 的平行线与
的平行线与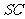 的交点即为
的交点即为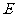 。连BN。在
。连BN。在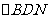 中知
中知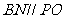 ,又由于
,又由于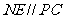 ,故平面
,故平面 ,得
,得 ,由于
,由于 ,故
,故 .
.
解法二:
(Ⅰ);连 ,设
,设 交于
交于 于
于 ,由题意知
,由题意知 .以O为坐标原点,
.以O为坐标原点, 分别为
分别为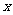 轴、
轴、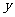 轴、
轴、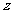 轴正方向,建立坐标系
轴正方向,建立坐标系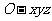 如图.
如图.
设底面边长为 ,则高
,则高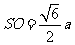 。
。
于是
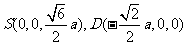
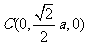



故 
从而 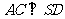
(Ⅱ)由题设知,平面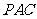 的一个法向量
的一个法向量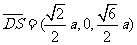 ,平面
,平面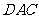 的一个法向量
的一个法向量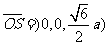 ,设所求二面角为
,设所求二面角为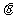 ,则
,则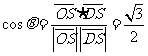 ,所求二面角的大小为
,所求二面角的大小为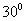
(Ⅲ)在棱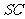 上存在一点
上存在一点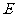 使
使 .
.
由(Ⅱ)知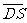 是平面
是平面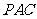 的一个法向量,
的一个法向量,
且 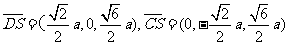
设 
则 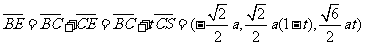
而 
即当 时,
时,
而试题详情
3.面面垂直
两个平面垂直的定义:相交成直二面角的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直 面面垂直)
面面垂直)
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
两平面垂直的性质定理:(面面垂直 线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com