
22.(本题满分12分)
已知函数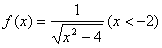 .
.
(Ⅰ) 求f –1(x);
(Ⅱ) 若数列{an}的首项为a1=1, (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;
(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn< 成立. 若存在,求出k的值;若不存在,说明理由.
成立. 若存在,求出k的值;若不存在,说明理由.
豫南九校2009-2010学年上期第一次联考
21.(本题满分12分)
已知函数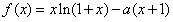 ,其中
,其中 为常数.
为常数.
(Ⅰ)当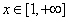 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅱ)求 的单调区间.
的单调区间.
20.(本题满分12分)
已知数列{an}满足
(Ⅰ)求数列的前三项:a1,a2,a3;
(Ⅱ)试确定λ的值,使数列 为等差数列;
为等差数列;
(Ⅲ)求数列{an}的前n项和Sn.
17.(本题满分10分)
已知函数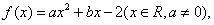
(Ⅰ)判断函数 的奇偶性;
的奇偶性;
(Ⅱ) 时,方程
时,方程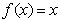 的两实根
的两实根 满足
满足 ,求证:
,求证: .
.
18 (本题满分12分)
已知集合A= ,
, .
.
(Ⅰ) 当a=2时,求A B;
B;
(Ⅱ) 求使B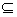 A的实数a的取值范围.
A的实数a的取值范围.
19 (本题满分12分)
为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

13
设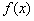 、
、 分别是定义在R上的奇函数和偶函数,当x<0时
分别是定义在R上的奇函数和偶函数,当x<0时
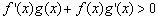 且
且 ,则不等式
,则不等式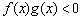 的解集为
;
的解集为
;
14 定义集合运算:A⊙B={z│z=xy(x+y),x∈A,y∈B}.设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为 ;
15
设函数f(x)=
 在x=0处连续,则a=
在x=0处连续,则a=
16
数列 中,如果存在非零常数
中,如果存在非零常数 ,使得
,使得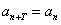 对于任意的非零自然数
对于任意的非零自然数 均成 立,那么就称数列
均成 立,那么就称数列 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列 的周期。已知数列
的周期。已知数列 满足
满足
 ,如果
,如果 ,当数列
,当数列 的周期最小时,求该数列前2009项和是
____________.
的周期最小时,求该数列前2009项和是
____________.
12.
已知函数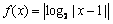 ,且关于x的方程
,且关于x的方程 有6个不同的实数解,若最小实数解为
– 3,则a + b的值为
有6个不同的实数解,若最小实数解为
– 3,则a + b的值为
A.– 3 B.– 2 C.0 D.不能确定
第Ⅱ卷
11. .函数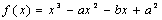 ,当x=1时,有极值10,则a,b的值为
,当x=1时,有极值10,则a,b的值为
A .a=3,b=-3或a=-4,b=11 B.a=-4,b=11 C .a=-1,b=5 D . a=3,b=-3
10.设数列 满足
满足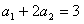 ,且对任意的
,且对任意的 ,点
,点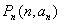 都有
都有 ,则
,则 的前
的前 项和
项和 为
为
A. B.
B. C.
C.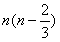 D.
D.
9. 函数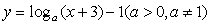 的图象恒过点A,若点A在直线
的图象恒过点A,若点A在直线
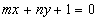 上,其中m
上,其中m 的最小值为
的最小值为
A. 10 B. 9 C. 8 D. 7
8.
等差数列 的公差
的公差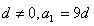 ,若
,若 与
与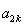 的等比中项,则
的等比中项,则
A.2 B.4 C.6 D.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com