
2.过程与方法:通过学生感兴趣的上网问题引入一元二次不等式的有关概念,通过让学生比较两种不同的收费方式,抽象出不等关系;利用计算机将数学知识用程序表示出来;
1.知识与技能:从实际问题中建立一元二次不等式,解一元二次不等式;能把一元二次不等式的解的类型归纳出来;
2.一元二次不等式恒成立的问题
1.从不等式的解集出发求不等式中参数的值或范围的问题;
(二)典例分析
例1.解不等式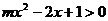

例2.已知关于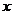 的不等式
的不等式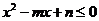 的解集是
的解集是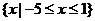 ,求实数
,求实数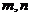 之值.
之值.
例3.已知不等式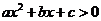 的解集为
的解集为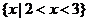 求不等式
求不等式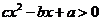 的解集.
的解集.
解:由题意 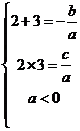 , 即
, 即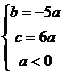 .代入不等式
.代入不等式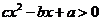 得:
得:
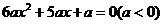 .即
.即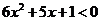 ,
,
 所求不等式的解集为
所求不等式的解集为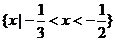 .
.
例4.已知一元二次不等式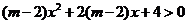 的解集为
的解集为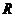 ,求
,求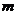 的取值范围.
的取值范围.
解: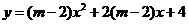 为二次函数,
为二次函数,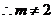
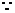 二次函数的值恒大于零,即
二次函数的值恒大于零,即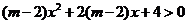 的解集为
的解集为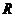 .
.
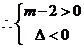 , 即
, 即 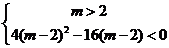 ,解得:
,解得: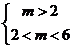
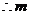 的取值范围为
的取值范围为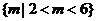
变式:
1.已知二次函数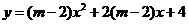 的值恒大于零,求
的值恒大于零,求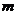 的取值范围.
的取值范围.
2.已知一元二次不等式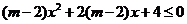 的解集为
的解集为 ,求
,求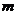 的取值范围.
的取值范围.
例5.若函数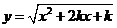 中自变量
中自变量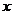 的取值范围是一切实数,求
的取值范围是一切实数,求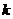 的取值范围
的取值范围
解: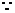
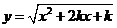 中自变量
中自变量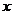 的取值范围是
的取值范围是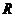 ,
, 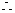
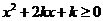 恒成立.
恒成立.
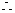
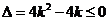
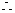
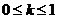
故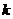 的取值范围是
的取值范围是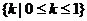 .
.
思考题:若不等式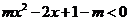 对满足
对满足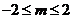 的所有
的所有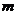 都成立,求实数
都成立,求实数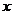 的取值范围.
的取值范围.
解:已知不等式可化为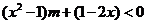 .
.
设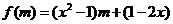 ,这是一个关于
,这是一个关于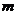 的一次函数(或常数函数),从图象上看,
的一次函数(或常数函数),从图象上看,
要使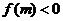 在
在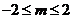 时恒成立,其等价条件是:
时恒成立,其等价条件是:
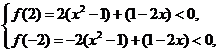 即
即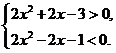 解得
解得 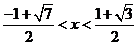 .
.
所以,实数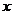 的取值范围是
的取值范围是 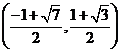 .
.
(一)复习引入
1、 列表复习一元二次函数的图象、一元二次方程的根、一元二次不等式的解集的关系:
2、由上表引导学生观察出: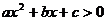 对一切
对一切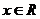 都成立的条件为:
都成立的条件为: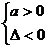

 对一切
对一切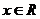 都成立的条件为:
都成立的条件为:

从不等式的解集出发求不等式中参数的值或范围的问题,掌握一元二次不等式恒成立的解题思路.
(1)掌握利用二次函数图象求解一元二次不等式的方法;
(2)从不等式的解集出发求不等式中参数的值或范围的问题;
(3)从二次函数或是一元二次方程的角度,来解决一元二次不等式的综合题. 
1.某公司招收男职员x名,女职员y名,x和y须满足约束条件:
则z=10x+10y的最大值是:( )
A. 80 B. 85 C. 90 D.95
4、课堂小结:
解线性规划应用题的一般步骤:
(1)设出所求的未知数;
(2)列出约束条件;
(3)建立目标函数;
(4)作出可行域;
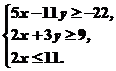 (5)运用平移法求出最优解。
(5)运用平移法求出最优解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com