
6.已知点P(x,y)的坐标满足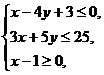 设A(2,0),则
设A(2,0),则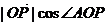 (O为坐标原点)的最大值为___________.
(O为坐标原点)的最大值为___________.
答案:5
解析: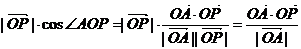 ,
,
∵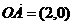 ,
,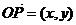 ,
,
∴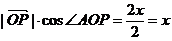 .
.
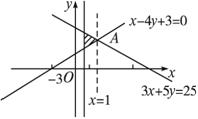
画出可行域,易知点A的横坐标即为所求.
5.设函数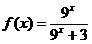 ,计算和
,计算和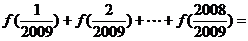 __________.
__________.
答案:1004
解析:由于
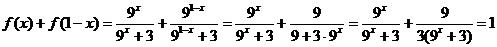 .
.
设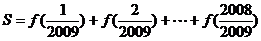 ,
,
又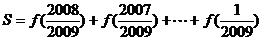 ,
,
∴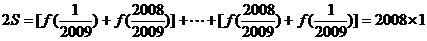 .
.
∴S=1004.
4.若f(n)表示n2+1(n∈N*)的各位数字之和,如:62=36,36+1=37,3+7=10,则f(6)=10,记f1(n)= f(n),f2(n)=f(f1(n)),…fk+1 (n)=f(fk(n))(k∈N*),则f2009 (8)=_________.
答案:5
解析:本题考查归纳猜想的能力及数列的周期性.82=64,64+1=65,6+5=11,∴f1(8)=f(8)=11;
112=121,121+1=122,1+2+2=5,∴f2(8)=5;
52=25,25+1=26,2+6=8,∴f3(8)=8;
82=64,64+1=65,6+5=11,∴f4(8)=11.
由此猜想fk(8)是一个周期为3的数列,所以f2009 (8)=f3×669+2 (8)=f2(8)=5.
3.已知数列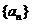 的前n项和为
的前n项和为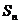 ,对任意n∈N*,都有
,对任意n∈N*,都有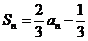 ,且
,且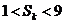 (k∈N*),则
(k∈N*),则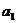 的值为__________,k的值为__________.
的值为__________,k的值为__________.
答案:-1 14
解析:当n=1时,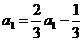 ,可知(a1=-l,当n ≥ 2时,
,可知(a1=-l,当n ≥ 2时,
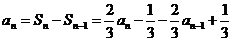 ,可知
,可知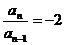 ,即{an}是等比数列,得
,即{an}是等比数列,得
an=-1(-2)n-1,得a1=-1,a2=2,a3=-4,a4=8,a5=-16,因为S3<0,S4=5,S5=-8,S6=20,所以当k=4时符合题意.本题主要考查数列的通项公式的求解问题,知道an与Sn的关系式求数列的通项公式问题是一类热点问题,经常考查,在复习时要加强这类题的学习与总结.
答案:D.
2.(宣武·理·题13)
若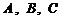 为
为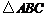 的三个内角,则
的三个内角,则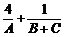 的最小值为
.
的最小值为
.
解析: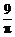 ;
;
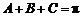 ,且
,且
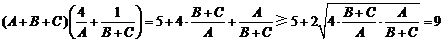 ,
,
因此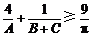 ,当且仅当
,当且仅当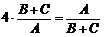 ,即
,即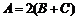 时等号成立.
时等号成立.
1.(宣武·文·题13)设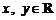 ,且满足
,且满足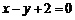 ,则
,则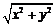 的最小值为 ;若
的最小值为 ;若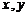 又满足
又满足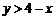 ,则
,则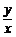 的取值范围是
.
的取值范围是
.
解析: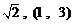 ;
;
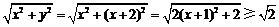 ,当
,当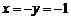 时取等号;
时取等号;
画出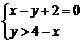 的可行域,为射线
的可行域,为射线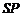 (如图),要求的就是
(如图),要求的就是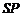 上的点与原点连线的斜率,易算出
上的点与原点连线的斜率,易算出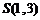 ,斜率的范围为
,斜率的范围为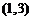 .
.
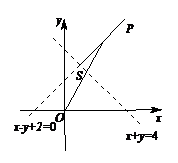
4.数列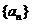 满足:
满足: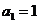 ,且对任意的
,且对任意的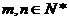 都有:
都有: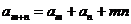 ,则
,则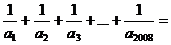 ( )
( )
A.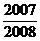 B.
B.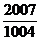 C.
C.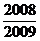 D.
D.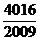
答案:D
解析:因为∵an+m=an+am+m n,则可得al=l,a2=3,a3=6,a4=10,…,则可猜得数列的通项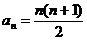 ,·∴
,·∴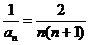 =
=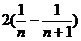 ,
,
∴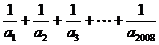 =
=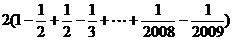
=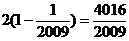 ,
,
故选择D.本题考查了求解数列的通项的方法和数列求和的方法.求解数列的通项除了依据数列的递推关系,恰当应用方法求解通项外,还可以通过有限项归纳出数列的项的共同特点,而猜出通项.
3.(丰台·理·题7)
设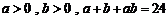 ,则( )
,则( )
A.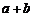 有最大值
有最大值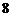 B.
B.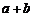 有最小值
有最小值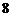
C. 有最大值
有最大值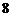 D.
D. 有最小值
有最小值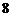
[解析] B;
∵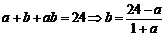
∴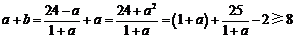 ;
;
而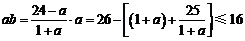 .
.
2.已知等比数列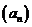 中
中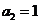 ,则其前3项的和
,则其前3项的和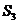 的取值范围是( )
的取值范围是( )
A.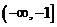 B.
B. C.
C.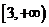 D.
D.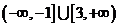
解析:设公比为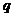 ,
,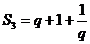 ,由
,由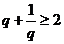 或
或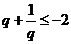 ,所以取值范围为
,所以取值范围为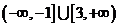 .
.
1.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次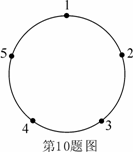 沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从
沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从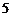 这点开始跳,则经2009次跳后它停在的点所对应的数为( )
这点开始跳,则经2009次跳后它停在的点所对应的数为( )
A.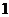 B.
B.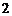 C.
C.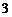 D.
D.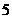
解析:5-2-1-3-5,周期为4,2009=4×502+1,经过2009次跳后它停在的点所对应的数为2.
答案:B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com