2. 求数列前n项和　　

1. 求数列前n项和

(当n为奇数时，；当n为偶数时，)

特殊数列求和、拆项法、裂项法、错位法

例7 求数列前n项和

　解：　　　　 ①

　②

两式相减：

例5求数列前n项和

解：设数列的通项为b_n，则

例6求数列前n项和

　 解：

例4求数列

的前n项和

　 解：设数列的通项为a_n，前n项和为S_n，

则

当时，

当时，

例1 设等差数列{a_n}的前n项和为S_n，且，

求数列{a_n}的前n项和

　 解：取n =1，则

又： 　可得：

例2 大楼共n层，现每层指定一人，共n人集中到设在第k层的临时会议室开会，问k如何确定能使n位参加人员上、下楼梯所走的路程总和最短(假定相邻两层楼梯长相等)

解：设相邻两层楼梯长为a，则

当n为奇数时，取　 S达到最小值

当n为偶数时，取　 S达到最大值　

例3 求和S=1×2×3+2×3×4+…+n(n+1)(n+2)．

例　 因为n(n+1)(n+2)=n+3n+2n，则

S_n=1+3×1+2×1+2+3×2+2×2+…n+3n+2n

=(1+2…+n)+3(1+2+…+n)+2(1+2+…+n)

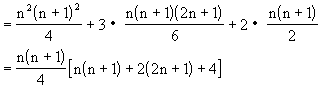
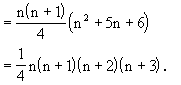
以上应用了特殊公式和分组求解的方法

2．等比数列的前n项和公式：

　 当时， ①　 或　 ②

当q=1时，

1.等差数列的前项和公式：

，

29．(本题共18分)

　　　 A、B、C、D、E、F分别是KCl 、Mg(NO₃)₂、Ba(OH)₂、AgNO₃、Na₂CO₃、(NH₄)₂SO₄六种溶液的一种，将它们两两混合后，现象如下表。表中用“↑”代表产生气体，用“↓”代表产生沉淀，用“-”代表无现象。

　　　 试回答下列问题：

　 (1)这六种溶液分别是(填化学式)A　　　　　　 　B　　　　　　 　C　　　　　　

D　　　　　　　 　E　　　　　　　　 　F　　　　　　　　

　 (2)试写出A与B反应的离子方程式：　　　　　　　　　　　　　　　　　　　

　 (3)向E中逐滴加入氨水的现象是 　　　　　　　　　　　　　　　　　　　离子方程式为