6．若P(2，－1)为圆(θ为参数且0≤θ<2π)的弦的中点，则该弦所在的直线方程为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．x+y+3＝0　 　　　　　B．x+y－3＝0

C．x－y－3＝0　 　　　　　D．x－y+3＝0

解析：∵圆

消去θ，得(x－1)²+y²＝25，

∴圆心C(1,0)，∴k_CP＝－1.

∴弦所在的直线的斜率为1.

∴弦所在的直线方程为y－(－1)＝1·(x－2)，

即为x－y－3＝0.

答案：C

5．点P(x，y)是椭圆2x²+3y²＝12上的一个动点，则x+2y的最大值为　　　　　　　 (　)

A.　 　　　　　B.　　　　　　 C.　 　　　　　　D．2

解析：椭圆+＝1，设点P(cosθ，2sinθ)，

则x+2y＝cosθ+4sinθ＝sin(θ+φ)≤.

答案：B

4．设直线参数方程为(t为参数)，则它的斜截式方程为　　　　　　　 (　)

　A．y＝x+(2－3)　 　　　　　B．y＝x+(3－2)

C．y＝x+(2－3)　 　　　　　D．y＝x+(3－2)

解析：设直线的斜率为，当t＝－4时，x＝0，y＝3－2，故直线的斜截式方程为y＝

x+( 3－2)．

答案：B

3．已知点P(x，y)在曲线(θ为参数)上，则的取值范围为　　　　　 (　)

A．(－，]　 　　　　B．[－，]　　　　 C．[－1,1]　 　　　D．[－，]

解析：　曲线(θ为参数)是以(－2,0)为圆心，以1为半径的圆，设＝k，求的取值范围，即求当直线y＝kx与圆有公共点时k的取值范围，如图结合圆的几何性质可得－≤k≤.

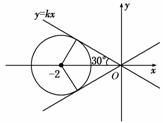
答案：B

2．(2009·广东高考)若直线(t为参数)与直线4x+ky＝1垂直，则常数k＝(　)

A．25 　　　　B．－6　　　　　　　　　 C．6　 　　　D．7

解析：直线l₁：3x+2y－7＝0，直线l₂：4x+ky－1＝0.

由l₁⊥l₂，∴2k+3·4＝0，∴k＝－6.

答案：B

1．(2009·天津高考)设直线l₁的参数方程为(t为参数)，直线l₂的方程为y＝3x+4，则l₁与l₂间的距离为　　　 　　　　　　　　　　　　　　　　　　　　　　　　(　)

A.　　　　B.　　　　　　 C.　 　　　　　　D．3

解析：直线l₁的参数方程(t为参数)．

化为普通方程为：＝，即 3x－y－2＝0.

又l₂：3x－y+4＝0.由两平行线间距离公式知

d＝＝＝.

答案：B　

12．设f(x)＝x²+ax+b，求证：|f(1)|，|f(2)|，|f(3)|中至少有一个不小于.

证明：假设|f(1)|＜，|f(2)|＜，|f(3)|＜，则有

于是有

由①②得－4＜a＜－2；由②③得－6＜a＜－4.两式互相矛盾，所以假设不成立．所以原命题成立，即|f(1)|，|f(2)|，|f(3)|中至少有一个不小于.

11．△ABC的三个内角A、B、C成等差数列，a、b、c分别为三内角A，B，C的对边．求证：+＝.

证明：要证明+＝，

只需证明+＝3，

只需证明+＝1，

只需证明c(b+c)+a(a+b)＝(a+b)·(b+c)，

只需证明c²+a²＝ac+b²，

∵△ABC的三个内角A，B，C成等差数列，∴B＝60°，

由余弦定理，有b²＝c²+a²－2accos60°，

即b²＝c²+a²－ac，

∴c²+a²＝ac+b².故原命题成立，得证．

10．设a，b，c，d都是小于1的正数，求证：4a(1－b),4b(1－c),4c(1－d),4d(1－a)这四个数不可能都大于1.

证明：假设4a(1－b)＞1,4b(1－c)＞1,4c(1－d)＞1，4d(1－a)＞1，则有

a(1－b)＞，b(1－c)＞，

c(1－d)＞，d(1－a)＞.

∴＞，＞，

＞，＞.

又∵≤，

≤，

≤，≤，

∴＞，＞，

＞，＞.

将上面各式相加得2＞2，矛盾．

∴4a(1－b),4b(1－c),4c(1－d),4d(1－a)这四个数不可能都大于1.

9．求证：a³+b³+c³≥(a²+b²+c²)(a+b+c)．

证明：∵a²+b²≥2ab，∴(a²+b²)(a+b)≥2ab(a+b)，

∴a³+b³+a²b+ab²≥2a²b+2ab²，

∴a³+b³≥a²b+ab².

同理：b³+c³≥b²c+bc²，a³+c³≥a²c+ac².

将三式相加得：

2(a³+b³+c³)≥a²b+ab²+b²c+bc²+a²c+ac².

∴3(a³+b³+c³)≥(a³+a²b+a²c)+(b³+b²a+b²c)+(c³+c²a+c²b)＝(a+b+c)(a²+b²+c²)，

∴a³+b³+c³≥(a²+b²+c²)(a+b+c)．