
1.通过电能转变为化学能的探究活动,了解电解池工作原理,能正确书写电解池的阴、阳极的电极反应式及电解反应方程式。
思考题:1 已知
已知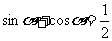 ,求下列各式的值
,求下列各式的值
①sin3α+cos3α ②sin4α+cos4α ③sin6α+cos6α
分析:由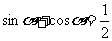 两边平方,整理得
两边平方,整理得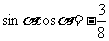
然后将各式化成关于sinα+cosα,sinαcosα的式子将上两式的值代入即可求得各式的值 答案:①
答案:①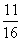 ②
② ③
③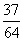
注意:sinα+cosα、sinα·cosα称为关于角α的正弦和余弦的基本对称式,关于sinα、cosα的所有对称式都可以用基本对称式来表示
2 已知sinα·cosα=
已知sinα·cosα=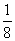 ,且
,且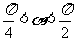 ,则cosα-sinα的值是多少?
,则cosα-sinα的值是多少?
分析:由sinα·cosα=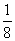 得2sinαcosα=
得2sinαcosα=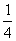
sin2α-2sinαcosα+cos2α=1-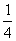
(cosα-sinα)2=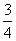
∵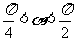 ,∴cosα<sinα,
,∴cosα<sinα,
即cosα-sinα<0
∴cosα-sinα=-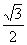

已知角的一个三角函数值求其他三角函数值时,应用平方关系确定符号是个难点,一般地说,这类计算题可分为以下三种情况:⑴已知象限,由象限定符号;⑵已知值,由值分情况讨论;⑶值是字母,开平方时,分情况讨论
3.已知tan =-3,则sin
=-3,则sin = ,cot
= ,cot = .
= .
思路分析:由tan =-3<0知,
=-3<0知, 在第二或第四象限,
在第二或第四象限,
∴可分类后用同角三角函数基本关系求解.(略)
由于这是一个填空题,
∴可先将角 视为锐角,求出sin
视为锐角,求出sin 和cot
和cot 的值,然后具体的再看
的值,然后具体的再看 角所在象限得出sin
角所在象限得出sin 、cot
、cot 的符号.
的符号.
将 视为锐角
视为锐角 ′,则有tan
′,则有tan ′=3,
′=3,
∴ ′=
′=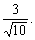 cot
cot ′=
′=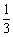 ,
,
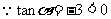 ∴
∴ 在第Ⅱ或第Ⅳ象限.
在第Ⅱ或第Ⅳ象限.
∴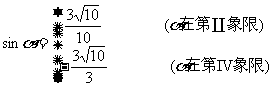
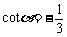

2.已知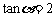 ,求
,求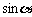 的值
的值
解∵ tan  = 2 > 0,∴
= 2 > 0,∴ 在Ⅰ、Ⅲ象限
在Ⅰ、Ⅲ象限
①当 在Ⅰ象限时.
在Ⅰ象限时.
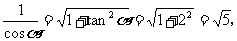
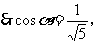
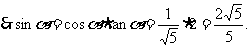
②当 在Ⅲ象限时
在Ⅲ象限时
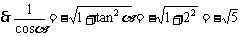 ,
,

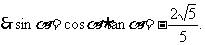
注意:此题在求出cos 的值以后,若直接用平方关系求sin
的值以后,若直接用平方关系求sin 的值,有符号判断问题,需要再分类,就出现二次分类增添了解决问题的复杂性.本题采用了商数关系,避开了引用平方关系求sin
的值,有符号判断问题,需要再分类,就出现二次分类增添了解决问题的复杂性.本题采用了商数关系,避开了引用平方关系求sin 值,使得问题轻松获解.
值,使得问题轻松获解.
1.已知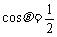 , 求
, 求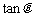 的值.
的值.
解法1: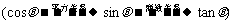
∵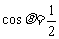 , ∴
, ∴ 在Ⅰ、Ⅳ象限,
在Ⅰ、Ⅳ象限,
当α在Ⅰ象限时,
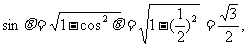
∴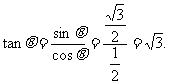
当 在Ⅳ象限时
在Ⅳ象限时
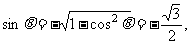
∴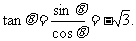
解法2: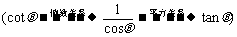
当 在Ⅰ象限时,
在Ⅰ象限时,
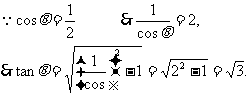
当 在Ⅳ象限时
在Ⅳ象限时
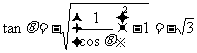
例1. 已知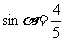 ,并且
,并且 是第二象限角,求
是第二象限角,求 的其他三角函数值.
的其他三角函数值.
分析:由平方关系可求cos 的值,由已知条件和cos
的值,由已知条件和cos 的值可以求tan
的值可以求tan 的值,进而用倒数关系求得cot
的值,进而用倒数关系求得cot 的值.
的值.
解:∵sin2α+cos2α=1, 是第二象限角
是第二象限角
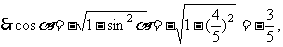
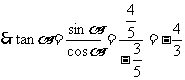
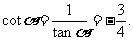
例2.已知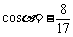 ,求sin
,求sin 、tan
、tan 的值.
的值.
分析:∵cosα<0 ∴ 是第二或第三象限角.因此要对
是第二或第三象限角.因此要对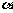 所在象限分类.
所在象限分类.
当 是第二象限角时,
是第二象限角时,
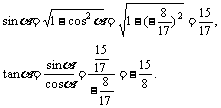
当 是第三象限时
是第三象限时
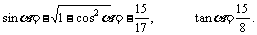
提问:不计算sin 的值,能否算得tan
的值,能否算得tan 的值?
的值?
由于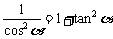 而
而 在Ⅱ或III象限
在Ⅱ或III象限
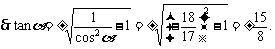
例3.已知tan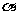 为非零实数,用tan
为非零实数,用tan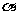 表示sin
表示sin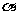 ,cos
,cos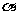 .
.
解:由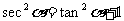 即
即 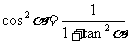
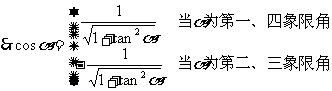
而 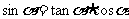
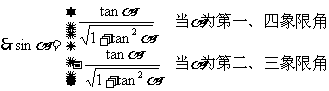
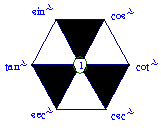
6.这些关系式还可以如图样加强形象记忆:
①对角线上两个函数的乘积为1(倒数关系)
②任一角的函数等于与其相邻的两个函数的积(商数关系)
③阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)
4.点题:三种关系,八个公式,称为同角三角函数的基本关系
 5.注意:
5.注意:
1°“同角”的概念与角的表达形式无关,
如: 
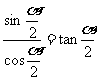
2°上述关系(公式)都必须在定义域允许的范围内成立
3°据此,由一个角的任一三角函数值可求出这个角的其余各三角函数值,且因为利用“平方关系”公式,最终需求平方根,会出现两解,因此应尽可能少用,若使用时,要注意讨论符号
3.推广: 这种关系称为平方关系,类似的平方关系还有:
这种关系称为平方关系,类似的平方关系还有:

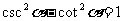
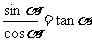 这种关系称为商数关系,类似的商数关系还有:
这种关系称为商数关系,类似的商数关系还有: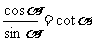
 这种关系称为倒数关系
这种关系称为倒数关系 类似的倒数关系还有:
类似的倒数关系还有: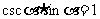
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com