
1(一中2008-2009月考理18).已知数列{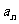 }中,
}中,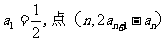 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(1)令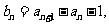 求证数列
求证数列 是等比数列;
是等比数列;
(2)求数列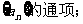
⑶ 设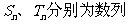
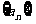
 的前n项和,是否存在实数
的前n项和,是否存在实数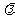 ,使得数列
,使得数列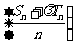 为等差数列?若存在,试求出
为等差数列?若存在,试求出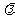 .若不存在,则说明理由。
.若不存在,则说明理由。
解:(I)由已知得 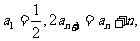
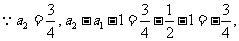
又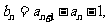
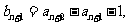
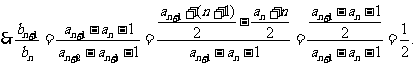
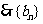 是以
是以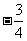 为首项,以
为首项,以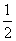 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,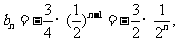
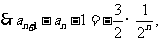
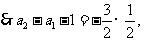



将以上各式相加得:
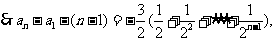
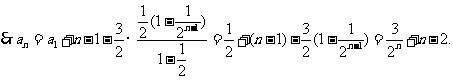
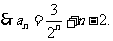
(III)解法一:
存在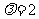 ,使数列
,使数列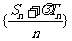 是等差数列.
是等差数列.
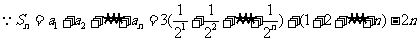

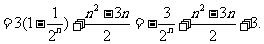
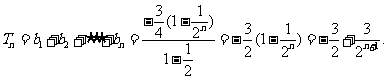
数列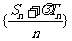 是等差数列的充要条件是
是等差数列的充要条件是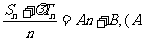 、
、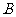 是常数
是常数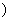
即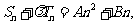
又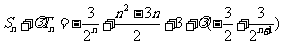

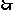 当且仅当
当且仅当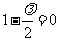 ,即
,即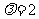 时,数列
时,数列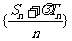 为等差数列.
为等差数列.
解法二:
存在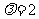 ,使数列
,使数列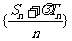 是等差数列.
是等差数列.
由(I)、(II)知,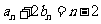
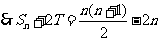
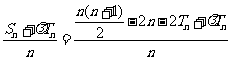
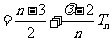
又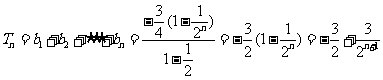

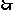 当且仅当
当且仅当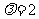 时,数列
时,数列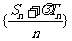 是等差数列.
是等差数列.
2(2009年滨海新区五所重点学校联考理22).(本小题满分14分)
已知等比数列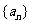 的各项均为正数,且公比不等于1,数列
的各项均为正数,且公比不等于1,数列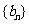 对任意正整数n,均有:
对任意正整数n,均有: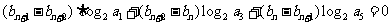
成立,又 。
。
(Ⅰ)求数列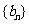 的通项公式及前n项和
的通项公式及前n项和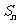 ;
;
(Ⅱ)在数列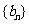 中依次取出第1项,第2项,第4项,第8项,……,第
中依次取出第1项,第2项,第4项,第8项,……,第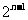 项,……,组成一个新数列
项,……,组成一个新数列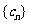 ,求数列
,求数列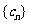 的前n项和
的前n项和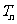 ;
;
(Ⅲ)当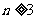 时,比较
时,比较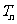 与
与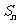 的大小。
的大小。
22.(本小题满分14分)
解:(I)设公比为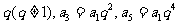 ……………………2分
……………………2分
代入
得
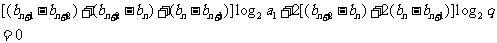
即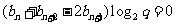
∵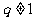 ,∴
,∴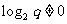 ,∴
,∴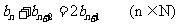
∴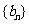 是等差数列 ……………………4分
是等差数列 ……………………4分
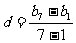 =2 ∴
=2 ∴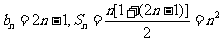 …………6分
…………6分
(Ⅱ)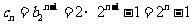
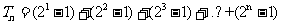
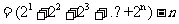
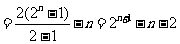 ……………………8分
……………………8分
(3)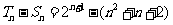
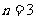 时,
时,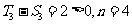 时,
时,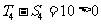
猜测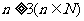 时,
时,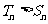 ……………………10分
……………………10分
用数学归纳法证明如下
(1)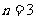 时,
时,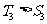 (已证)
(已证)
(2)假设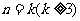 时不等式成立,即
时不等式成立,即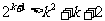 ……………………12分
……………………12分
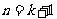 时,
时,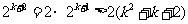
又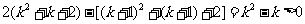
∴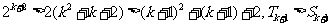
即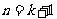 时,不等式成立。
时,不等式成立。
由(1)(2)知,当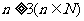 时,
时,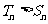 ……………14分
……………14分
3(2009年滨海新区五所重点学校联考文21).(本小题满分14分)
已知数列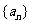 的前
的前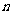 项和
项和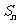 和通项
和通项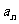 满足
满足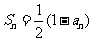 .
.
(Ⅰ)求数列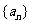 的通项公式;
的通项公式;
(Ⅱ)
求证: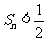 ;
;
(Ⅲ)设函数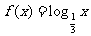 ,
,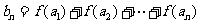 ,
,
求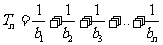 .
.
1(2009年滨海新区五所重点学校联考文12). 等差数列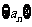 各项都是正数,且
各项都是正数,且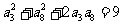 ,则它的前10项和
,则它的前10项和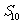 等于 12. 15
等于 12. 15
2(汉沽一中2009届月考文11).已知等差数列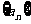 的公差为2,若
的公差为2,若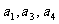 成等比数列, 则
成等比数列, 则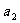 =___________ 11 -4
=___________ 11 -4
3(武清区2008~2009学年度期中理)若数列{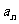 }的前
}的前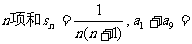
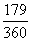
4(武清区2008~2009学年度期中理)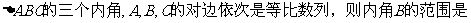
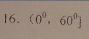
5(和平区2008年高考数学(文)三模13). 已知各项均正的等比数列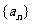 中,
中,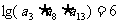 ,则
,则 的值为 。
的值为 。
13. 10000
6(和平区2008年高考数学(理)三模15). 已知数列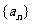 的通项公式
的通项公式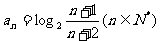 ,设数列
,设数列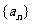 的前n项的和为
的前n项的和为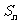 ,则使
,则使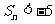 成立的正整数n的最小值为 。63
成立的正整数n的最小值为 。63
7(一中2008-2009月考理14).已知等差数列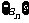 ,若
,若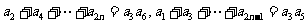 ,且
,且 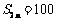 ,则公差=__ _。2
,则公差=__ _。2
1(汉沽一中2008~2009届月考理5).已知等差数列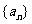 的公差
的公差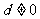 ,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是(B)
,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是(B)
A.4 B.3 C.2 D.
2 (汉沽一中2008~2009届月考文7)、已知
(汉沽一中2008~2009届月考文7)、已知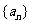 是等差数列,
是等差数列,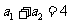 ,
,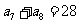 ,则该数列前10项和
,则该数列前10项和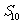 等于( )
等于( )
A.64 B.100 C.110 D.120
[答案]B
[命题意图]本题主要考查等差数列的通项公式、求和公式以及考查学生的运算能力和方程的思想方法.
[解析]设公差为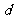 ,
,
则由已知得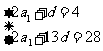
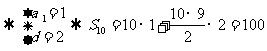
3(汉沽一中2009届月考文7).四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2009次互换座位后,小兔的座位对应的是 ( A )
|
1 鼠 |
2 猴 |
|
1 兔 |
2 猫 |
|
1 猫 |
2 兔 |
|
1 猴 |
2 鼠 |
||||||
|
兔 3 |
猫 4 |
|
鼠 3 |
猴 4 |
|
猴 3 |
鼠 4 |
|
猫 3 |
兔 4 |
||||||
|
开始 |
|
第一次 |
|
第二次 |
|
第三次 |
||||||||||
A.编号1 B. 编号2 C. 编号3 D. 编号4
4(武清区2008~2009学年度期中理)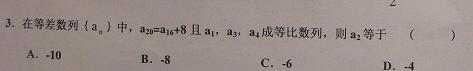
C
5(和平区2008年高考数学(理)三模7). 已知等差数列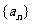 的前n项和为
的前n项和为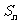 ,若M、N、P三点共线,O为坐标原点,且
,若M、N、P三点共线,O为坐标原点,且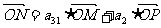 (直线MP不过点O),则
(直线MP不过点O),则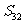 等于(D )
等于(D )
A. 31 B. 32 C. 15 D. 16
6(2009年滨海新区五所重点学校联考理6).已知等比数列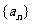 的各项均为正数,公比
的各项均为正数,公比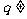 1,设
1,设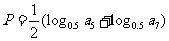 ,
,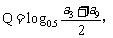 P与Q的大小关系是
( 6.D )
P与Q的大小关系是
( 6.D )
A.P≥Q B.P<Q C.P≤Q D.P>Q
7(2009年滨海新区五所重点学校联考理9).数列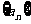 中
中 ;数列
;数列 中,
中,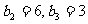 ,
,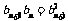 ,在直角坐标平面内,已知点列
,在直角坐标平面内,已知点列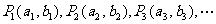
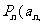 ,
,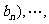 则向量
则向量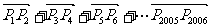 的坐标为 (9.C )
的坐标为 (9.C )
A.(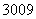 ,8
,8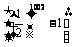 )
B. (
)
B. (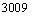 ,8
,8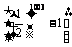 )
)
C. (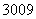 ,8
,8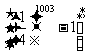 )
D. (
)
D. (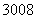 ,8
,8
8(汉沽一中2008~2008学年月考理5).等差数列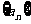 中,
中,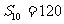 ,那么
,那么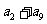 的值是B
的值是B
A. 12 B. 24 C .16 D. 48
1(2009年滨海新区五所重点学校联考理11).二项式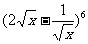 展开式中含x2项的系数是 。 -192
展开式中含x2项的系数是 。 -192
2(汉沽一中2008~2008学年月考理9).由数字0、1、2、3、4组成无重复数字的5位数,其
中奇数有 个。 36
3(汉沽一中2008~2008学年月考理10).二项式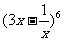 的展开式的常数项是__________. –540
的展开式的常数项是__________. –540
 .
.
1(和平区2008年高考数学(理)三模3). 若二项式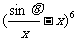 展开式的常数项为20,则
展开式的常数项为20,则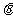 值为(B )
值为(B )
A. 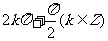 B.
B.
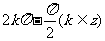
C. 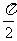 D.
D.
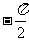
2 (2009年滨海新区五所重点学校联考理10).某电影院第一排共有9个座位,现有3名观众前来就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的做法种数共有 (B )
(2009年滨海新区五所重点学校联考理10).某电影院第一排共有9个座位,现有3名观众前来就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的做法种数共有 (B )
A.18种 B.36种 C.42种 D.56种
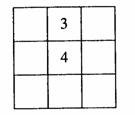 3(和平区2008年高考数学(文)三模9). 将1,2,3,…9,这9个数填在如图的9个空格中,要求每一行从左到右,每一列从上到下依次增大,当3,4固定在图中位置时,所填写空格的方法有(A )
3(和平区2008年高考数学(文)三模9). 将1,2,3,…9,这9个数填在如图的9个空格中,要求每一行从左到右,每一列从上到下依次增大,当3,4固定在图中位置时,所填写空格的方法有(A )
A. 6种 B. 12种 C.18种 D. 24种
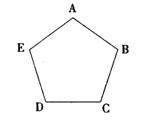
4(和平区2008年高考数学(理)三模8). 如图,正五边形ABCDE,若把顶点A、B、C、D、E染上红、黄、绿、三种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法共有( A )
A. 30种 B. 27种 C. 24种 D. 21种
1(2009年滨海新区五所重点学校联考文13).△ABC的三边长分别为AB=7,BC=5,CA=6,则 的值为____13. -19 __
的值为____13. -19 __
2(2009年滨海新区五所重点学校联考理15).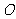 是平面上一点,
是平面上一点,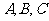 是平面上不共线三点,动点
是平面上不共线三点,动点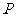 满足
满足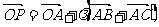 ,
,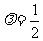 时,
则
时,
则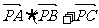 )的值为______________
0 .
)的值为______________
0 .
3(汉沽一中2008~2009届月考文12)、已知向量a=(2,3),b=(-4,7),则a在b方向上的投影为___________.
[答案]
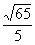
[命题意图]本题主要考查平面向量的基本概念和数量积.
[解析] ∵a·b=2×(-4)+3×7=13,|b|=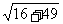 =
=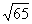
∴|a|cosθ=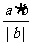 =
=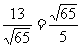
4(武清区2008~2009学年度期中理)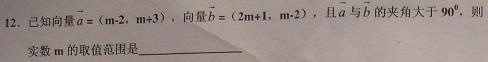
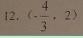
 .
.
1(汉沽一中2009届月考文3).已知平面向量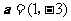 ,
,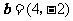 ,
,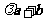 与
与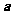 垂直,则
垂直,则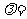 ( A )
( A )
A.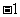 B.
B.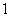 C.
C. D.
D.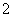
2 (汉沽一中2008~2009届月考文7).
设向量
(汉沽一中2008~2009届月考文7).
设向量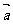 和
和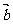 的长度分别为4和3,夹角为60°,则|
的长度分别为4和3,夹角为60°,则|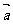 +
+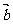 |的值为( C )
|的值为( C )
A.37
B.13
C.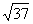 D.
D.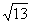
3(汉沽一中2008~2009届月考文9)、 已知平面向量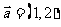 ,
, 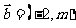 , 且
, 且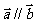 , 则
, 则
A.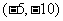 B.
B. 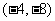 C.
C.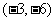 D.
D.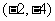
[答案]B
[命题意图]本题主要考查向量的数乘运算、加法运算、平行的充要条件以及考查学生的基本运算能力和解决问题的综合能力.
[解析1] ∵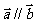 ,∴
,∴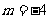 ,
,
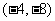
[解析2]排除法:横坐标为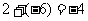 ,选B.故
,选B.故
3(汉沽一中2009届月考文3).已知平面向量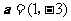 ,
,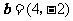 ,
,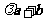 与
与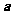 垂直,则
垂直,则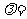 ( A )
( A )
A.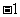 B.
B.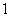 C.
C. D.
D.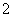
4(武清区2008~2009学年度期中理)
B
(和平区2008年高考数学(理)三模11). 如果复数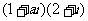 的实部和虚部相等,则实
的实部和虚部相等,则实
数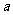 等于
。
等于
。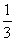

1(汉沽一中2009届月考文2).计算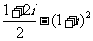 得 ( D )
得 ( D )
A.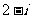 B.
B. C.
C. D.
D.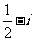
2 (2009年滨海新区五所重点学校联考理1).已知复数z =
(2009年滨海新区五所重点学校联考理1).已知复数z =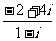 ,则z对应的点所在的象限是 (B )
,则z对应的点所在的象限是 (B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3(2009年滨海新区五所重点学校联考文2).复数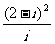 (i是虚数单位)等于 (2.D )
(i是虚数单位)等于 (2.D )
A.4+3i B.4-3i C.-4+3i D.-4-3i
4(汉沽一中2008~2009届月考文4). 复数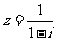 的共轭复数是( B )
的共轭复数是( B )
A.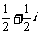 B.
B.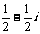 C.
C. D.
D.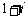
5(汉沽一中2008~2009届月考理2).复数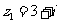 ,
,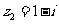 ,则复数
,则复数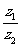 在复平面内对应的点位于 A
在复平面内对应的点位于 A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6(汉沽一中2008~2009届月考文1)、已知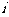 为虚数单位,则复数
为虚数单位,则复数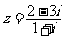 对应的点位于
对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
[答案]C
[命题意图]本题主要考查复数的实部、虚部的概念,复数的运算以及学生的运算能力.
[解析]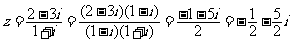
7(汉沽一中2008~2008学年月考理2).已知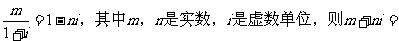 C
C
A.1+2i B. 1–2i C.2+i D.2–i
22. (本小题满分14分)
解:(1)由已知设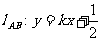 ①
①
又设抛物线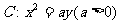 ②
②
由①②得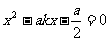 (2分)
(2分)
设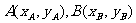 ,则
,则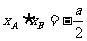
由弦长公式得
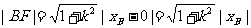 (4分)
(4分)
∴ 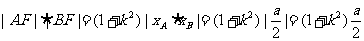
而 ,所以
,所以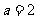
即抛物线方程为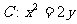 (6分)
(6分)
(2)设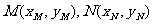
由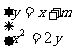
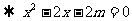
而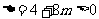
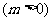
则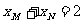 ,
,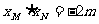 ,
,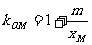 ,
,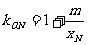 (7分)
(7分)
不妨设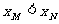 ,由于
,由于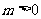 ,则
,则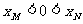
令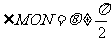 ,则ON到OM的角为
,则ON到OM的角为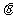 ,且满足
,且满足
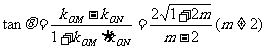 (9分)
(9分)
令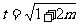 ,则
,则 ,
,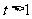 且
且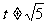 ∴
∴ 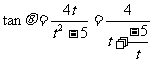 (10分)
(10分)
函数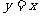 与
与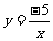 在
在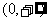 上皆为增函数
上皆为增函数
∴ 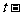
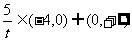
∴ 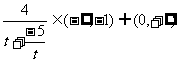 (12分)
(12分)
则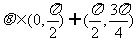 (13分)
(13分)
又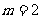 时,
时,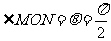
∴ 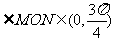 (14分)
(14分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com