
2.下列各组物质中,按熔点由低到高排列正确的是( )
A. O2 、I2、 Hg B. CO2 、KCl 、SiO2
C. Na、K、 Rb D.SiC 、 NaCl 、SO2
1.下列各组物质的晶体中,化学键类型相同、晶体类型也相同的是
A. SO2和SiO2 B. CO2和H2
C. NaCl和HCl D.CCl4和KCl
1(汉沽一中2008~2009届月考理1).设全集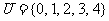 ,集合
,集合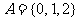 ,集合
,集合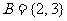 ,则
,则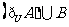 =(D)
=(D)
A.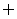 B.
B.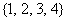 C.
C.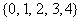 D.
D.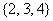
2 (汉沽一中2008~2008学年月考理1).设集合
(汉沽一中2008~2008学年月考理1).设集合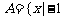 ≤x≤2},B={x|0≤x≤4},则A∩B=A
≤x≤2},B={x|0≤x≤4},则A∩B=A
A.[0,2] B.[1,2] C.[0,4] D.[1,4]
3(汉沽一中2009届月考文1).已知集合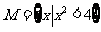 ,
,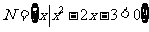 ,则集合
,则集合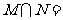 ( C )
A.
( C )
A. B.
B.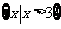 C.
C.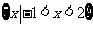 D.
D.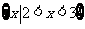
4(和平区2008年高考数学(理)三模1).设U为全集,M,P是U的两个子集,且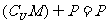 ,则
,则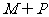 等于( D )
等于( D )
A. M B.
P C.
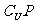 D.
D.
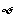
5(2009年滨海新区五所重点学校联考文1).已知:集合 ,
,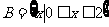 ,则
,则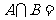 (1.C )
(1.C )
A.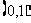 B.
B.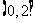 C.
C.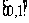 D.
D.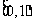
6(一中2008-2009月考理1).设集合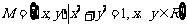 ,
,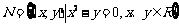 ,则
,则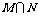 的元素个数为
的元素个数为
A.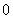 B.
B.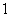 C.
C.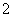 D.
D.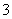 ( C )
( C )
7(汉沽一中2008~2009届月考文2).已知全集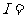 {大于
{大于 且小于10的整数},集合
且小于10的整数},集合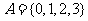 ,
,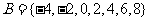 ,则集合
,则集合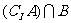 的元素个数有
的元素个数有
A.3个 B.4个 C.5个 D.6个
[答案]B
[命题意图]本题主要考查集合的表示方法、补集的概念以及集合的运算.
[解析]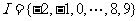 ,
,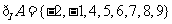
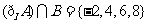 ,故集合
,故集合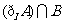 的元素个数有4个.
的元素个数有4个.
8(汉沽一中2008~2009届月考文3). “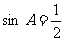 ”是“A=30º”的(B )
”是“A=30º”的(B )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9(汉沽一中2008~2009届月考文3).命题“若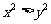 ,则
,则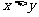 ”的逆否命题是
”的逆否命题是
A. “若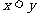 ,则
,则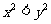 ” B. “若
” B. “若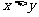 ,则
,则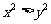 ”
”
C. “若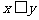 ,则
,则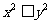 ” D. “若
” D. “若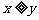 ,则
,则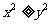 ”
”
[答案]C
[命题意图]本题主要考查命题“若P,则q”的四种形式,这是08年考纲细化的内容.
[解析]“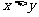 ”的否定为“
”的否定为“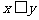 ”,“
”,“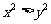 ”的否定为“
”的否定为“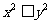 ”,所以选C.
”,所以选C.
10(汉沽一中2009届月考文5).“a=1”是“函数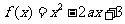 在区间[1,+∞)上为增函数”的( A
)条件
在区间[1,+∞)上为增函数”的( A
)条件
A.充分不必要 B.必要不充分 C.充要 D.不充分不必要
11 (汉沽一中2008-2009月考理2).“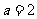 ”是“直线
”是“直线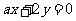 平行于直线
平行于直线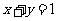 ”的
( C )
”的
( C )
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
12(2009年滨海新区五所重点学校联考理3).命题“存在x∈Z使x2+2x+m≤0”的否定是(D )
A.存在x∈Z使x2+2x+m>0 B.不存在x∈Z使x2+2x+m>0
C.对任意x∈Z使x2+2x+m≤0 D.对任意x∈Z使x2+2x+m>0
13(汉沽一中2009届月考文5).“a=1”是“函数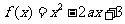 在区间[1,+∞)上为增函数”的( A )条件
在区间[1,+∞)上为增函数”的( A )条件
A.充分不必要 B.必要不充分 C.充要 D.不充分不必要
14(2009年滨海新区五所重点学校联考文9).已知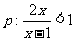 ,
,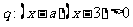 。若
。若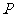 是
是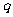 的充分不必要条件,则实数
的充分不必要条件,则实数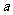 的取值范围是(9.C )
的取值范围是(9.C )
A. B.
B.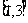
C. D.
D.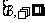
15(和平区2008年高考数学(理)三模10). 已知函数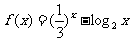 ,正实数
,正实数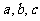 成公差为正的等差数列,且满足
成公差为正的等差数列,且满足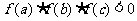 。若实数d是方程
。若实数d是方程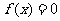 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①
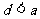 ;②
;②
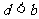 ;③
;③
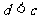 ;④
;④
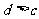 中有可能成立的个数为(B )
中有可能成立的个数为(B )
A. 1 B. 2 C. 3 D. 4
16(2009年滨海新区五所重点学校联考理16).给定下列结论:
①在区间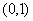 内随机地抽取两数
内随机地抽取两数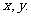 则满足
则满足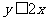 概率是
概率是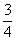 ;
;
②已知直线l1: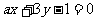 ,l2:x- by + 1= 0,则
,l2:x- by + 1= 0,则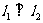 的充要条件是
的充要条件是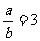 ;
;
 ③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株;
③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株;
④极坐标系内曲线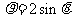 的中心
的中心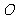 与点
与点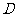
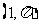 的距离为
的距离为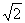 .
.
以上结论中正确的是_____________________(用序号作答) 16. ①③④
17(2009年滨海新区五所重点学校联考文16).给出下列四个命题中:
①命题“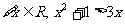 ”的否定是
”的否定是
“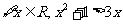 ”;
”;
②若不等式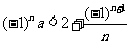 对于任意正整数
对于任意正整数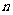 恒成立,
恒成立,
则实数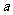 的取值范围为
的取值范围为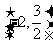 .
.
③设圆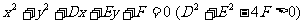 与坐标轴有4个交点,分别
与坐标轴有4个交点,分别
为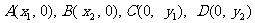 ,则
,则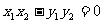 ;
;
④将函数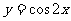 的图象向右平移
的图象向右平移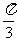 个单位,得到函数
个单位,得到函数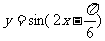
其中正确命题的序号是 16. ②③④

1(武清区2008~2009学年度期中理17)
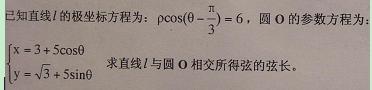

2(武清区2008~2009学年度期中理19

 .
.
 1(2009年滨海新区五所重点学校联考文)
1(2009年滨海新区五所重点学校联考文)
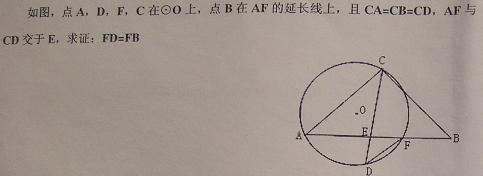
15.已知圆O直径为10,AB是圆O的直径,C为圆O上一点,
且BC=6,过点B的圆O的切线交AC延长线于点D,
则 DA=15. 12.5______;
2(汉沽一中2008~2009届月考理13).
(坐标系与参数方程选做题)在极坐标系中,
圆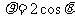 的圆心的极坐标是 ,它与方程
的圆心的极坐标是 ,它与方程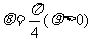 所表示的图形的交点的极坐标是
. 13.
所表示的图形的交点的极坐标是
. 13.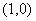 ,
,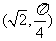 .
.
3(汉沽一中2008~2009届月考理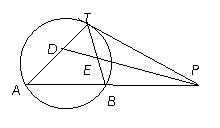 14).(几何证明选讲选做题)如图,
14).(几何证明选讲选做题)如图,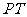 是⊙
是⊙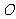 的切线,切点为
的切线,切点为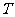 ,直线
,直线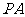 与⊙
与⊙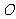 交于
交于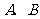 两点,
两点,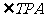 的平分线分别交直线
的平分线分别交直线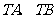 于
于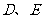 两点,已知
两点,已知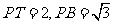 ,则
,则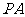 = ,
= ,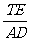 =
. 14.
=
. 14.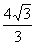 ,
,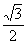 .
.
4(汉沽一中2008~2009届月考文14).(坐标系与参数方程选做题)已知点M的球坐标为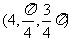 ,则它的直角坐标为____________,[答案]
,则它的直角坐标为____________,[答案]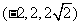
[命题意图]本题主要考查球坐标与直角坐标之间的变换关系.
[解析]由直角坐标与球坐标之间的变换关系公式求得.
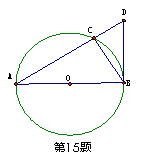
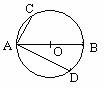 5(汉沽一中2008~2009届月考文15).(几何证明选讲选做题)如图,已知AB是⊙O的直径,AB=2,AC和AD是⊙O的两条弦,AC=
5(汉沽一中2008~2009届月考文15).(几何证明选讲选做题)如图,已知AB是⊙O的直径,AB=2,AC和AD是⊙O的两条弦,AC=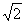 ,AD=
,AD=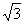 ,则∠CAD的弧度数为 .
,则∠CAD的弧度数为 .
[答案]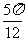
[命题意图]本题主要考查圆周角定理、直角三角形的边角关系以及考查学生添加辅助线的能力.
[解析]连结BC、BD,则∠ACB=∠ADB=90°
∵AB=2,AC=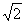 ,AD=
,AD=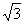 ,∴
,∴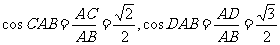 .
.
∴∠CAB= ,∠DAB=
,∠DAB=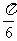 .∴∠CAD=∠CAB+∠DAB=
.∴∠CAD=∠CAB+∠DAB=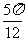 .
.
6(汉沽一中2008~2008学年月考理13).圆C: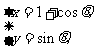 (
(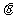 为参数)的普通方程为__________,设O为坐标原点,点M(
为参数)的普通方程为__________,设O为坐标原点,点M(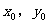 )在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。13.
)在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。13. 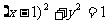 ,
,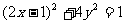
7(武清区2008~2009学年度期中理)
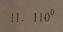
1(汉沽一中2008~2009届月考文6). 极坐标方程分别是ρ=cosθ和ρ=sinθ 的两个圆的圆心距是( D )
A.2
B.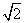 C. 1
D.
C. 1
D.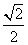
2 (武清区2008~2009学年度期中理)
(武清区2008~2009学年度期中理)

B
3(武清区2008~2009学年度期中理)
C
4(武清区2008~2009学年度期中理)
D
1(汉沽一中2008~2008学年月考理7). 已知变量a,b已被赋值,要交换a、b的值,采用的算法是D
A.a=b, b=a B.a=c, b=a, c=b C.a=c, b=a, c=a D.c=a, a=b, b=c
 2
2 (2009年滨海新区五所重点学校联考文8).某流程如右图所示,现输入如下四个函数,
(2009年滨海新区五所重点学校联考文8).某流程如右图所示,现输入如下四个函数,
则可以输出的函数是(8.D )
A.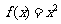 B.
B.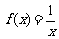
C.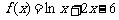 D.
D.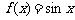
 3(汉沽一中2008~2009届月考文10). 给出下面的程序框图,那么,输出的数是(A )
3(汉沽一中2008~2009届月考文10). 给出下面的程序框图,那么,输出的数是(A )
A.2450 B. 2550
C. 5050 D. 4900
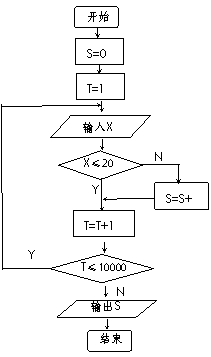 4(汉沽一中2008~2009届月考理7).为调查深圳市中学生平均每人每天参加体育锻炼时间
4(汉沽一中2008~2009届月考理7).为调查深圳市中学生平均每人每天参加体育锻炼时间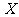 (单位:分钟),按锻炼时间分下列4种情况统计:①0-10分钟;②11-20分钟;③21-30分钟; ④30分钟以上.有10000名中学生参加了此项调查活动,右图是此次调查中某一项的流程图,其输出的结果是6200.则平均每天参加体育锻炼时间在0-20分钟内的学生的频率是(C)
(单位:分钟),按锻炼时间分下列4种情况统计:①0-10分钟;②11-20分钟;③21-30分钟; ④30分钟以上.有10000名中学生参加了此项调查活动,右图是此次调查中某一项的流程图,其输出的结果是6200.则平均每天参加体育锻炼时间在0-20分钟内的学生的频率是(C)
A.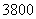
B.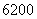
C.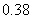
|
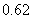
1(2009年滨海新区五所重点学校联考文19).( 本小题满分12分) 如图,在棱长为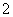 的正方体
的正方体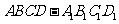 中,
中,
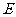 、
、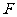 分别为
分别为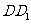 、
、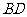 的中点。
的中点。
(Ⅰ)求证: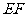 //平面
//平面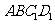
(Ⅱ)求证: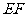 ⊥
⊥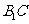
(Ⅲ)求三棱锥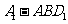 的体积
的体积
19.(本小题满分12分)
解:
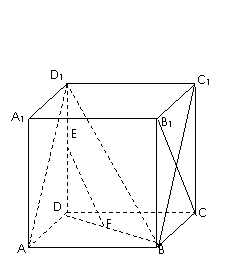 (Ⅰ)连结BD1,在△DD1B中,E、F分别为D1D,
(Ⅰ)连结BD1,在△DD1B中,E、F分别为D1D,
DB的中点,则EF//D1B。 ………………2分
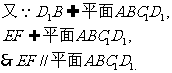
………………4分
(Ⅱ)∵B1C⊥AB,B1C⊥BC1,………………5分
AB 平面ABC1D1,BC1
平面ABC1D1,BC1 平面ABC1D1,
平面ABC1D1,
AB∩BC1=B,
∴B1C⊥平面ABC1D1。 ………………7分
又∵BD1 平面ABC1D1,
平面ABC1D1,
∴B1C⊥BD1, ………………8分
而EF//BD1,∴EF⊥B1C。………………9分
(Ⅲ)三棱锥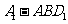 的体积
的体积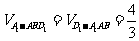 ………………12分
………………12分
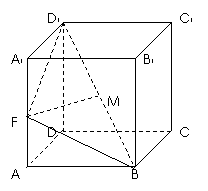 2(汉沽一中2008~2009届月考文18).(本小题满分14分)如图,已知棱柱
2(汉沽一中2008~2009届月考文18).(本小题满分14分)如图,已知棱柱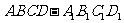 的底面是菱形,且
的底面是菱形,且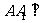 面
面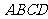 ,
,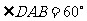 ,
,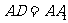 ,
,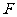 为棱
为棱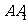 的中点,
的中点,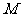 为线段
为线段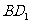 的中点,
的中点,
(1)求证: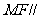 面
面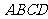 ;
;
(2)求证: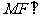 面
面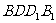 ;
;
(3)求面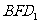 与面
与面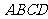 所成二面角的大小.
所成二面角的大小.
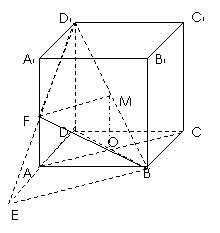 (1)证明:连结
(1)证明:连结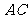 、
、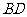 交于点
交于点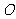 ,再连结
,再连结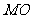 ………………………………………………1分
………………………………………………1分
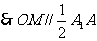 且
且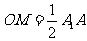 , 又
, 又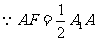 ,
,
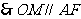 且
且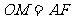
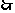 四边形
四边形 是平行四边形,
是平行四边形,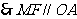 …………… 3分
…………… 3分
又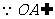 面
面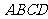
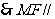 面
面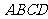 ……………………………… 4分
……………………………… 4分
(2)证明: 底面是菱形,
底面是菱形, 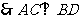 ………… 5分
………… 5分
又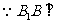 面
面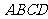 ,
,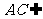 面
面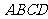
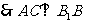 ,
,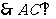 面
面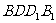 ………………………………………………6分
………………………………………………6分
又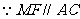
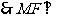 面
面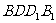 ………………………………8分
………………………………8分
(3)延长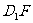 、
、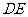 交于点
交于点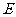 ………………………………9分
………………………………9分
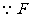 是
是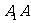 的中点且
的中点且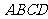 是菱形
是菱形
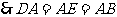
又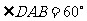
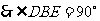 ………………………………10分
………………………………10分
由三垂线定理可知 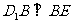
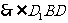 为所求角 ……………………………………………12分
为所求角 ……………………………………………12分
在菱形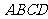 中,
中,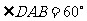
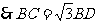
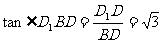
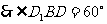 …………………………………………………14分
…………………………………………………14分
3(汉沽一中2008~2009届月考理17).(本小题满分14分)
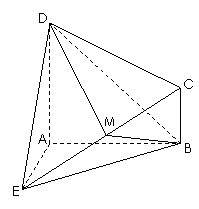 如图所示的几何体
如图所示的几何体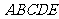 中,
中,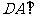 平面
平面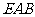 ,
,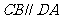 ,
,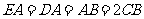 ,
,
 ,
,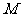 是
是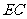 的中点.
的中点.
(Ⅰ)求证: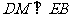 ;
;
(Ⅱ)求二面角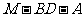 的余弦值.
的余弦值.
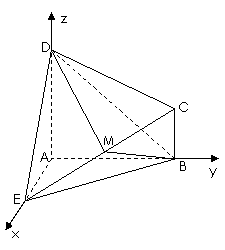 解法一: 分别以直线
解法一: 分别以直线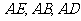 为
为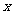 轴、
轴、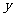 轴、
轴、 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系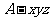 ,设
,设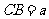 ,则
,则
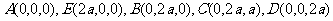 ,
,
所以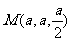 . ………………………… 4分
. ………………………… 4分
(Ⅰ)证: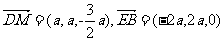 …… 5分
…… 5分
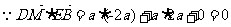 …… 6分
…… 6分
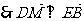 ,即
,即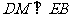 .……………………… 7分
.……………………… 7分
(Ⅱ)解:设平面 的法向量为
的法向量为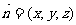 ,
,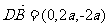
由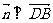 ,
,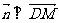 得
得
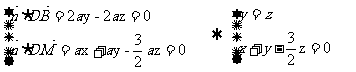
取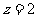 得平面
得平面 的一非零法向量为
的一非零法向量为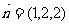 ………………………… 10分
………………………… 10分
又平面BDA的法向量为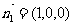 …………………………………… 11分
…………………………………… 11分
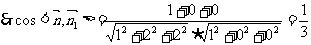 ,
,
∴二面角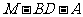 的余弦值为
的余弦值为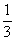 .
…………………………… 14分
.
…………………………… 14分
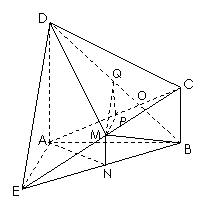 解法二:
解法二:
(Ⅰ)证明:取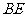 的中点
的中点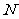 ,连接
,连接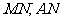 ,则
,则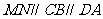 ,
,
故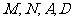 四点共面,
………………………… 2分
四点共面,
………………………… 2分
∵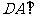 平面
平面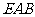 ,
,
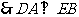 .
………………………… 3分
.
………………………… 3分
又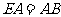
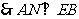 ………………………… 4分
………………………… 4分
由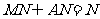 ,
,
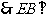 平面
平面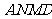 ………………………… 6分
………………………… 6分
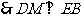 ;
……………………… 7分
;
……………………… 7分
(Ⅱ)取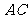 的中点
的中点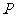 ,连
,连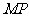 ,则
,则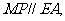
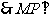 平面
平面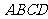
过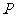 作
作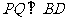 ,连
,连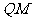 ,则
,则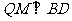
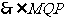 是二面角
是二面角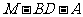 的平面角.
……………………… 9分
的平面角.
……………………… 9分
设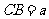 ,
, 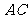 与
与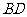 的交点为
的交点为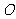 ,记
,记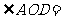
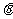 ,
,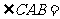
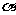 ,则有
,则有
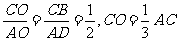
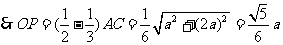 .
.
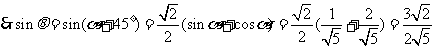 .
.
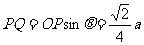 ,
…………………… 12分
,
…………………… 12分
又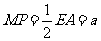
在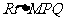 中,
中,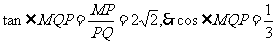
即二面角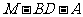 的余弦值为
的余弦值为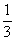 .
…………………… 14分
.
…………………… 14分
4(汉沽一中2008~2008学年月考理17).(本小题满分14分)
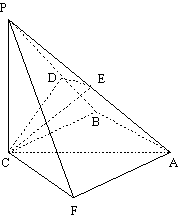
如图,三棱锥P-ABC中, PC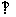 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD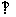 平面PAB.
平面PAB.
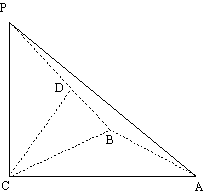 (I) 求证:AB
(I) 求证:AB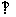 平面PCB;
平面PCB;
(II) 求异面直线AP与BC所成角的大小;
(III)求二面角C-PA-B的大小.
解法一:(I) ∵PC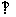 平面ABC,
平面ABC,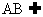 平面ABC,
平面ABC,
∴PC AB.…………………………2分
AB.…………………………2分
 ∵CD
∵CD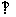 平面PAB,
平面PAB,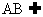 平面PAB,
平面PAB,
∴CD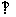 AB.…………………………4分
AB.…………………………4分
又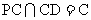 ,
,
∴AB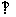 平面PCB. …………………………5分
平面PCB. …………………………5分
(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则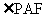 为异面直线PA与BC所成的角.………6分
为异面直线PA与BC所成的角.………6分
由(Ⅰ)可得AB⊥BC,
∴CF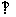 AF.
AF.
由三垂线定理,得PF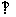 AF.
AF.
则AF=CF= ,PF=
,PF=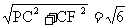 ,
,
在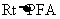 中, tan∠PAF=
中, tan∠PAF=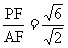 =
= ,
,
∴异面直线PA与BC所成的角为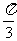 .…………………………………9分
.…………………………………9分
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE 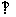 PA,CE=
PA,CE= .
.
∵CD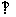 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE 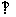 PA.
PA.
∴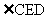 为二面角C-PA-B的平面角.…………………………………11分
为二面角C-PA-B的平面角.…………………………………11分
由(I) AB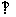 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC= .
.
在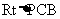 中,PB=
中,PB=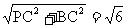 ,
,
 .
.
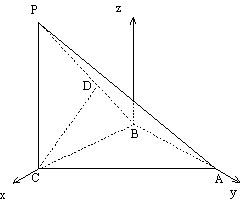 在
在 中, sin∠CED=
中, sin∠CED=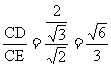 .
.
∴二面角C-PA-B的大小为arcsin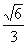 .……14分
.……14分
解法二:(I)同解法一.
(II) 由(I) AB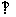 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC= .
.
以B为原点,如图建立坐标系.
则A(0, ,0),B(0,0,0),
,0),B(0,0,0),
C( ,0,0),P(
,0,0),P( ,0,2).
,0,2).
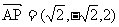 ,
,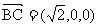 .
.
…………………7分
则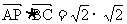 +0+0=2.
+0+0=2.
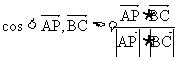 =
=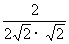 =
= 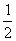 .
.
∴异面直线AP与BC所成的角为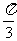 .………………………10分
.………………………10分
(III)设平面PAB的法向量为m= (x,y,z).
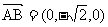 ,
,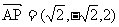 ,
,
则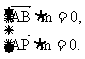 即
即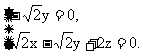

解得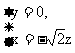 令
令 = -1, 得
m= (
= -1, 得
m= ( ,0,-1).
,0,-1).
设平面PAC的法向量为n=(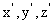 ).
).
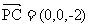 ,
,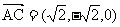 ,
,
则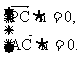 即
即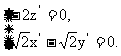
解得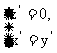 令
令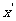 =1, 得
n= (1,1,0).……………………………12分
=1, 得
n= (1,1,0).……………………………12分
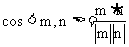 =
=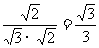 .
.
∴二面角C-PA-B的大小为arccos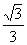 .………………………………14分
.………………………………14分
5(和平区2008年高考数学(理)三模19). (本小题满分12分)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE。
(1)求证:AE⊥平面BCE;
(2)求二面角B-AC-E的大小;
(3)求点D到平面ACE的距离。
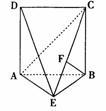
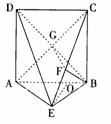
解:(1)如图,∵ BF⊥平面ACE ∴ BF⊥AE(1分)
又∵ 二面角D-AB-E为直二面角,且CB⊥AB
∴ CB⊥平面ABE ∴ CB⊥AE
∵ 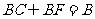 ∴ AE⊥平面BCE(3分)
∴ AE⊥平面BCE(3分)
(2)连BD交AC于G,连FG
∵ 正方形ABCD边长为2 ∴ BG⊥AC,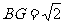
∵ BF⊥平面ACE 由三垂线定理逆定理得FG⊥AC
∴ ∠BGF是二面角B-AC-E的平面角(5分)
由(1)AE⊥平面BCE ∴ AE⊥EB
又∵ AE=EB ∴
在等腰直角三角形AEB中,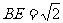
又∵ Rt△BCE中,
∴ 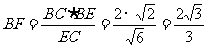 (7分)
(7分)
∴ 在Rt△BFG中,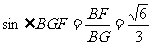
∴ 二面角B-AC-E等于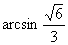 (8分)
(8分)
(3)过E作EO⊥AB于O,OE=1
∵ 二面角D-AB-E为直二面角
∴ EO⊥平面ABCD(9分)
设D到平面ACE的距离为h
∵ 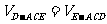 ∴
∴ 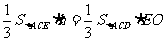
∵ AE⊥平面BCE ∴ AE⊥EC
∴ 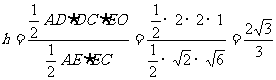
∴ 点D到平面ACE的距离为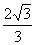 (12分)
(12分)

1(汉沽一中2008~2009届月考理11).在直角三角形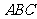 中,两直角边分别为
中,两直角边分别为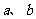 ,设
,设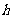 为斜边上的高,则
为斜边上的高,则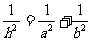 ,由此类比:三棱锥
,由此类比:三棱锥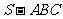 的三个侧棱
的三个侧棱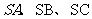 两两垂直,且长分别为
两两垂直,且长分别为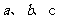 ,设棱锥底面
,设棱锥底面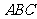 上的高为
上的高为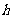 ,则
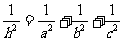
.
,则
. 
2(汉沽一中2008~2008学年月考理11).一个正四棱锥的底面边长为2,侧棱长为 ,五个顶点都在同一个球面上,则此球的表面积为
. 9π
,五个顶点都在同一个球面上,则此球的表面积为
. 9π
3(和平区2008年高考数学(理)三模12). 在120°的二面角内放一个半径为6的球,与两个半平面各有且仅有一个公共点,则这两点间的球面距离是 。2
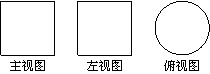
1(汉沽一中2008~2009届月考理 3).如右图所示,一个空间几何体的主视图和左视图都是边长为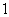 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为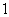 的圆,那么这个几何体的全面积为(A)
的圆,那么这个几何体的全面积为(A)
 A.
A.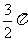 B.
B.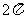
C.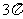 D.
D.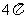
2 (汉沽一中2008~2009届月考文5). 一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是( C )
(汉沽一中2008~2009届月考文5). 一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是( C )
A.异面 B. 相交 C. 平行 D. 不确定
3(和平区2008年高考数学(理)三模6). 如果直线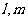 与平面
与平面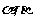 ,
, 满足:
满足: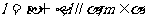 和
和 ,那么必有(B )
,那么必有(B )
A. 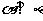 且
且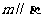 B.
B.
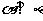 且
且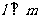
C. 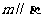 且
且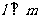 D.
D.
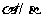 且
且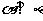
4(汉沽一中2008~2008学年月考理6).三棱锥D-ABC的三个侧面分别与底面全等,且AB=AC= ,BC=2,则二面角A-BC-D的大小为D
,BC=2,则二面角A-BC-D的大小为D
A. 300 B. 450 C.600 D.900
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com