
18.(16分)过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为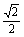 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=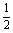 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
解 设椭圆C的方程为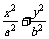 =1(a>b>0),显然,直线l的斜率存在且不为0,设l的方程为y=k(x-1)代入椭圆方程,整理得
=1(a>b>0),显然,直线l的斜率存在且不为0,设l的方程为y=k(x-1)代入椭圆方程,整理得
(k2a2+b2)x2-2k2a2x+a2k2-a2b2=0.
因为直线l与C交于A、B两点
∴Δ=4k4a4-4(a2k2-a2b2)(k2a2+b2)>0.
即k2a2-k2+b2>0, ①
当Δ>0时,设直线l与椭圆C的交点为
A(x1,y1)、B(x2,y2),AB中点为M(x0,y0),则
x0=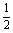 (x1+x2)=
(x1+x2)=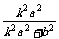
∴y0=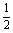 (y1+y2)=
(y1+y2)= 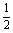 [k(x1-1)+k(x2-1)]
[k(x1-1)+k(x2-1)]
=-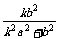 .
.
∵M(x0,y0)在直线y=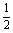 x上,
x上,
∴-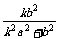 =
=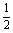 ·
·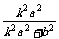 ,
,
∴k=-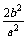 .又
.又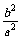 =1-e2=1-
=1-e2=1-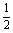 =
=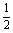 ,
,
∴k=-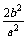 =-1.
=-1.
因此直线l的方程为y=-x+1.
∵a2=2b2,∴椭圆C的方程为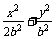 =1,其右焦点为(b,0),设(b,0)点关于直线y=-x+1的对称点为(x′,y′),
=1,其右焦点为(b,0),设(b,0)点关于直线y=-x+1的对称点为(x′,y′),
则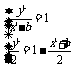

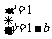 .
.
因为点(1,1-b)在椭圆上.
∴1+2(1-b)2=2b2,解得b2=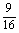 .
.
把b2=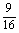 ,a2=
,a2=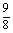 ,k2=1代入①式,得Δ>0.
,k2=1代入①式,得Δ>0.
∴b2=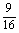 ,a2=
,a2=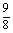 .
.
∴椭圆C的方程为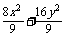 =1,
=1,
直线l的方程为y=-x+1.
17.(14分)已知双曲线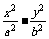 =1的右焦点是F,右顶点是A,虚轴的上端点是B,
=1的右焦点是F,右顶点是A,虚轴的上端点是B,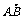 ·
·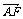 =6-4
=6-4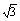 ,∠BAF=150°.
,∠BAF=150°.
(1)求双曲线的方程;
(2)设Q是双曲线上的点,且过点F、Q的直线l与y轴交于点M,若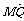 +2
+2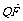 =0,求直线l的斜率.
=0,求直线l的斜率.
解 (1)由条件知A(a,0),B(0,b),F(c,0)
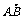 ·
·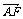 =(-a, b)·(c-a,0)=a(a-c)=6-4
=(-a, b)·(c-a,0)=a(a-c)=6-4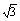
|
|
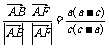
=-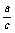 =cos150°=-
=cos150°=-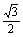 .
.
∴a=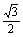 c,代入a(a-c)=6-4
c,代入a(a-c)=6-4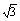 中得c=2
中得c=2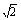 .
.
∴a=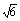 ,b2=c2-a2=2,故双曲线的方程为
,b2=c2-a2=2,故双曲线的方程为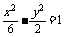 .
.
(2)∵点F的坐标为(2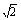 ,0).
,0).
∴可设直线l的方程为y=k(x-2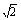 ),
),
令x=0,得y=-2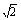 k,即M(0,-2
k,即M(0,-2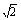 k)
k)
设Q(m,n),则由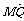 +2
+2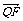 =0得
=0得
(m,n+2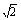 k)+2(2
k)+2(2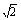 -m,-n)=(0,0).
-m,-n)=(0,0).
即(4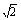 -m,2
-m,2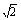 k-n)=(0,0).
k-n)=(0,0).
即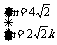 ,∵
,∵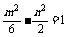 .
.
∴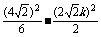 =1,得k2=
=1,得k2=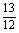 ,k=±
,k=±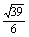 .
.
16.(14分)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
解 (1)(x-1)2+(y-2)2=5-m,∴m<5.
(2)设M(x1,y1),N(x2,y2),
则x1=4-2y1,x2=4-2y2,
则x1x2=16-8(y1+y2)+4y1y2
∵OM⊥ON,∴x1x2+y1y2=0
∴16-8(y1+y2)+5y1y2=0 ①
由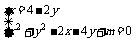
得5y2-16y+m+8=0
∴y1+y2=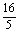 ,y1y2=
,y1y2=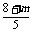 ,代入①得,m=
,代入①得,m=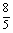 .
.
(3)以MN为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0
即x2+y2-(x1+x2)x-(y1+y2)y=0
∴所求圆的方程为x2+y2-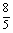 x-
x-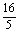 y=0.
y=0.
15.(14分)过点M(0,1)作直线,使它被直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M平分,求此直线方程.
解 方法一 过点M且与x轴垂直的直线是y轴,它和两已知直线的交点分别是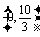 和(0,8),显然不满足中点是点
和(0,8),显然不满足中点是点
M(0,1)的条件.
故可设所求直线方程为y=kx+1,与已知两直线l1,l2分别交于A、B两点,联立方程组
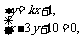 ①
①
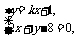 ②
②
由①解得xA=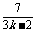 ,由②解得xB=
,由②解得xB=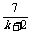 .
.
∵点M平分线段AB,
∴xA+xB=2xM,即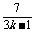 +
+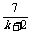 =0.
=0.
解得k=-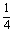 ,故所求直线方程为x+4y-4=0.
,故所求直线方程为x+4y-4=0.
方法二 设所求直线与已知直线l1,l2分别交于A、B两点.
∵点B在直线l2:2x+y-8=0上,
故可设B(t,8-2t),M(0,1)是AB的中点.
由中点坐标公式得A(-t,2t-6).
∵A点在直线l1:x-3y+10=0上,
∴(-t)-3(2t-6)+10=0,解得t=4.
∴B(4,0),A(-4,2),故所求直线方程为x+4y-4=0.
14.已知两点A(1,0),B(b,0),若抛物线y2=4x上存在点C使△ABC为等边三角形,则b= .
答案 5或-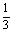
13.在平面直角坐标系xOy中,已知△ABC顶点A(-4,0)和C(4,0),顶点B在椭圆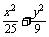 =1上,则
=1上,则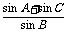 =
.
=
.
答案 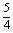
12.已知F1、F2为椭圆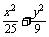 =1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=12,则|AB|= .
=1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=12,则|AB|= .
答案 8
11.(2009·东海高级中学高三调研)两个正数m,n的等差中项是5,等比中项是4,若m>n,则椭圆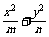 =1的离心率e的大小为
.
=1的离心率e的大小为
.
答案 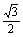
10.设P为双曲线x2-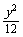 =1上的一点,F1、F2是该双曲线的两个焦点.若|PF1|∶|PF2|=3∶2,则△PF1F2的面积为 .
=1上的一点,F1、F2是该双曲线的两个焦点.若|PF1|∶|PF2|=3∶2,则△PF1F2的面积为 .
答案 12
9.(2008·山东理)已知圆的方程为x2+y2-6x-8y=0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为 .
答案 20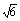
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com