
5.等比数列的性质:
(1)当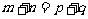 时,则有
时,则有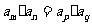 ,特别地,当
,特别地,当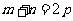 时,则有
时,则有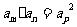 .如(1)在等比数列
.如(1)在等比数列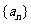 中,
中,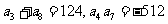 ,公比q是整数,则
,公比q是整数,则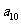 =___(答:512);(2)各项均为正数的等比数列
=___(答:512);(2)各项均为正数的等比数列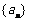 中,若
中,若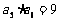 ,则
,则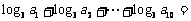 (答:10)。
(答:10)。
(2) 若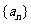 是等比数列,则
是等比数列,则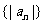 、
、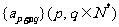 、
、 成等比数列;若
成等比数列;若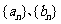 成等比数列,则
成等比数列,则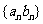 、
、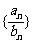 成等比数列; 若
成等比数列; 若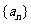 是等比数列,且公比
是等比数列,且公比 ,则数列
,则数列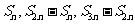 ,…也是等比数列。当
,…也是等比数列。当 ,且
,且 为偶数时,数列
为偶数时,数列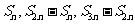 ,…是常数数列0,它不是等比数列. 如(1)已知
,…是常数数列0,它不是等比数列. 如(1)已知 且
且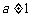 ,设数列
,设数列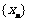 满足
满足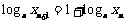
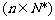 ,且
,且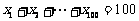 ,则
,则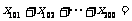 . (答:
. (答: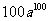 );(2)在等比数列
);(2)在等比数列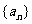 中,
中,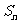 为其前n项和,若
为其前n项和,若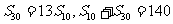 ,则
,则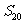 的值为______(答:40)
的值为______(答:40)
(3)若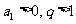 ,则
,则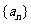 为递增数列;若
为递增数列;若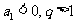 , 则
, 则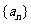 为递减数列;若
为递减数列;若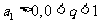 ,则
,则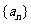 为递减数列;若
为递减数列;若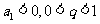 , 则
, 则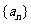 为递增数列;若
为递增数列;若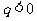 ,则
,则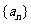 为摆动数列;若
为摆动数列;若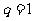 ,则
,则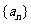 为常数列.
为常数列.
(4) 当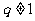 时,
时,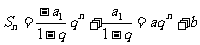 ,这里
,这里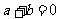 ,但
,但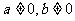 ,这是等比数列前
,这是等比数列前 项和公式的一个特征,据此很容易根据
项和公式的一个特征,据此很容易根据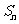 ,判断数列
,判断数列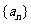 是否为等比数列。如若
是否为等比数列。如若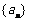 是等比数列,且
是等比数列,且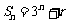 ,则
,则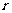 =
(答:-1)
=
(答:-1)
(5) 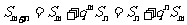 .如设等比数列
.如设等比数列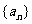 的公比为
的公比为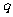 ,前
,前 项和为
项和为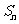 ,若
,若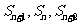 成等差数列,则
成等差数列,则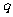 的值为_____(答:-2)
的值为_____(答:-2)
(6) 在等比数列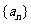 中,当项数为偶数
中,当项数为偶数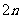 时,
时,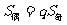 ;项数为奇数
;项数为奇数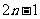 时,
时,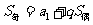 .
.
(7)如果数列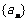 既成等差数列又成等比数列,那么数列
既成等差数列又成等比数列,那么数列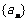 是非零常数数列,故常数数列
是非零常数数列,故常数数列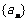 仅是此数列既成等差数列又成等比数列的必要非充分条件。如设数列
仅是此数列既成等差数列又成等比数列的必要非充分条件。如设数列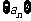 的前
的前 项和为
项和为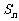 (
(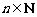 ), 关于数列
), 关于数列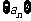 有下列三个命题:①若
有下列三个命题:①若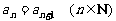 ,则
,则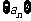 既是等差数列又是等比数列;②若
既是等差数列又是等比数列;②若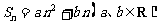 ,则
,则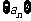 是等差数列;③若
是等差数列;③若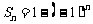 ,则
,则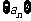 是等比数列。这些命题中,真命题的序号是
(答:②③)
是等比数列。这些命题中,真命题的序号是
(答:②③)
4.等比数列的有关概念:
(1)等比数列的判断方法:定义法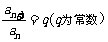 ,其中
,其中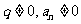 或
或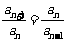
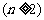 。如(1)一个等比数列{
。如(1)一个等比数列{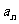 }共有
}共有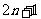 项,奇数项之积为100,偶数项之积为120,则
项,奇数项之积为100,偶数项之积为120,则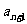 为____(答:
为____(答: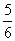 );(2)数列
);(2)数列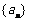 中,
中,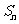 =4
=4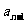 +1 (
+1 (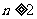 )且
)且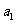 =1,若
=1,若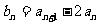 ,求证:数列{
,求证:数列{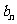 }是等比数列。
}是等比数列。
(2)等比数列的通项: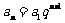 或
或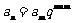 。如设等比数列
。如设等比数列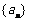 中,
中,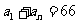 ,
,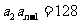 ,前
,前 项和
项和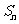 =126,求
=126,求 和公比
和公比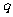 . (答:
. (答: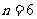 ,
,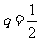 或2)
或2)
(3)等比数列的前 和:当
和:当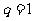 时,
时,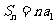 ;当
;当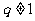 时,
时,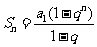
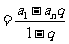 。如(1)等比数列中,
。如(1)等比数列中,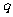 =2,S99=77,求
=2,S99=77,求 (答:44);(2)
(答:44);(2)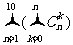 的值为__________(答:2046);
的值为__________(答:2046);
特别提醒:等比数列前 项和公式有两种形式,为此在求等比数列前
项和公式有两种形式,为此在求等比数列前 项和时,首先要判断公比
项和时,首先要判断公比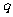 是否为1,再由
是否为1,再由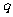 的情况选择求和公式的形式,当不能判断公比
的情况选择求和公式的形式,当不能判断公比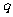 是否为1时,要对
是否为1时,要对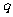 分
分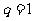 和
和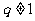 两种情形讨论求解。
两种情形讨论求解。
(4)等比中项:若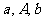 成等比数列,那么A叫做
成等比数列,那么A叫做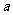 与
与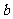 的等比中项。提醒:不是任何两数都有等比中项,只有同号两数才存在等比中项,且有两个
的等比中项。提醒:不是任何两数都有等比中项,只有同号两数才存在等比中项,且有两个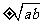 。如已知两个正数
。如已知两个正数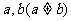 的等差中项为A,等比中项为B,则A与B的大小关系为______(答:A>B)
的等差中项为A,等比中项为B,则A与B的大小关系为______(答:A>B)
提醒:(1)等比数列的通项公式及前 和公式中,涉及到5个元素:
和公式中,涉及到5个元素: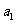 、
、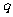 、
、 、
、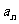 及
及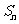 ,其中
,其中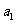 、
、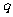 称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2;(2)为减少运算量,要注意设元的技巧,如奇数个数成等比,可设为…,
称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2;(2)为减少运算量,要注意设元的技巧,如奇数个数成等比,可设为…,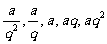 …(公比为
…(公比为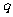 );但偶数个数成等比时,不能设为…
);但偶数个数成等比时,不能设为…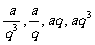 ,…,因公比不一定为正数,只有公比为正时才可如此设,且公比为
,…,因公比不一定为正数,只有公比为正时才可如此设,且公比为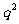 。如有四个数,其中前三个数成等差数列,后三个成等比数列,且第一个数与第四个数的和是16,第二个数与第三个数的和为12,求此四个数。(答:15,,9,3,1或0,4,8,16)
。如有四个数,其中前三个数成等差数列,后三个成等比数列,且第一个数与第四个数的和是16,第二个数与第三个数的和为12,求此四个数。(答:15,,9,3,1或0,4,8,16)
3.等差数列的性质:
(1)当公差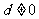 时,等差数列的通项公式
时,等差数列的通项公式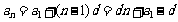 是关于
是关于 的一次函数,且斜率为公差
的一次函数,且斜率为公差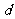 ;前
;前 和
和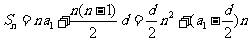 是关于
是关于 的二次函数且常数项为0.
的二次函数且常数项为0.
(2)若公差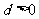 ,则为递增等差数列,若公差
,则为递增等差数列,若公差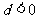 ,则为递减等差数列,若公差
,则为递减等差数列,若公差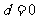 ,则为常数列。
,则为常数列。
(3)当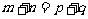 时,则有
时,则有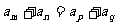 ,特别地,当
,特别地,当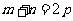 时,则有
时,则有 .如(1)等差数列
.如(1)等差数列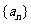 中,
中,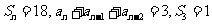 ,则
,则 =____(答:27);(2)在等差数列
=____(答:27);(2)在等差数列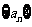 中,
中,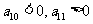 ,且
,且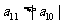 ,
,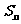 是其前
是其前 项和,则A、
项和,则A、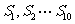 都小于0,
都小于0,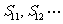 都大于0 B、
都大于0 B、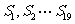 都小于0,
都小于0,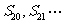 都大于0 C、
都大于0 C、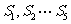 都小于0,
都小于0,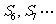 都大于0 D、
都大于0 D、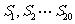 都小于0,
都小于0,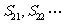 都大于0 (答:B)
都大于0 (答:B)
(4) 若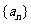 、
、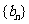 是等差数列,则
是等差数列,则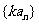 、
、 (
( 、
、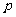 是非零常数)、
是非零常数)、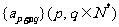 、
、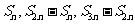 ,…也成等差数列,而
,…也成等差数列,而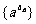 成等比数列;若
成等比数列;若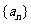 是等比数列,且
是等比数列,且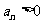 ,则
,则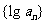 是等差数列. 如等差数列的前n项和为25,前2n项和为100,则它的前3n和为
。(答:225)
是等差数列. 如等差数列的前n项和为25,前2n项和为100,则它的前3n和为
。(答:225)
(5)在等差数列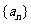 中,当项数为偶数
中,当项数为偶数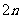 时,
时,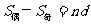 ;项数为奇数
;项数为奇数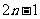 时,
时,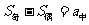 ,
,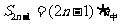 (这里
(这里 即
即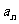 );
);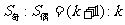 。如(1)在等差数列中,S11=22,则
。如(1)在等差数列中,S11=22,则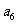 =______(答:2);(2)项数为奇数的等差数列
=______(答:2);(2)项数为奇数的等差数列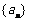 中,奇数项和为80,偶数项和为75,求此数列的中间项与项数(答:5;31).
中,奇数项和为80,偶数项和为75,求此数列的中间项与项数(答:5;31).
(6)若等差数列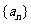 、
、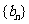 的前
的前 和分别为
和分别为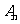 、
、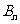 ,且
,且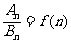 ,则
,则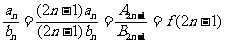 .如设{
.如设{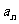 }与{
}与{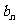 }是两个等差数列,它们的前
}是两个等差数列,它们的前 项和分别为
项和分别为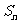 和
和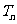 ,若
,若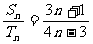 ,那么
,那么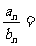 ___________(答:
___________(答: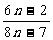 )
)
(7)“首正”的递减等差数列中,前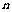 项和的最大值是所有非负项之和;“首负”的递增等差数列中,前
项和的最大值是所有非负项之和;“首负”的递增等差数列中,前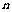 项和的最小值是所有非正项之和。法一:由不等式组
项和的最小值是所有非正项之和。法一:由不等式组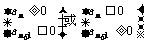 确定出前多少项为非负(或非正);法二:因等差数列前
确定出前多少项为非负(或非正);法二:因等差数列前 项是关于
项是关于 的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性
的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性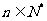 。上述两种方法是运用了哪种数学思想?(函数思想),由此你能求一般数列中的最大或最小项吗?如(1)等差数列
。上述两种方法是运用了哪种数学思想?(函数思想),由此你能求一般数列中的最大或最小项吗?如(1)等差数列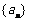 中,
中,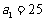 ,
,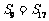 ,问此数列前多少项和最大?并求此最大值。(答:前13项和最大,最大值为169);(2)若
,问此数列前多少项和最大?并求此最大值。(答:前13项和最大,最大值为169);(2)若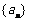 是等差数列,首项
是等差数列,首项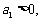
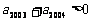 ,
,
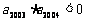 ,则使前n项和
,则使前n项和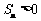 成立的最大正整数n是
(答:4006)
成立的最大正整数n是
(答:4006)
(8)如果两等差数列有公共项,那么由它们的公共项顺次组成的新数列也是等差数列,且新等差数列的公差是原两等差数列公差的最小公倍数. 注意:公共项仅是公共的项,其项数不一定相同,即研究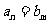 .
.
2.等差数列的有关概念:
(1)等差数列的判断方法:定义法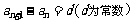 或
或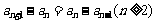 。如设
。如设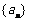 是等差数列,求证:以bn=
是等差数列,求证:以bn=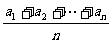
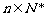 为通项公式的数列
为通项公式的数列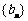 为等差数列。
为等差数列。
(2)等差数列的通项: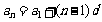 或
或 。如(1)等差数列
。如(1)等差数列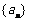 中,
中,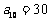 ,
,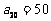 ,则通项
,则通项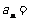 (答:
(答: );(2)首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是______(答:
);(2)首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是______(答: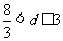 )
)
(3)等差数列的前 和:
和: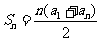 ,
,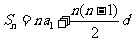 。如(1)数列
。如(1)数列 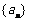 中,
中,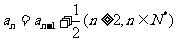 ,
,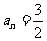 ,前n项和
,前n项和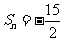 ,则
,则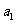 =_,
=_, =_(答:
=_(答: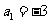 ,
,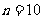 );(2)已知数列
);(2)已知数列 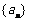 的前n项和
的前n项和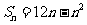 ,求数列
,求数列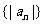 的前
的前 项和
项和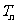 (答:
(答: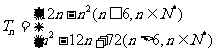 ).
).
(4)等差中项:若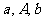 成等差数列,则A叫做
成等差数列,则A叫做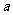 与
与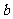 的等差中项,且
的等差中项,且 。
。
提醒:(1)等差数列的通项公式及前 和公式中,涉及到5个元素:
和公式中,涉及到5个元素: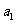 、
、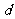 、
、 、
、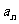 及
及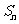 ,其中
,其中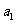 、
、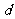 称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。(2)为减少运算量,要注意设元的技巧,如奇数个数成等差,可设为…,
称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。(2)为减少运算量,要注意设元的技巧,如奇数个数成等差,可设为…,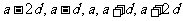 …(公差为
…(公差为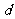 );偶数个数成等差,可设为…,
);偶数个数成等差,可设为…,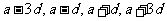 ,…(公差为2
,…(公差为2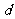 )
)
1、数列的概念:数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式。如(1)已知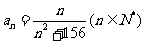 ,则在数列
,则在数列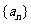 的最大项为__(答:
的最大项为__(答: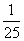 );(2)数列
);(2)数列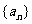 的通项为
的通项为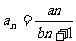 ,其中
,其中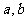 均为正数,则
均为正数,则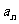 与
与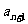 的大小关系为___(答:
的大小关系为___(答: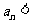
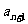 );(3)已知数列
);(3)已知数列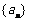 中,
中,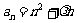 ,且
,且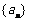 是递增数列,求实数
是递增数列,求实数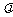 的取值范围(答:
的取值范围(答: );(4)一给定函数
);(4)一给定函数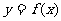 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意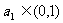 ,由关系式
,由关系式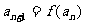 得到的数列
得到的数列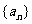 满足
满足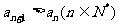 ,则该函数的图象是 ()(答:A)
,则该函数的图象是 ()(答:A)
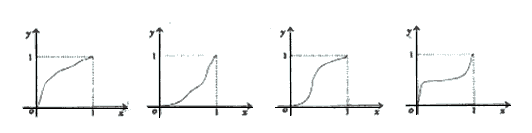
A B C D
1、直抒胸臆:直接运用抒情与议论的表达方式来抒发情感
2.运用具体描写手段:语言描写、动作描写、神态描写、外貌描写、心理描写、细节描写
⒊运用修辞手法来写人:比喻对比夸张比拟借代双关反问设问、反问、反语;
⒋运用表现手法来写:衬托对比渲染烘托象征、铺陈,白描。
第三种:抒情方式
5.从观察的层次来写:远看与近观结合,仰视平视与俯视结合;空间的上下结合,高低结合。
⒍从调动感觉的角度来写:视觉(形和色),听觉(声),嗅觉(气味),味觉,触觉;或通感。
第二种:描写人物的方法
⒈从直接与间接的角度看,方法有:正面和侧面描写,虚写(想象联想)与实写;
4.从景物的动静角度来写:动景静景结合,或以动写静,以静写动;(高考常考)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com