
4.对较复杂的不等式先用分析法探求证明途径,再用综合法,或比较法加以证明。
3. 分析法:从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能够肯定这些条件都已具备,那么就可以判定所证的不等式成立。这种证明方法叫做分析法。要注意书写的格式, 综合法是分析法的逆过程
2. 综合法:利用某些已经证明过的不等式(如均值不等式,常用不等式,函数单调性)作为基础,再运用不等式的性质推导出所要证的不等式的方法。
1. 比较法证明不等式是最基本的方法也是最常用的方法。比较法的两种形式:
(1)比差法:步骤是:①作差;②分解因式或配方;③判断差式符号;
(2)比商法:要证a>b且b>0,只须证 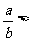 1。
1。
说明:①作差比较法证明不等式时,通常是进行通分、因式分解或配方,利用各因式的符号或非负数的性质进行判断;
②证幂、乘积的不等式时常用比商法,证对数不等式时常用比差法。运用比商法时必须确定两式的符号;
2.掌握分析法、综合法、比较法证明简单的不等式。
1.理解不等式的性质和证明;
10. (2005福建) 已知函数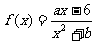 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
解:(1)由函数f(x)的图象在点M(-1f(-1))处的 切线方程为x+2y+5=0,知

解是a=2,b=3,(∵b+1≠0,b=-1舍去)
所求的函数解析式是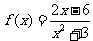
(II)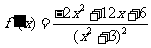 ,令-2x2+12x+6=0,解得
,令-2x2+12x+6=0,解得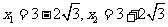 。
。
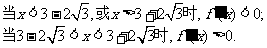
∴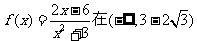 内是减函数,在
内是减函数,在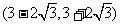 内是增函数,在
内是增函数,在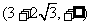 内是减函数。
内是减函数。
考查知识:函数的单调性,导数的应用等知识,考查运用数学知识,分析问题和解决问题的能力.
[探索题](2006福建) 已知函数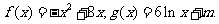
(I)求f(x)在区间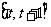 上的最大值h(t)
上的最大值h(t)
(II)是否存在实数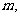 使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出
使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出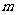 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(I)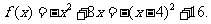
当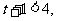 即
即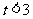 时,f(x)在
时,f(x)在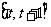 上单调递增,
上单调递增,
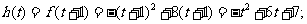
当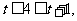 即
即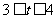 时,
时,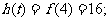
当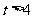 时,f(x)在
时,f(x)在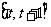 上单调递减,
上单调递减,
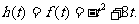
综上,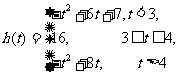
(II)函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点,即函数
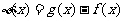 的图象与x轴的正半轴有且只有三个不同的交点。
的图象与x轴的正半轴有且只有三个不同的交点。
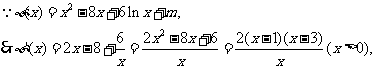
当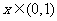 时,
时,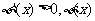 是增函数;
是增函数;
当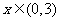 时,
时,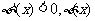 是减函数;
是减函数;
当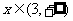 时,
时,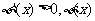 是增函数;
是增函数;
当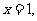 或
或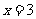 时,
时,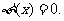
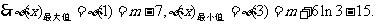
 当
当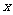 充分接近0时,
充分接近0时,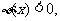 当
当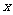 充分大时,
充分大时,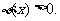
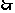 要使
要使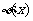 的图象与
的图象与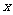 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
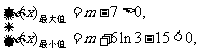 即
即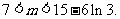
所以存在实数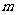 ,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)
,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)
9. (2006山东)设函数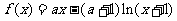 ,其中
,其中 ,求f(x)的单调区间.
,求f(x)的单调区间.
解:由已知得函数f(x)的定义域为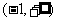 ,且
,且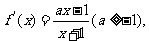
(1)当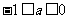 时,f′(x)<0函数f(x)在
时,f′(x)<0函数f(x)在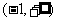 上单调递减,
上单调递减,
(2)当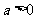 时,由f′(x)=0解得
时,由f′(x)=0解得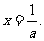
若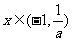 ,则f′(x)<0函数f(x)在
,则f′(x)<0函数f(x)在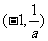 上单调递减.
上单调递减.
若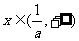 则,f′(x)>0函数f(x)在
则,f′(x)>0函数f(x)在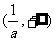 上单调递增.
上单调递增.
综上所述:
当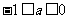 时,函数f(x)在(-1,+∞)上单调递减.
时,函数f(x)在(-1,+∞)上单调递减.
当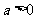 时,函数f(x)在
时,函数f(x)在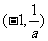 上单调递减,函数f(x)在
上单调递减,函数f(x)在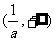 上单调递增.
上单调递增.
8. (2005北京)
已知函数f(x)= -x3+3x2+9x+a
(Ⅰ)求f(x)的单调减区间;
(Ⅱ)若f(x)在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
解:(I)f′(x)= -3x2+6x+9 令f′(x)<0,解得x<-1或x>3
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞)
(II)因为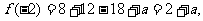

所以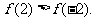
因为在(-1,3)上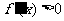 ,所以f(x)在[-1,2]上单调递增,又由于f(x)在
,所以f(x)在[-1,2]上单调递增,又由于f(x)在
[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和
最小值.
于是有22+a=20,解得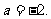 a=-2
a=-2
故f(x)= -x3+3x2+9x-2 因此f(-1)=1+3-9-2=-7
即函数f(x)在区间[-2,2]上的最小值为-7.
7.(2006北京)
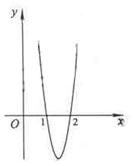
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(0,1),(2,0),如图所示.求:
 (Ⅰ)x0的值;
(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
解法一:
(Ⅰ)由图像可知,在(-∞,1)上f′(x)>0,在(1,2)上f′(x)<0,在(2,+∞)上f′(x)>0
故f(x)在(-∞,1), (2,+∞)上递增,在(1,2) 上递减,
因此f(x)在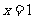 处取得极大值,所以
处取得极大值,所以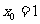
(Ⅱ)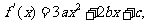
由f′(1)=0, f′(2)=0, f(1)=5
得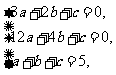
解得a=2, b= -9, c=12.
解法二:
(Ⅰ)同解法一
(Ⅱ)设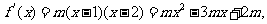
又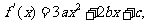
所以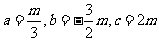
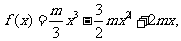
由f(1)=5,即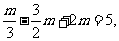 得m=6
得m=6
所以a=2,b=-9,c=12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com