
2.(2008·全国Ⅰ理,8)为得到函数y=cos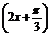 的图象,只需将函数y=sin2x的图象向
平移 个单位长度.
的图象,只需将函数y=sin2x的图象向
平移 个单位长度.
答案 左 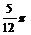
1.某三角函数图象的一部分如下图所示,则该三角函数为 .
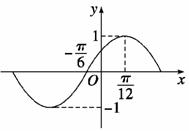
答案 y=cos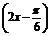
20.(16分)已知点M(x1,f(x1))是函数f(x)=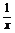 ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
(1)求切线l的方程;
(2)设l与x轴,y轴的交点分别为A、B,求△AOB周长的最小值.
解 (1)f′(x)=-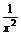 ,∴k=f′(x1)=-
,∴k=f′(x1)=-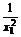 .
.
∴切线方程为y-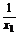 =-
=-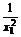 (x-x1),
(x-x1),
即y=-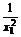 x+
x+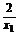 .
.
(2)在y=-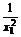 x+
x+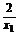 中,令y=0得x=2x1,
中,令y=0得x=2x1,
∴A(2x1,0).令x=0,得y=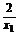 ,∴B
,∴B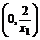 .
.
∴△AOB的周长m=2x1+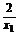 +
+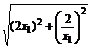 .
.
∴m=2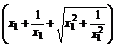 ,x1∈(0,+∞).
,x1∈(0,+∞).
令t=x1+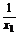 ,∵x1∈(0,+∞),∴t≥2.
,∵x1∈(0,+∞),∴t≥2.
∴当t=2,即x1=1时,m最小=2(2+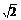 ).
).
故△AOB周长的最小值是4+2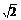 .
.
19.(16分)某厂家拟在2008年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用
m万元(m≥0)满足x=3-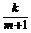 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2008年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2008年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2008年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2008年的促销费用投入多少万元时,厂家的利润最大.
解 (1)由题意可知当m=0时,x=1(万件),
∴1=3-k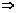 k=2.∴x=3-
k=2.∴x=3-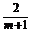 .
.
每件产品的销售价格为1.5×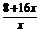 (元),
(元),
∴2008年的利润y=x·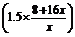 -(8+16x+m)
-(8+16x+m)
=4+8x-m=4+8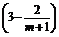 -m
-m
=-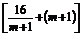 +29(m≥0).
+29(m≥0).
(2)∵m≥0时,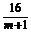 +(m+1)≥2
+(m+1)≥2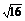 =8,
=8,
∴y≤-8+29=21,当且仅当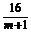 =m+1
=m+1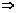 m=3(万元)时,ymax=21(万元).
m=3(万元)时,ymax=21(万元).
18.(16分)设f(x)是定义域为(-∞,0)∪(0,+∞)上的奇函数且在(-∞,0)上为增函数.
(1)若m·n<0,m+n≤0,求证:f(m)+f(n)≤0;
(2)若f(1)=0,解关于x的不等式f(x2-2x-2)>0.
(1)证明 ∵m·n<0,m+n≤0,∴m、n一正一负.
不妨设m>0,n<0,则n≤-m<0.取n=-m<0,
∵函数f(x)在(-∞,0)上为增函数,
则f(n)=f(-m);取n<-m<0,同理
f(n)<f(-m)∴f(n)≤f(-m).
又函数f(x)在(-∞,0)∪(0,+∞)上为奇函数,
∴f(-m)=-f(m).∴f(n)+f(m)≤0.
(2)解 ∵f(1)=0,f(x)在(-∞,0)∪(0,+∞)上为奇函数,∴f(-1)=0,
∴原不等式可化为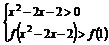 或
或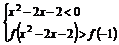 .
.
易证:f(x)在(0,+∞)上为增函数.
∴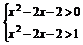 或
或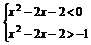 .
.
∴x2-2x-3>0或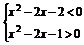 .
.
解得x>3或x<-1或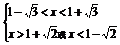 .
.
∴不等式的解集为
(-∞,-1)∪(1-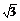 ,1-
,1-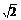 )∪(1+
)∪(1+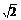 ,1+
,1+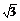 )∪(3,+∞).
)∪(3,+∞).
17.(14分)函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)不等式f(x)>ax-5当0<x<2时恒成立,求a的取值范围.
解 (1)令x=1,y=0,
得f(1+0)-f(0)=(1+2×0+1)·1=2,
∴f(0)=f(1)-2=-2.
(2)令y=0,f(x+0)-f(0)=(x+2×0+1)·x=x2+x,
∴f(x)=x2+x-2.
(3)f(x)>ax-5化为x2+x-2>ax-5,
ax<x2+x+3,∵x∈(0,2),
∴a<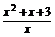 =1+x+
=1+x+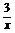 .
.
当x∈(0,2)时,1+x+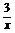 ≥1+2
≥1+2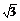 ,当且仅当x=
,当且仅当x=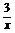 ,即x=
,即x=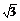 时取等号,由
时取等号,由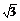 ∈(0,2),得
∈(0,2),得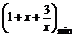 =1+2
=1+2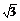 .
.
∴a<1+2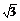 .
.
16.(2008·苏南四市模拟)(14分)甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x),g(x)以及任意的x≥0,当甲公司投入x万元做宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元做宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司这一新产品的开发有失败的风险,否则没有失败的风险.
(1)试解释f(0)=10,g(0)=20的实际意义;
(2)设f(x)= 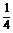 x+10,g(x)=
x+10,g(x)=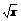 +20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
解 (1)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败的风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费.
(2)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
|
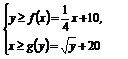 时,
时,
双方均无失败的风险.
由①②得y≥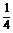 (
(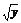 +20)+10,即4y-
+20)+10,即4y-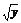 -60≥0,
-60≥0,
即(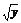 -4)(4
-4)(4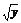 +15)≥0.
+15)≥0.
∵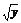 ≥0,∴4
≥0,∴4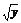 +15>0.
+15>0.
∴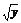 ≥4.∴y≥16.∴x≥
≥4.∴y≥16.∴x≥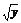 +20≥4+20=24.
+20≥4+20=24.
∴xmin=24,ymin=16,
即在双方均无失败风险的情况下,甲公司至少要投入24万元,乙公司至少要投入16万元.
15.(2008·石家庄模拟)(14分)已知a=(1,x),b=(x2+x,-x),m为常数且m≤-2,求使不等式a·b+2>m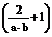 成立
成立
的x的范围.
解 ∵a=(1,x),b=(x2+x,-x),
∴a·b=x2+x-x2=x.
由a·b+2>m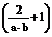
?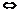 x+2>m
x+2>m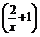
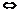 (x+2)-m
(x+2)-m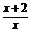 >0
>0
?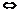 x(x+2)(x-m)>0(m≤-2).
x(x+2)(x-m)>0(m≤-2).
①当m=-2时,原不等式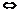 x(x+2)2>0
x(x+2)2>0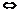 x>0;
x>0;
②当m<-2时,原不等式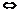 m<x<-2或x>0.
m<x<-2或x>0.
综上,得m=-2时,x的取值范围是(0,+∞);
m<-2时,x的取值范围是(m,-2)∪(0,+∞).
14.对于0≤m≤4的m,不等式x2+mx>4x+m-3恒成立,则x的取值范围是 .
答案 x<-1或x>3
解析 ∵x2-4x+3+m(x-1)>0,
即(x-1)(x-3+m)>0对0≤m≤4恒成立,
∴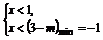 或
或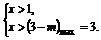
∴x<-1或x>3.
13.已知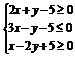 ,则(x+1)2+(y+1)2的最小值和最大值分别是
.
,则(x+1)2+(y+1)2的最小值和最大值分别是
.
答案 13,41
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com