
7.探究 特征
①熟悉公式的结构和特点;
②此公式对任意a、b都适用
③公式记号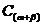
6.探究 由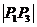 =
=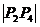 导出公式
导出公式
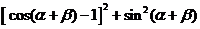

展开并整理得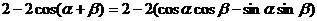
所以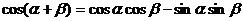 可记为
可记为 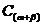
5.计算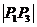 ,
,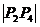
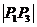 =
=
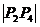 =
=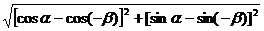
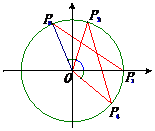
4.探究:写出4个点的坐标
 ,
,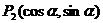
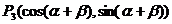 ,
,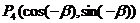 ,
,
3.探究:作单位圆,构造全等三角形
2.探究:在坐标系中a、b角构造a+b角
1.探究
反例: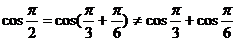
问题: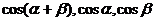 的关系?
的关系?
 解决思路:探讨三角函数问题的最基本的工具是直角坐标系中的单位圆及单位圆中的三角函数线
解决思路:探讨三角函数问题的最基本的工具是直角坐标系中的单位圆及单位圆中的三角函数线
3.练习:已知A(-1,5),B(4,-7) 求AB
解:
2.平面内任意两点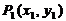 ,
,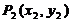 间的距离公式
间的距离公式
从点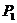 ,
,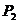 分别作x轴的垂线
分别作x轴的垂线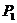
 ,
, 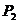
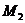 与x轴交于点
与x轴交于点 (
(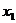 ,0),
,0), 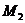 (
( ,0) 再从点
,0) 再从点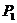 ,
,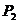 分别作y轴的垂线
分别作y轴的垂线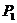
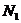 ,
, 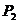
 与y轴交于点
与y轴交于点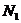 ,
,  直线
直线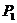
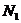 ,
, 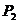
 与相交于Q点则:
与相交于Q点则: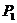 Q=
Q=
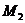 =|
=| -
-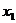 |
|
Q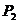 =
= 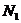
 =|
=|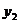 -
-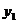 |
|
由勾股定理:
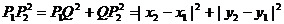
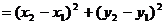
从而得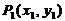 ,
,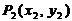 两点间的距离公式:
两点间的距离公式:
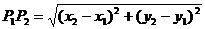
平面上的两点间距离公式
1.数轴上两点间的距离公式 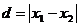
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com