
1.要在本章的教学中,应该根据教学实际,启发学生不断提出问题,研究问题。在对于正弦定理和余弦定理的证明的探究过程中,应该因势利导,根据具体教学过程中学生思考问题的方向来启发学生得到自己对于定理的证明。如对于正弦定理,可以启发得到有应用向量方法的证明,对于余弦定理则可以启发得到三角方法和解析的方法。在应用两个定理解决有关的解三角形和测量问题的过程中,一个问题也常常有多种不同的解决方案,应该鼓励学生提出自己的解决办法,并对于不同的方法进行必要的分析和比较。对于一些常见的测量问题甚至可以鼓励学生设计应用的程序,得到在实际中可以直接应用的算法。
1.3实习作业(约1课时)
1.2应用举例(约4课时)
1.1正弦定理和余弦定理(约3课时)
3.重视加强意识和数学实践能力
学数学的最终目的是应用数学,而如今比较突出的两个问题是,学生应用数学的意识不强,创造能力较弱。学生往往不能把实际问题抽象成数学问题,不能把所学的数学知识应用到实际问题中去,对所学数学知识的实际背景了解不多,虽然学生机械地模仿一些常见数学问题解法的能力较强,但当面临一种新的问题时却办法不多,对于诸如观察、分析、归纳、类比、抽象、概括、猜想等发现问题、解决问题的科学思维方法了解不够。针对这些实际情况,本章重视从实际问题出发,引入数学课题,最后把数学知识应用于实际问题。
1.数学思想方法的重要性
数学思想方法的教学是中学数学教学中的重要组成部分,有利于学生加深数学知识的理解和掌握。
本章重视与内容密切相关的数学思想方法的教学,并且在提出问题、思考解决问题的策略等方面对学生进行具体示范、引导。本章的两个主要数学结论是正弦定理和余弦定理,它们都是关于三角形的边角关系的结论。在初中,学生已经学习了相关边角关系的定性的知识,就是“在任意三角形中有大边对大角,小边对小角”,“如果已知两个三角形的两条对应边及其所夹的角相等,那么这两个三角形全”等。
教科书在引入正弦定理内容时,让学生从已有的几何知识出发,提出探究性问题:“在任意三角形中有大边对大角,小边对小角的边角关系.我们是否能得到这个边、角的关系准确量化的表示呢?”,在引入余弦定理内容时,提出探究性问题“如果已知三角形的两条边及其所夹的角,根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形.我们仍然从量化的角度来研究这个问题,也就是研究如何从已知的两边和它们的夹角计算出三角形的另一边和两个角的问题。”设置这些问题,都是为了加强数学思想方法的教学。
本章的中心内容是如何解三角形,正弦定理和余弦定理是解三角形的工具,最后落实在解三角形的应用上。通过本章学习,学生应当达到以下学习目标:
(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
(2)能够熟练运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的生活实际问题。
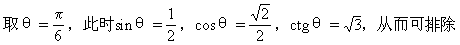
B、C、D,应选A.
[说明] 此例题用多种方法求解选项,指出3种选择题的技巧.
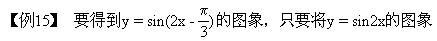
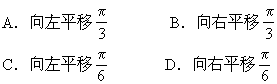
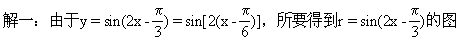
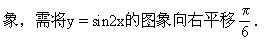
∴应选D
x轴交点中在原点右边最接近原点的交点,而在原点左边与x轴交点中最

的图象.
∴选D
[说明] y=Asin(ωx+j)(A>0,ω>0)x∈R的图象可由y=sinx的图象经下列各种顺序变换得到的.
(1)先平移,后伸缩:
①把y=sinx的图象向左(j>0)或向右(j<0)沿x轴方向平移|j|个单位;(相位变换)

(周期变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍,横坐标不变(振幅变换)
(2)先伸缩,后平移
①把y=sinx图象上各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原

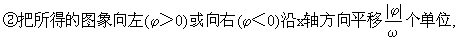
(相位变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍横坐标不变(振幅变换)
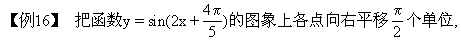
再把横坐标缩小到原来的一半,纵坐标扩大到原来的4倍,则所得的图象的解析式是 [ ]


∴选A.
[例17] 方程sin2x=sinx在区间(0,2π)内解的个数是
[ ]
A.1 B.2 C.3 D.4
[分析] 本题有两类解法
(1)求出方程在(0,2π)内的所有解,再数其解的个数.而决定选项,对于选择题,此法一般不用.
(2)在同一坐标系中作出函数y=sin2x和y=sinx的图象,如图2-18所示.
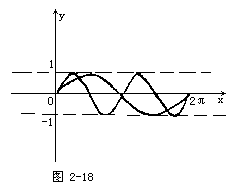
它们在(0,2π)内交点个数,即为所求方程解的个数,从而应选C.

它体现了数、形的结合.
[例18] 设函数f(x)是定义在R上的周期为3的奇函数,且f(1)=2,则f(5)=____
解:∵f(x)是奇函数,且f(1)=2,∴f(-1)=-2
又∵f(x)是周期为3的函数. ∴f(3+x)=f(x)
∴f(-1+3)=f(-1)=-2 即f(2)=-2
f(2+3)=f(2)=-2 即f(5)=-2
[例19] 有一块扇形铁板,半径为R,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都在扇形的半径或弧上,求这个内接矩形的最大面积.
[分析] 本题入手要解决好两个问题.
(1)内接矩形的放置有两种情况,如图2-19所示,应该分别予以处理.
(2)求最大值问题这里应构造函数,怎么选择便于以此表达矩形面积的自变量.
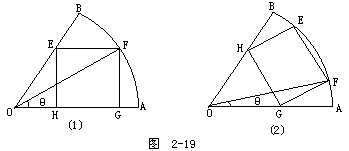
解:如图2-19(1)设∠FOA=θ,则FG=Rsinθ
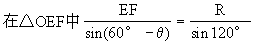
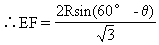
又设矩形EFGH的面积为S,那么
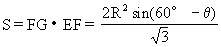
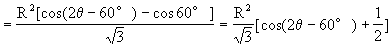
又∵0°<θ<60°,故当cos(2θ-60°)=1,即θ=30′时,
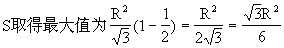
如图2-19 (2),设∠FOA=θ,则EF=2Rsin(30°-θ),在△OFG中,∠OGF=150°
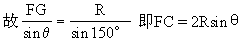
设矩形的面积为S.
那么S=EFFG=4R2sinθsin(30°-θ)
=2R2[cos(2θ-30°)-cos30°]
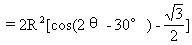
又∵0<θ<30°,故当cos(2θ-30°)=1

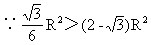

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com