
6.给出下列关于互不相同的直线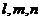 和平面
和平面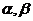 的四个命题:
的四个命题:
①若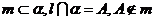 ,则
,则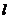 与
与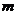 不共面;
不共面;
②若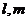 是异面直线,
是异面直线,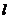 ∥
∥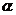 ,
,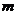 ∥
∥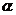 且
且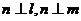 ,则
,则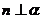 ;
;
③若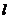 ∥
∥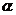 ,
,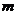 ∥
∥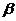 ,
,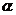 ∥
∥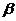 ,且
,且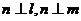 ,则
,则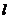 ∥
∥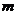 ;
;
④若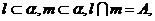
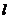 ∥
∥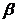 ,
,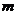 ∥
∥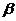 则
则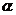 ∥
∥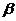
 ;
;
其中为假命题的是 
A.①
B.②
C.③ D.④
5.函数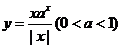 的图象的大致形状是
的图象的大致形状是
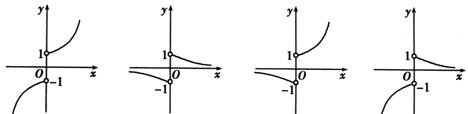
A. B. C. D.
4. 已知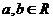 ,那么“
,那么“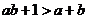 ”是“
”是“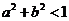 ”的
”的
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
3. 在等差数列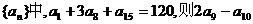 =
=
A.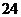 B.
B.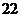 C.
C.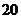 D.
D.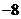
2.
已知一直线倾斜角的余弦值是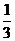 ,则此直线的斜率是
,则此直线的斜率是
A.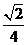 B.
B.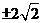 C.
C.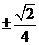 D.
D. 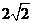
1.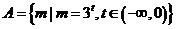 ,
,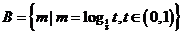 ,则
,则
A.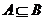 B.
B.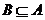 C.
C.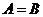 D.
D.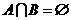
22. (本小题满分14分)
解:(Ⅰ)设圆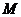 的方程为:
的方程为: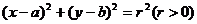 …………………………1分
…………………………1分
根据题意得: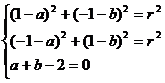 …………………………4分
…………………………4分
解得;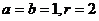
故所求圆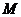 的方程为:
的方程为: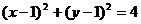 …………………………6分
…………………………6分
(Ⅱ)因为四边形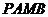 面积
面积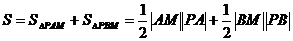 ………8分
………8分
又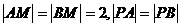
所以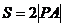 ,而
,而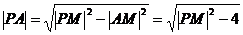
即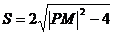 …………………………10分
…………………………10分
因此要求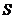 的最小值,只需求
的最小值,只需求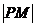 的最小值即可
的最小值即可
即在直线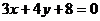 上找一点
上找一点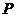 ,使得
,使得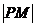 的值最小…………………………12分
的值最小…………………………12分
所以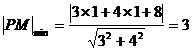
所以四边形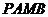 面积的最小值为
面积的最小值为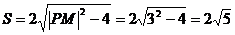 ………14分
………14分
21.解:(Ⅰ)设切点坐标为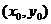 ,由
,由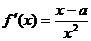 得:………………………2分
得:………………………2分
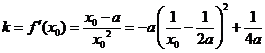 …………………………4分
…………………………4分
根据题意知: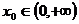 ,即
,即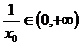 ,所以
,所以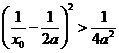
又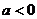 ,则
,则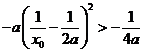 ,即
,即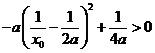
所以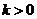 …………………………6分
…………………………6分
(Ⅱ)显然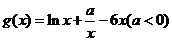 的定义域为
的定义域为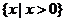 …………………………7分
…………………………7分
根据(Ⅰ)与题意知: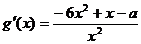 …………………………8分
…………………………8分
又因为函数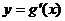 的图象经过点
的图象经过点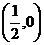 ,代入
,代入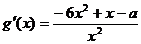 求得:
求得: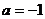
则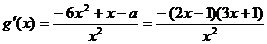 …………………………10分
…………………………10分
由此可知:当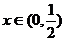 时,有
时,有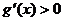 ,此时
,此时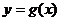 为单调增函数;
为单调增函数;
当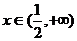 时,有
时,有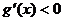 ,此时
,此时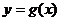 为单调减函数;
为单调减函数;
所以函数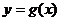 在区间
在区间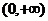 上只有极大值,
上只有极大值,
即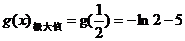 .…………………………12分
.…………………………12分
20.解:(Ⅰ)由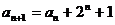 变形得:
变形得: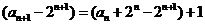
即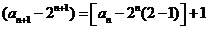 所以
所以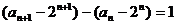 ……4分
……4分
故数列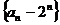 是以
是以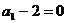 为首项,
为首项,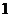 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(Ⅱ)由(Ⅰ)得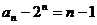 …………………………6分
…………………………6分
所以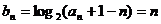 …………………………7分
…………………………7分
设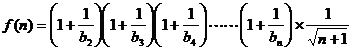 ………………8分
………………8分
则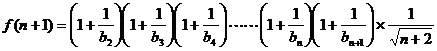
两式相除得: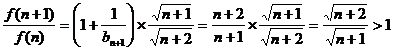 ……10分
……10分
所以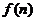 是关于
是关于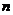 的单调递增函数,则
的单调递增函数,则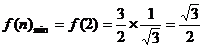
故实数 的取值范围是
的取值范围是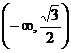 …………………………12分
…………………………12分
19.(本小题满分12分)
解:(Ⅰ)证明:因为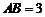 ,
, ,
,
所以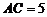 ,从而
,从而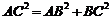 ,即
,即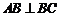 .………………………3分
.………………………3分
又因为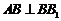 ,而
,而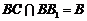 ,
,
所以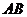
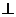 平面
平面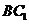
又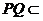 平面
平面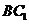
所以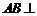
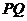 ;………………5分
;………………5分
(Ⅱ)解:假设存在一点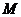 满足
满足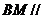 平面
平面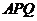 ,过
,过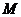 作
作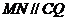 交
交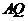 于
于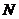
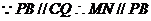 …………………………8分
…………………………8分
连接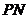 ,因为
,因为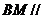 平面
平面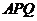
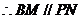
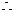 四边形
四边形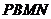 为平行四边形…………………………10分
为平行四边形…………………………10分
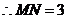 ,
,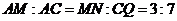
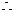 当点
当点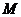 满足
满足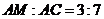 时,
时, 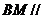 平面
平面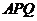 .…………………………12分
.…………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com