
8.已知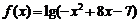 在
在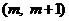 上是增函数,则
上是增函数,则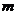 的取值范围是 .
的取值范围是 .
7.设函数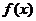 是定义在R上以3为周期的奇函数,若
是定义在R上以3为周期的奇函数,若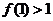 ,
, ,则a的取值范围是__________________________.
,则a的取值范围是__________________________.
6.函数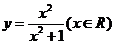 的值域为________________.
的值域为________________.
5.设M={a,b},则满足M∪N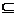 {a,b,c}的非空集合N的个数为______________.
{a,b,c}的非空集合N的个数为______________.
4.集合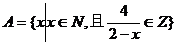 用列举法可表示为A=_____________.
用列举法可表示为A=_____________.
3.函数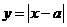 的图象关于直线
的图象关于直线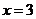 对称.则
对称.则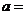 _____________.
_____________.
2.已知函数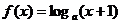 的定义域和值域都是
的定义域和值域都是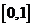 ,则实数a的值是
________
,则实数a的值是
________
1.函数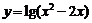 的定义域是____________________.
的定义域是____________________.
补充:⑴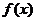 =
= 是以(
是以(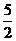 ,
, )为顶点、对称轴平行于y轴、开口向上的抛物线(如图);它的单调区间是(-
)为顶点、对称轴平行于y轴、开口向上的抛物线(如图);它的单调区间是(-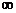 ,
,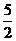 ]与[
]与[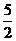 ,+
,+ 
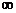 );它在(-
);它在(-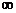 ,
,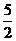 ]上是减函数,在[
]上是减函数,在[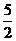 ,+
,+ 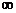 )上是增函数.
)上是增函数.
证明:设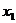 <
<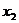
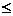
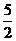 ,则
,则
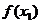 -
-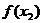 =
=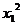 -
-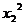 -5(
-5(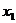 -
-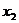 )
)
 =(
=(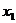 +
+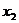 -5) (
-5) (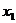 -
-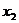 )
)
∵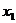 <
<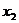
 ,∴
,∴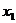 +
+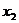 <5,
<5,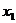 -
-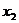 <0,
<0,
∴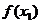 -
-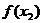 >0,即
>0,即 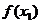 >
> 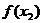 ..
..
∴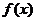 =
=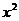 -5
-5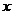 +6在(-
+6在(-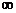 ,
,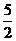 ]上是减函数.
]上是减函数.
类似地,可以证明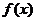 在[
在[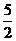 ,+
,+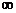 )上是增函数.
)上是增函数.
⑵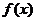 =-
=-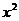 +9的图象是以(0,9)为顶点、
+9的图象是以(0,9)为顶点、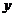 轴为对称轴、开口向下的一条抛物线(如图);它的单调区间是(-
轴为对称轴、开口向下的一条抛物线(如图);它的单调区间是(-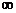 ,0]与[0,+
,0]与[0,+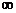 ),它在(-
),它在(-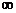 ,0]上是增函数,在[0,+
,0]上是增函数,在[0,+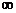 )上是减函数.
)上是减函数.
证明:设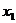 <
<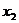
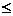 0,则
0,则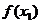 -
-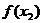 =-
=-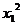 +
+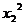 =(
=(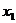 +
+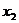 ) (
) (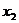 -
-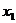 )
)
∵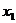 <
<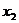
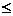 0,∴
0,∴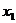 +
+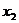 <0,
<0,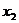 -
-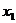 >0,
>0,
∴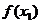 -
-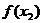 <0,即
<0,即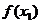 <
<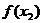
.∴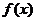 =9-
=9-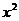 在(-
在(-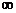 ,0]上是增函数.
,0]上是增函数.
类似地,可以证明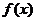 在[0,+
在[0,+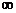 )上是减函数.
)上是减函数.
⒉根据定义证明函数单调性的一般步骤是:⑴设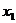 ,
,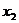 是给定区间内的任意两个值,且
是给定区间内的任意两个值,且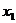 <
<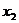 ;⑵作差
;⑵作差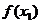 -
-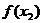 ,并将此差式变形(要注意变形的程度);⑶判断
,并将此差式变形(要注意变形的程度);⑶判断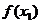 -
-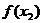 的正负(要注意说理的充分性);⑷根据
的正负(要注意说理的充分性);⑷根据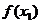 -
-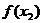 的符号确定其增减性.
的符号确定其增减性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com