
4. 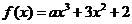 ,若
,若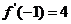 ,则
,则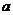 的值等于( )
的值等于( )
A. 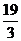 B.
B. 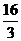 C.
C.  D.
D. 

3. 函数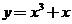 的递增区间是( )
的递增区间是( )
A. 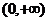 B.
B. 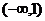 C.
C. 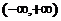 D.
D. 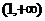

2. 一个物体的运动方程为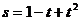 其中
其中 的单位是米,
的单位是米,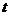 的单位是秒,那么物体在
的单位是秒,那么物体在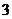 秒末的瞬时速度是( )
秒末的瞬时速度是( )
A. 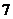 米/秒 B.
米/秒 B. 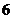 米/秒 C.
米/秒 C. 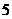 米/秒 D.
米/秒 D.  米/秒
米/秒
1. 若函数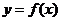 在区间
在区间 内可导,且
内可导,且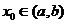 则
则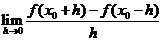 的值为( )
的值为( )
A.  B.
B. 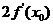 C.
C.  D.
D. 

28.(09·丰台模拟)如图所示,宽度为L=0.20 m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=1.0Ω的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B=0.50 T。一根质量为m=10g的导体棒MN放在导轨上与导轨接触良好,导轨和导体棒的电阻均可忽略不计。现用一平行于导轨的拉力拉动导体棒沿导轨向右匀速运动,运动速度v=10 m/s,在运动过程中保持导体棒与导轨垂直。求:
(1)在闭合回路中产生的感应电流的大小;
(2)作用在导体棒上的拉力的大小;
(3)当导体棒移动30cm时撤去拉力,求整个过程直到MN静止时电阻R上产生的热量。
答案:(1)感应电动势为 E=BLv=1.0V
感应电流为 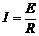 =1.0 A
=1.0 A
(2)导体棒匀速运动,安培力与拉力平衡
即有F=BIL=0.1N
(3) 导体棒移动30cm的时间为 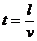 = 0.03s
= 0.03s
根据焦耳定律,Q1 = I2R t = 0.03J (或Q1=Fs=0.03J)
根据能量守恒,Q2=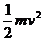 =
0.5
=
0.5
电阻R上产生的热量 Q = Q1+Q2 = 0.53J
27.(09·石景山模拟)如图(甲)所示,边长为L=2.5m、质量m=0.50kg的正方形绝缘金属线框,平放在光滑的水平桌面上,磁感应强度B=0.80T的匀强磁场方向竖直向上,金属线框的一边ab与磁场的边界MN重合.在力F作用下金属线框由静止开始向左运动,在5.0s内从磁场中拉出.测得金属线框中的电流随时间变化的图象如图(乙)所示.已知金属线框的总电阻为R=4.0Ω.
(1)试判断金属线框从磁场中拉出的过程中,线框中的感
应电流方向?
(2)t=2.0s时,金属线框的速度?
(3)已知在5.0s内力F做功1.92J,那么,金属框从磁场拉出过程线框中产生的焦耳热是多少?
答案:(1)由楞次定律(或右手定则),线框中感应电流的方向为逆时针(或abcda)
(2)设t=2.0s时的速度为v,据题意有:BLv=IR 解得 m/s=0.4m/s
m/s=0.4m/s
(3)设t=5.0s时的速度为v′,整个过程中线框中产生的焦耳热为Q,则有:
BLv′=I′R
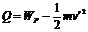
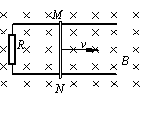 由上述两式解得:
由上述两式解得: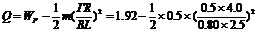 J=1.67J
J=1.67J
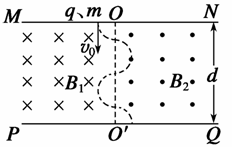
26.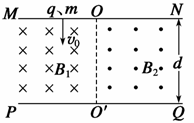 (郴州市2009届高三调研试题)如图所示,在直线MN与PQ之间有两个匀强磁场区域,两磁场的磁感应强度分别为Bl、B2,方向均与纸面垂直,两磁场的分界线
(郴州市2009届高三调研试题)如图所示,在直线MN与PQ之间有两个匀强磁场区域,两磁场的磁感应强度分别为Bl、B2,方向均与纸面垂直,两磁场的分界线 和PQ都垂直.现有一带正电的粒子质量为m、电荷量为q,以速度
和PQ都垂直.现有一带正电的粒子质量为m、电荷量为q,以速度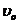 垂直边界MN射入磁场B1,并最终垂直于边界PQ从
垂直边界MN射入磁场B1,并最终垂直于边界PQ从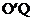 段射出,已知粒子始终在纸面内运动,且每次均垂直
段射出,已知粒子始终在纸面内运动,且每次均垂直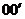 越过磁场分界线.
越过磁场分界线.
(1)写出MN与PQ间的距离d的表达式。
(2)用d、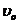 表示粒子在磁场中运动的时间。
表示粒子在磁场中运动的时间。
解:(1)粒子在
 Q间射出,轨迹如图所示。
Q间射出,轨迹如图所示。
 由 qv0B=mv02/R1
由 qv0B=mv02/R1
得R1=mv02/qB1
同理得 R2=mv02/qB2
又d=(2n+1)(R1+R2)
(n=0,1,2,3……)
因此d=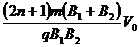 。
。
(2)粒子在磁场B1中做圆周运动的周期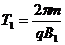 ,在磁场B2中做圆周运动的周期
,在磁场B2中做圆周运动的周期 
粒子在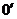 Q间射出,在两个磁场中分别经历2n+1个
Q间射出,在两个磁场中分别经历2n+1个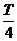 ,所以
,所以

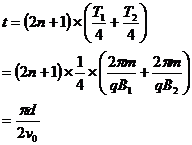
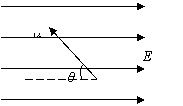
25.(郴州市2009届高三调研试题)如图所示,一质量为m、电量为+q的带电小球以与水平方向成某一角度θ的
初速度v0射入水平方向的匀强电场中,小球恰能在电场中做直线运动.若电场的场强
 大小不变,方向改为相反同时加一垂直纸面向外的匀强磁场,小球仍以原来的初速
大小不变,方向改为相反同时加一垂直纸面向外的匀强磁场,小球仍以原来的初速
度重新射人,小球恰好又能做直线运动.求电场强度的大小、磁感应强度的大小和
初速度与水平方向的夹角θ。
解:在没有磁场,只有电场时,设小球的运动方向与水平方向的夹角为θ受力情况
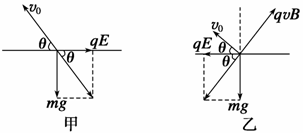 如图甲所示.
如图甲所示.
根据已知得:
在既有磁场又有电场时,E不变,受力情况如图乙,由几何知识得θ=450
小球仍做直线运动,有: 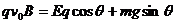
解得:B= 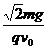
E=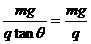
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com