
例6. 求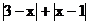 的最小值。
的最小值。

解:如图2,设数轴上的三点A、B、C所表示的数分别为1、3、x,其中C可视为一个动点,这样,此题就可转化为求 的最小值。由图形可知,当点C在线段AB上时
的最小值。由图形可知,当点C在线段AB上时 最小,此时
最小,此时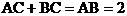 ,故当
,故当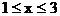 时,
时,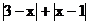 有最小值,其最小值为2。
有最小值,其最小值为2。
例5. 求代数式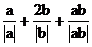 的值。
的值。
解:(1)当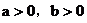 时,
时,
原式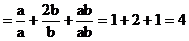
(2)当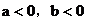 时,
时,
原式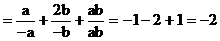
(3)当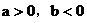 时,
时,
原式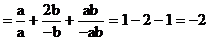
(4)当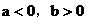 时,
时,
原式
综上所述,所求代数式的值为4、 和0。
和0。
例4. 如果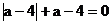 ,那么a的取值范围是_________。
,那么a的取值范围是_________。
解:由已知式可知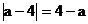
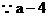 与
与 互为相反数
互为相反数
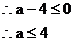
注意:在这里许多同学只重视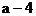 是一个负数,而忽视了
是一个负数,而忽视了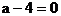 也成立这一特殊性,易把答案填为
也成立这一特殊性,易把答案填为 。
。
例3. 已知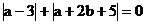 ,求
,求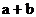 的值。
的值。
解: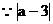 与
与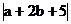 都是非负数,且它们的和为零
都是非负数,且它们的和为零
 且
且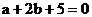
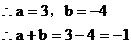
例2. 已知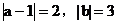 ,且
,且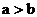 ,则
,则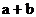 的值为_________。
的值为_________。
解: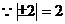
 或
或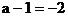
 或
或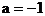
同理可得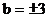
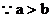
 或
或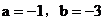
故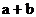 的值为0或
的值为0或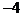
例1. 三个数a、b、c在数轴上的对应点如图1,化简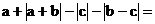 _____。
_____。
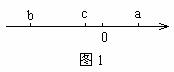
解:由图1可知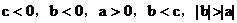 。
。
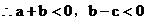
∴原式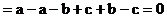
例5. 如图5所示,在锐角△ABC中,高线BE与CF相交于H,
求证: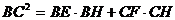 。
。
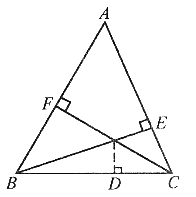
图5
分析:求证式中的右端有线段的积,这使我们联想到如能创造出相似三角形,则会有对应线段成比例,就会出现线段的乘积式,为此添辅助线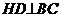 于D,则出现相似三角形,而求证式中的右端均为相似三角形的边,故可从相似三角形开始证明。
于D,则出现相似三角形,而求证式中的右端均为相似三角形的边,故可从相似三角形开始证明。
证明:过H作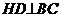 交BC于D。
交BC于D。
则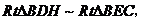
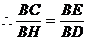
即 (1)
(1)
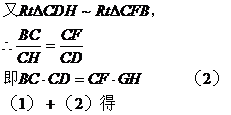

例4. 如图4所示,已知O是△ABC内的一点,过O作EF、QP、GH分别平行于BC、CA、AB。
求证: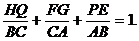
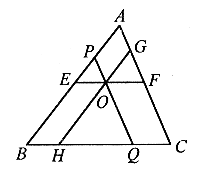
图4
分析:求证的是三个比的和为1,只要求得与这三个比的分母是同一条线段,并且分子线段的和等于分母线段即可。
证明:在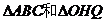 中,
中,
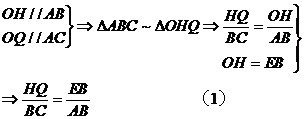
在△ABC和△GOF中,
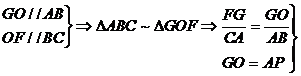

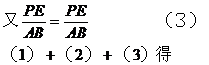
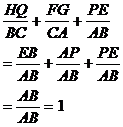
例3. 如图3所示,已知一直线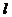 截△ABC的边AB,AC和BC的延长线于F、E、D。
截△ABC的边AB,AC和BC的延长线于F、E、D。
求证: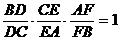

图3
证明:过点C作CG//FD,交AB于G。
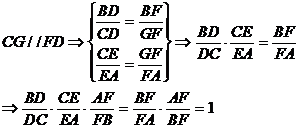
例1. 如图1所示,在△ABC中,∠A的平分线交BC于P,∠A的外角平分线交BC延长线于Q,O是PQ之中点。

图1
求证: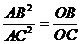
证明:因为AP平分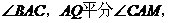
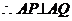
又因为O是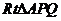 斜边PQ之中点,连AO,得OA=OP。因为
斜边PQ之中点,连AO,得OA=OP。因为
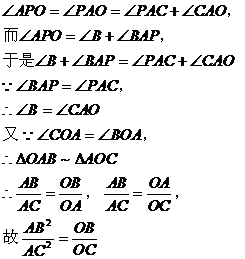
例2. 如图2所示,已知△ABC中,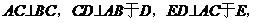 DF⊥BC于F。
DF⊥BC于F。
求证: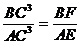
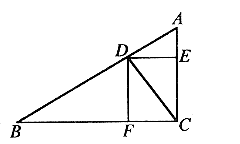
图2
证明: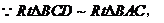
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com