例2. 已知一次函数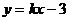的图像过点(2，－1)，求这个函数的解析式。

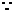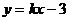　　 解：一次函数的图像过点(2，－1)

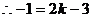　　 ，即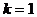

　　 故这个一次函数的解析式为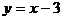

　　 变式问法：已知一次函数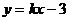，当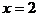时，y＝－1，求这个函数的解析式。

　　 例1. 已知函数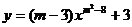是一次函数，求其解析式。

　　 解：由一次函数定义知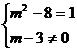

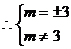
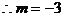　　 ，故一次函数的解析式为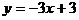

　　 注意：利用定义求一次函数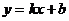解析式时，要保证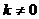。如本例中应保证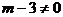

解:过P作内公切线交AB于E,由切线长定理知EB=EP,EP=EA,即EB=EP=EA,根据定理(在一个三角形中,一边上的中线等于该边的一半,那么这个三角形是直角三角形)知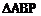为直角三角形.

此题中AB为外公切线与两圆的切点,P为两圆切点.

我们习惯上把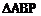称为切点三角形.

在关于两圆外切关系的几何证明题中,运用切点三角形来分析问题,解决问题,可以收到事半功倍的效果,它的应用在两圆外切中尤为重要.

性质(4) 切点三角形是直角三角形.

例4(重庆市中考题)如图4, ⊙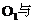⊙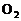外切于点P,内公切线PC与外公切线AB(A、B分别是⊙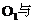⊙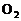上的切点)相交于点C,已知⊙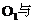⊙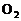的半径分别为3、4,则PC的长等于________.

分析:由于AB为外公切线,由性质(2)知

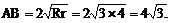
又由性质(4)知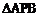为直角在三角形且CP=CB=AC,故CP为斜边AB上的中线,因此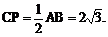

例5.如图5, ⊙⊙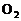外切于点P,AB为两圆的外公切线,切点为A、B,连心线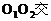

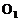⊙于C,交⊙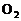于D,CA与DB的延长线相交于Q,求证:.

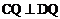简析：连AP、BP,由上题知∠APB=Rt∠,又∠CAP=∠PBD=Rt∠,故由四边形内角和定理知∠Q=Rt∠,即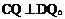

两圆外切关系的这些性质,在解题时要灵活的应用.在例4、例5中的切点三角形并不是现成有的,而是添线构造出来的,难度稍大些,因此脑子中对切点三角形这些性质必须有深刻的印象,才能举一反三,触类旁通.

如图1，半径为r、R的⊙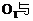⊙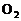外切，外公切线AB分别切⊙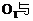⊙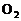于A、B，那么AB就是外公切线长。连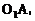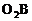，由切线性质知

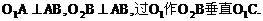可证得四边形ABCD为矩形，得

，

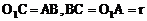因此，，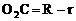

而在RtΔ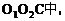

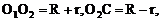
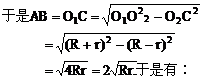
性质(2)　 外公切线长等于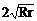

7　　　　 两圆外切,经常添的辅助线是内公切线,因为内公切线可以产生两圆相等的弦切角,可将两圆的元素联系起来.

性质(3)　 添内公切线是解决两圆外切问题的金钥匙.

例2　 已知如图2, ⊙⊙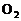外切于点C,PA切⊙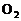于点A,交⊙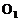于点P、D，直接PC交⊙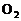于点B。

求证：AC平分∠BCD。

解：过C作⊙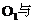⊙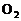的内公切线`MN交AP于M，所以∠MCD=∠P.

又PA切⊙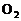于点A,

所以∠MAC=∠ACM,

所以∠ACB=∠P+∠MAC=∠MCD+∠MCA=∠DCA.

即AC平分∠BCD.

　　 如图所示，抛物线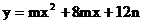与x轴交于A、B两点(点A在点B的左边)，在第二象限内抛物线上的一点C，使△OCA∽△OBC，且AC：BC=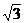：1，若直线AC交y轴于P。

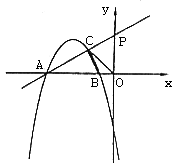
　　 (1)当C恰为AP中点时，求抛物线和直线AP的解析式；

　　 (2)若点M在抛物线的对称轴上，⊙M与直线PA和y轴都相切，求点M的坐标。

　　 如图所示，已知BC是半圆O的直径，△ABC内接于⊙O，以A为圆心，AB为半径作弧交⊙O于F，交BC于G，交OF于H，AD⊥BC于D，AD、BF交于E，CM切⊙O于C，交BF的延长线于M，若FH=6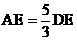，，求FM的长。

　　 已知关于x的方程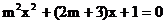　 ①的两实根的乘积等于1。

　　 (1)求证：关于x的方程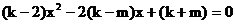　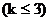 　方程②有实数根；

　　 (2)当方程②的两根的平方和等于两根积的2倍时，它的两个根恰为△ABC的两边长，若△ABC的三边都是整数，试判断它的形状。

2. 如图所示，⊙O中，弦AC、BD交于E，。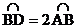

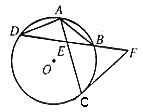
　　 (1)求证：；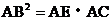

　　 (2)延长EB到F，使EF=CF，试判断CF与⊙O的位置关系，并说明理由。

1. 某水果批发市场规定，批发苹果不少于100千克，批发价为每千克2.5元，学校采购员带现金2000元，到该批发市场采购苹果，以批发价买进，如果采购的苹果为x(千克)，付款后剩余现金为y(元)。

　　 (1)写出y与x间的函数关系式，并写出自变量x的取值范围，画出函数图象；

　　 (2)若采购员至少留出500元去采购其他物品，则它最多能购买苹果多少千克？

2. 已知：如图所示，Rt△ABC中，∠C=90°，∠ABC=60°，DC=11，D点到AB的距离为2，求BD的长。