
1. 在 AOB的两边OA、OB上分别截取OM、ON,使OM=ON。
AOB的两边OA、OB上分别截取OM、ON,使OM=ON。
3. 作射线OC,OC就是 AOB的平分线。
AOB的平分线。
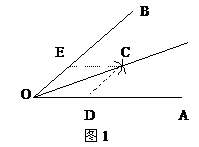
证明 连结EC、DC
因为OD=OE,DC=EC,OC=OC
所以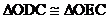
所以 COA=
COA= COB
COB
作法2 (课本第55页第3题)
如图2,在 AOB的两边OA、OB上分别取OM=ON,分别过点M、N作OA、OB的垂线,交点为P,画出射线OP。
AOB的两边OA、OB上分别取OM=ON,分别过点M、N作OA、OB的垂线,交点为P,画出射线OP。
证明 OP平分 AOB
AOB
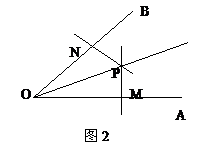
分析 该题的已知是尺规作图的另一种方法,可引导学生按照题意写出已知、求作、作法与证明。
作图步骤:
2. 分别以D、E为圆心,以大于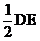 的长为半径作弧,两弧在
的长为半径作弧,两弧在 AOB内交于点C。
AOB内交于点C。
1. 如图1,在OA、OB上分别截取OD、OE,使OD=OE。
2. 多项式除以单项式
运算法则是:多项式除以单项式,就是用这个多项式的每一项分别除以单项式,再将所得的商相加。
例2 计算:
(1)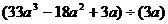
(2)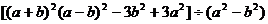
解:(1)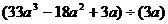
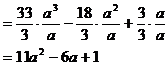
(2)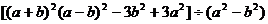
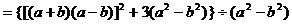
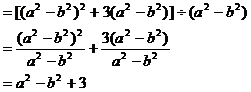
注:此题中,将被除式看作是以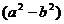 为字母的多项式。
为字母的多项式。
1. 单项式除以单项式
运算法则:将被除式,除式里的数字系数、同字母的幂分别相除,它们的积,作为商的因式,对只在被除式里含有的字母,则连同它的指数一起作为商的一个因式。
例1 计算:
(1)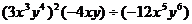
(2)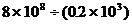
(3)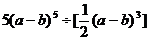
解:(1)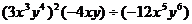
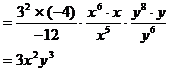
(2)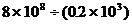
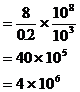
注:此题中,10被看作字母。
(3)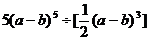
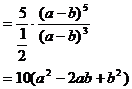
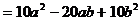
注:这里,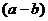 被看作一个字母。
被看作一个字母。
3. 算术平方根:任何一个非负数的算术平方根都是一个非负数,即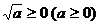 。
。
解题过程中巧用以上三个非负性质可以简捷地处理许多问题。现举例说明如下。
例1. 已知a、b为实数,且满足 ,求ab的值。
,求ab的值。
分析:解决本题只需从已知等式中求出a、b值即可。应用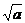 中
中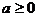 的非负性质可以立即求出b的值,从而进一步得到a的值。
的非负性质可以立即求出b的值,从而进一步得到a的值。
解:由题意可知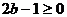 且
且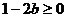
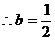 ,此时
,此时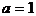
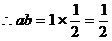
例2. 若a、b、c满足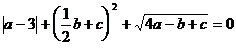 ,求
,求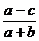 的值。
的值。
解:由非负数的性质可知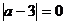 ,且
,且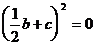 ,且
,且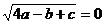
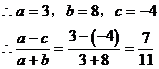
例3. 已知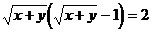 ,求
,求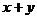 的值。
的值。
解:已知等式可化为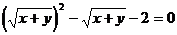
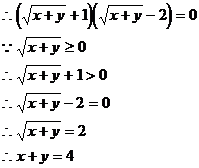
2. 平方:任何一个实数的平方都是非负数,即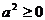 。
。
1. 绝对值:任何一个实数的绝对值都是非负数,即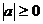 。
。
4. 反向延长射线构造平角
例4 如图4,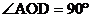 ,OD为
,OD为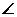 BOC的平分线,OE为BO的延长线。
BOC的平分线,OE为BO的延长线。
求证: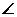 COE=2
COE=2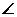 AOB。
AOB。
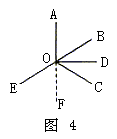
证明:反向延长射线AO得射线OF
因为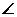 AOD为直角,
AOD为直角,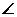 AOF为平角
AOF为平角

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com