
2.NA为阿伏加德罗常数,下列说法正确的是 ( )
A.标准状况下,22.4L苯中含有NA个苯分子
B.14g N2含有的核外电子总数为14NA
C.1 mol乙炔分子含3NA个碳碳叁键
D.23g金属钠与足量水反应时失去的电子数是NA
1.下列说法与“节能减排”不相符的是 ( )
A.推广氢能等新能源的使用,逐步替代化石燃料
B.将未经分类处理的垃圾集中填埋
C.有计划、有节制地开采煤、石油、天然气等矿物资源
D.倡导“绿色化学”理念,逐步实现化工企业零排放
1 求证:
求证:
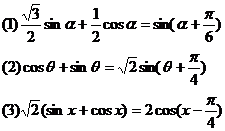
2 利用和(差)角公式化简:
利用和(差)角公式化简:
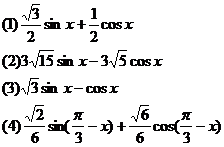
1 证明(1)
证明(1) 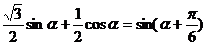
证法一:左边=sinαcos +cosαsin
+cosαsin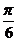 =sin(α+
=sin(α+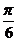 )=右边
)=右边
证法二:右边=sinαcos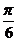 +cosαsin
+cosαsin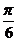 =
=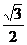 sinα+
sinα+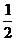 cosα=左边
cosα=左边
(2)cosθ+sinθ=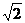 sin(θ+
sin(θ+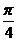 )
)
证法一:左边=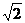 (
(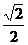 cosθ+
cosθ+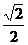 sinθ)
sinθ)
=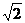 (sin
(sin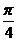 cosθ+cos
cosθ+cos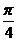 sinθ)
sinθ)
=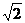 sin(θ+
sin(θ+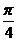 )=右边
)=右边
证法二:右边=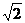 (sinθcos
(sinθcos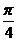 +cosθsin
+cosθsin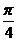 )
)
=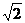 (
(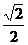 sinθ+
sinθ+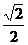 cosθ)
cosθ)
=cosθ+sinθ=左边
(3) 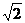 (sinx+cosx)=2cos (x-
(sinx+cosx)=2cos (x-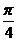 )
)
证法一:左边=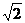 (sinx+cosx)=2(
(sinx+cosx)=2(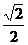 sinx+
sinx+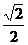 cosx)
cosx)
=2(cosxcos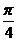 +sinxsin
+sinxsin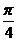 )
)
=2cos(x-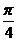 )=右边
)=右边
证法二:右边=2cos(x-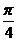 )=2(cosxcos
)=2(cosxcos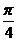 +sinxsin
+sinxsin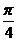 )
)
=2(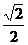 cosx+
cosx+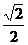 sinx)
sinx)
=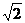 (cosx+sinx)=左边
(cosx+sinx)=左边
2 解:(1)
解:(1) 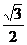 sinx+
sinx+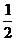 cosx=sinxcos
cosx=sinxcos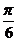 +cosxsin
+cosxsin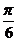 =sin(x+
=sin(x+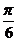 )
)
或:原式=sinxsin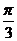 +cosxcos
+cosxcos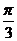 =cos(x-
=cos(x-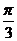 )
)
(2)3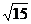 sinx-3
sinx-3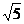 cosx=6
cosx=6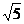 (
(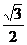 sinx-
sinx-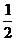 cosx)
cosx)
=6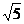 (sinxcos
(sinxcos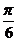 -cosxsin
-cosxsin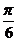 )
)
=6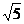 sin(x-
sin(x-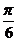 )
)
或:原式=6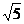 (sin
(sin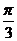 sinx-cos
sinx-cos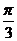 cosx)=-6
cosx)=-6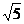 cos(x+
cos(x+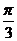 )
)
(3) 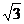 sinx-cosx=2(
sinx-cosx=2(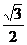 sinx-
sinx-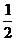 cosx)
cosx)
=2sin(x-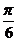 )=-2cos(x+
)=-2cos(x+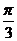 )
)
(4) 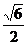 sin(
sin(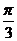 -x)+
-x)+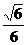 cos(
cos(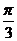 -x)
-x)
=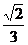 [
[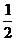 sin(
sin(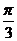 -x)+
-x)+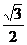 cos(
cos(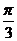 -x)]
-x)]
=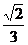 [sin
[sin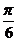 sin(
sin(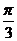 -x)+cos
-x)+cos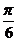 cos(
cos(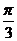 -x)]
-x)]
=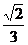 cos[
cos[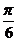 -(
-(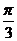 -x)]=
-x)]=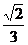 cos(x-
cos(x-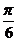 )
)
或:原式=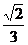 [sin(
[sin(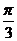 -x)cos
-x)cos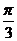 +cos(
+cos(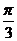 -x)sin
-x)sin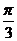 ]
]
=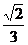 sin[(
sin[(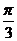 -x)+
-x)+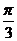 ]=
]=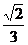 sin(
sin(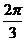 -x)
-x)
4°角变换 5°“升幂”与“降次” 6°辅助角
1 已知 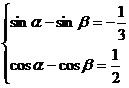

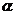 、
、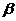 均为锐角,求
均为锐角,求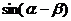 的值.
的值.
分析:由于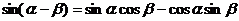 ,由已知两式一时得不到
,由已知两式一时得不到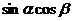 与
与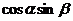 的值,而只能出现
的值,而只能出现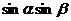 与
与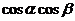 一类的值,例如
一类的值,例如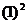 +
+ ,得
,得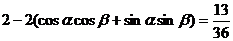 ,化简、整理得
,化简、整理得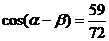 .由此要求
.由此要求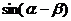 的值,固然有路可循,但是还要进一步定出
的值,固然有路可循,但是还要进一步定出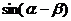 的值的符号才行.
的值的符号才行.
2 已知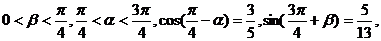 求
求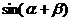 的值.
的值.
提示: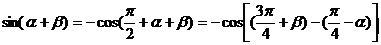 =
=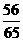 .
.
3 已知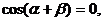 求证
求证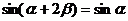 .
.
分析:比较已知与求证部分,必然要做如下变换为宜: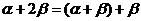 .
.
解: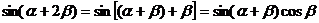 ,
,
而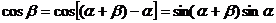 ,注意到
,注意到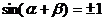 ,得
,得

例1(辅助角)函数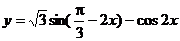 的最小值
的最小值
解: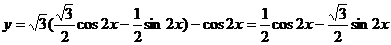
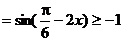
例2(角变换)已知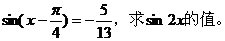
解: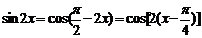
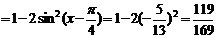
例3(公式逆用)计算:(1 +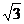 )tan15°-
)tan15°-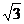
解:原式= (tan45°+ tan60°)tan15°-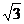
=tan105°(1-tan45°tan60°)tan15° -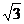
= (1 -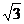 ) tan105° tan15° -
) tan105° tan15° -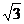 = (1 -
= (1 -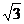 )×(- 1)-
)×(- 1)-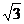 = - 1
= - 1
例4(角变换)已知sin(45° - a) = 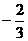 ,且45° < a < 90°,求sina
,且45° < a < 90°,求sina
解:∵45° <
a < 90° ∴-45° < 45°-a < 0° ∴cos(45°-a) = 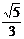
cos2a = sin(90°-2a) = sin[2(45°-a)]
= 2sin(45°-a)cos(45°-a) =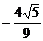
即 1 - sin2a = 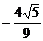 , 解之得:sina =
, 解之得:sina = 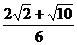
例5已知q是三角形中的一个最小的内角,
且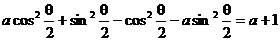 ,求a的取值范围
,求a的取值范围
解:原式变形: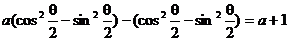
即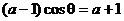 ,显然
,显然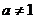 (若
(若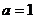 ,则 0 = 2)
,则 0 = 2)
∴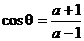
又∵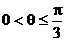 ,∴
,∴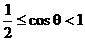
即 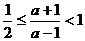 解之得:
解之得: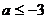
例6试求函数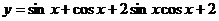 的最大值和最小值
的最大值和最小值 若
若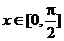 呢?
呢?
解:1.设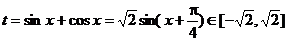
则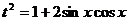 ∴
∴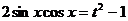
∴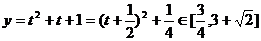
∴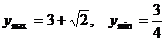
2.若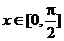 ,则
,则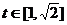 ,∴
,∴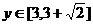
即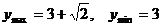
例7 已知tana = 3tan(a + b),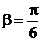 ,求sin(2a + b)的值
,求sin(2a + b)的值
解:由题设: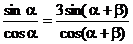 即sina cos(a + b) = 3sin(a + b)cosa
即sina cos(a + b) = 3sin(a + b)cosa
即sin(a + b) cosa + cos(a + b)sina = 2sina cos(a + b) - 2cosasin(a + b)
∴sin(2a + b) = -2sinb 又∵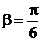 ∴sinb
∴sinb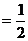 ∴sin(2a + b) = -1
∴sin(2a + b) = -1
1.两角和与差的正、余弦公式
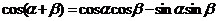
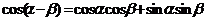
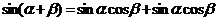
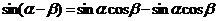
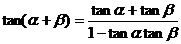
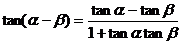
2 推导公式:
推导公式:
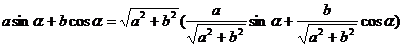
由于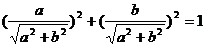
sin2θ+cos2θ=1
(1)若令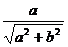 =sinθ,则
=sinθ,则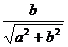 =cosθ
=cosθ
∴asinα+bcosα=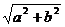 (sinθsinα+cosθcosα)=
(sinθsinα+cosθcosα)=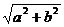 cos(θ-α)
cos(θ-α)
或=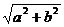 cos(α-θ)
cos(α-θ)
(2)若令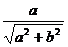 =cos
=cos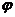 ,则
,则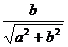 =sin
=sin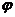
∴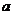 sinα+bcosα=
sinα+bcosα=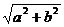 (sinαcos
(sinαcos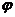 +cosαsin
+cosαsin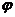 )=
)=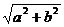 sin(α+
sin(α+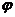 )
)
例如:2sinθ+cosθ=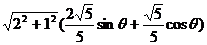
若令cos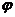 =
=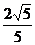 ,则sin
,则sin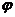 =
=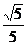
∴2sinθ+cosθ=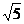 (sinθcos
(sinθcos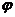 +cosθsin
+cosθsin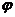 )=
)=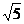 sin(θ+
sin(θ+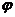 )
)
若令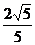 =sinβ,则
=sinβ,则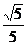 =cosβ
=cosβ
∴2sinθ+cosθ=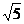 (cosθcosβ+sinθsinβ)=
(cosθcosβ+sinθsinβ)=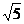 cos(θ-β)或
cos(θ-β)或
=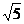 cos(β-θ)
cos(β-θ)
看来,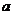 sinθ+bcosθ均可化为某一个角的三角函数形式,且有两种形式
sinθ+bcosθ均可化为某一个角的三角函数形式,且有两种形式
22.(本小题满分14分)已知函数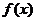 是一次函数,且
是一次函数,且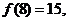
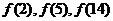 成等比数列,设
成等比数列,设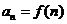 ,(
,( 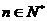 )
)
(1)求数列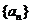 的前n项和Tn;
的前n项和Tn;
(2)设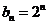 ,求数列
,求数列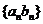 的前n项和
的前n项和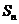 。
。
21.(本小题满分12分)
在等比数列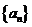 中,
中,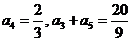 .
.
(I)求数列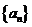 的通项公式;
的通项公式;
(II)若数列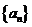 的公比大于
的公比大于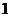 ,且
,且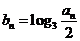 ,求数列
,求数列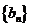 的前
的前 项和
项和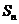 .
.
20.(本小题满分12分)
已知数列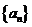 的前n项和公式为
的前n项和公式为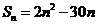 。
。
(1)这个数列是等差数列吗?求出它的通项公式;
(2)求使得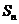 最小的序号n的值。
最小的序号n的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com