1．有效碰撞模型：

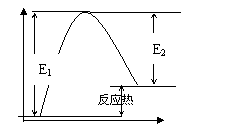分子间的磁撞并不一定就能发生化学反应，只有具有一定能量的微粒间的碰撞才可能是有效碰撞。

　人们把能够发生有效碰撞的分子叫做　　　 分子

1.内因(决定因素)：参加反应物质本身的性质

2外因：

⑴浓度：对气体或溶液中发生的化学反应，在其他条件不变时，　　　　　　　　　　 　

⑵压强：对有气体参加的化学反应，在其他条件不变时，　　　　　　　　　　　　

实质：

⑶温度：任何反应，在其他条件不变时，　　　　　 　　　　　　　　　　　　　

⑷催化剂是：在其他条件不变时，　　　　　　　　　　　　　　　　　　　　 。

⑸其它：搅拌、辐射、电弧、研磨和磁场等

[例3]下列因素中，对发生在溶液中且无气体参加的反应的速率不产生显著影响的是(　 )A.浓度　 B.温度C.压强D.反应物的性质

[例4]对于反应N₂+O₂＝2NO，在密闭容器中进行，下列哪些条件能加快该反应的速率(　 )

A.缩小体积使压强增大　　　　　　　　　 B.体积不变充入氮气使压强增大

C.体积不变充入氦气使压强增大　　　　　 D.压强不变充入氮气体积增大

[例5]NO和CO都是汽车尾气中的有害物质，它们能缓慢起反应，方程式为2CO+2NO=N₂+CO₂,为了控制大气污染，提出下列建议：　 A.使用催化剂B.改变压强C.提高反应温度

你认为可行的方法是，　　　　　 理由是　　　　　　　　　　　　　　　　 。

4.计算方法：(1)用定义式 (2)不同物质的速率比等于系数比

[例1]A与B反应生成C，假定反应由A、B开始，它们的起始浓度均为1 mol/L，反应进行2min后A的浓度为0.8 mol/L，B的浓度为0.6 mol/L，C的浓度为0.6 mol/L

(1)2min内反应的平均速率υ(A)=　　　　　　 υ(B) =　　 　　　　υ(C) =　　　　　　

(2)三者数值之间的关系是：υ(A)=　　 υ(B) =　　 υ(C)。

(3)该反应的化学方程式为　　　　　　　　　　　　　

[例2]一定温度下，向一个容积为2L的事先装入催化剂的真空密闭容器中通入1mol氮气和3mol氢气，3min后测得容器内的压强是起始时压强的0.9倍，在此时间内，用氢气的量的变化来表示该反应的平均速率为　 (　 )　　　　　　　　　　　　　　　　　　　　　 　　

　　 A．0.2mol·L^-1·min^-1　　　　　　 B．0.6mol·L^-1·min^-1

　　 C．0.1mol·L^-1·min^-1 D．0.3mol·L^-1·min^-1

3.特点：(1)是平均速率,均取正值;(2)　　 或　　　　 不适宜用来表示速率

(3)同一反应中用不同的物质表示的速率,其数值可能不同.但意义一样。

2. 公式：　　　　　　 单位：　　　　　　 　　。

1. 定义：用来衡量　　　　　　 的物理量，单位时间内　　　　　　　　　　　　　　

15．(2008·北京四中)已知：定义在(－1,1)上的函数f(x)满足：对任意x，y∈(－1,1)都有f(x)+f(y)＝f.

(1)求证：函数f(x)是奇函数；

(2)如果当x∈(－1,0)时，有f(x)>0，求证：f(x)在(－1,1)上是单调递减函数；

(3)在(2)的条件下解不等式：f+f>0.

(1)证明：令x＝y＝0，则f(0)+f(0)＝f(0)，故f(0)＝0.

令y＝－x，则f(x)+f(－x)＝f＝f(0)＝0，∴f(－x)＝－f(x)，

即函数f(x)是奇函数．

(2)证明：设x₁<x₂∈(－1,1)，则f(x₁)－f(x₂)＝f(x₁)+f(－x₂)＝f.

∵x₁<x₂∈(－1,1)，

∴x₂－x₁>0，－1<x₁x₂<1，

因此，<0，∴f>0，

即f(x₁)－f(x₂)>0.∴函数f(x)在(－1,1)上是单调递减函数．

(3)解：不等式f+f>0可化为f>f.

∵函数f(x)在(－1,1)上是减函数，

∴

解得：－<x<－1，

∴原不等式的解集为.

14．已知函数f(x)＝x²+|x－a|+1，a∈R.

(1)试判断f(x)的奇偶性；

(2)若－≤a≤，求f(x)的最小值．

解：(1)当a＝0时，

函数f(－x)＝(－x)²+|－x|+1＝f(x)，

此时，f(x)为偶函数．

当a≠0时，f(a)＝a²+1，f(－a)＝a²+2|a|+1，

f(a)≠f(－a)，f(a)≠－f(－a)，

此时，f(x)为非奇非偶函数．

(2)当x≤a时，f(x)＝x²－x+a+1

＝(x－)²+a+，

∵a≤，故函数f(x)在(－∞，a]上单调递减，

从而函数f(x)在(－∞，a]上的最小值为f(a)＝a²+1.

当x≥a时，函数f(x)＝x²+x－a+1

＝(x+)²－a+，

∵a≥－，故函数f(x)在[a，+∞)上单调递增，从而函数f(x)在[a，+∞)上的最小值为f(a)＝a²+1.

综上得，当－≤a≤时，

函数f(x)的最小值为a²+1.

13．已知f(x)是R上的奇函数，且当x∈(－∞，0)时，f(x)＝－xlg(2－x)，求f(x)的解析式．

解：∵f(x)是奇函数，可得f(0)＝－f(0)，∴f(0)＝0.

当x>0时，－x<0，由已知f(－x)＝xlg(2+x)，

∴－f(x)＝xlg(2+x)，

即f(x)＝－xlg(2+x) (x>0)，

∴f(x)＝

即f(x)＝－xlg(2+|x|)　(x∈R)．

12．已知f(x)是实数集R上的函数，且对任意x∈R，f(x)＝f(x+1)+f(x－1)恒成立．

(1)求证：f(x)是周期函数；

(2)已知f(3)＝2，求f(2004)．

(1)证明：∵f(x)＝f(x+1)+f(x－1)

∴f(x+1)＝f(x)－f(x－1)，

则f(x+2)＝f[(x+1)+1]＝f(x+1)－f(x)

＝f(x)－f(x－1)－f(x)＝－f(x－1)．

∴f(x+3)＝f[(x+1)+2]＝－f[(x+1)－1]＝－f(x)．

∴f(x+6)＝f[(x+3)+3]＝－f(x+3)＝f(x)．

∴f(x)是周期函数且6是它的一个周期．

(2)解：f(2004)＝f(334×6)＝f(0)＝－f(3)＝－2.