11．(2008·南通一中)已知函数f(x)是定义在R上的偶函数，定义在R上的奇函数g(x)过点(－1,1)，且g(x)＝f(x－1)，则f(7)+f(8)的值为________．

答案：－1

解析：由题意得g(0)＝0，g(－1)＝1，g(1)＝－1.又g(－x)＝－g(x)，

则f(－x－1)＝－f(x－1)，而f(－x)＝f(x)，则f(x+1)＝－f(x－1)，也得f(x－1)＝－f(x－3)，于是f(x+1)＝f(x－3),4为函数f(x)的周期，则f(－1)＝g(0)＝0，f(0)＝g(1)＝－1，f(7)+f(8)＝f(－1)+f(0)＝－1，故填－1.

10．设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)+f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是__________．

答案：(－∞，－3)∪(0,3)

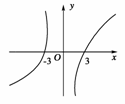
解析：设F(x)=f(x)·g(x)，

F(-x)=f(-x)g(-x)=-f(x)g(x)=-F(x)，

∴F(x)为奇函数．

又x<0时，F′(x)=f′(x)g(x)+f(x)g′(x)>0.

∴x<0时，F(x)为增函数．

∵奇函数在对称区间上单调性相同，

∴x>0时，F(x)为增函数．

∵F(-3)=f(-3)·g(-3)=0，

∴F(3)=-F(-3)=0.

如上图所示为一个符合题意的图象，观察知f(x)g(x)＝F(x)<0的解集为x∈(－∞，－3)∪(0,3)．

9．已知f(x)＝ax²+bx+3a+b是偶函数，定义域为[a－1,2a]，则a＝__________，b＝__________.

答案：　0

解析：∵y＝f(x)是偶函数，

∴∴故填　0.

8．(2009·江西省重点中学一次联考)已知定义域为R的函数y＝f(x)在(－∞，a)(a>0)上是增函数，且函数y＝f(x+a)是偶函数，当x₁<a，x₂>a，|x₁－a|<|x₂－a|时有(　)

A．f(2a－x₁)>f(2a－x₂)

B．f(2a－x₁)＝f(2a－x₂)

C．f(2a－x₁)<f(2a－x₂)

D．f(2a－x₁)与f(2a－x₂)的大小关系不确定

答案：A

解析：由y＝f(x+a)是偶函数得f(－x+a)＝f(x+a)，即f(x)＝f(2a－x)，于是f(x₁)＝f(2a－x₁)，f(x₂)＝f(2a－x₂)．由x₁<a，x₂>a，|x₁－a|<|x₂－a|得2a－x₂<a，a－x₁<x₂－a,2a－x₂<x₁<a.又函数f(x)在(－∞，a)上是增函数，因此有f(2a－x₂)<f(x₁)，f(2a－x₂)<f(2a－x₁)，选A.

7．(2009·西安地区八校联考)设函数f(x)、g(x)的定义域分别为F、G，且F?G.若对任意的x∈F，都有g(x)＝f(x)，则称g(x)为f(x)在G上的一个“延拓函数”．已知函数f(x)＝2^x(x≤0)，若g(x)为f(x)在R上的一个延拓函数，且g(x)是偶函数，则函数g(x)的解析式是(　)

A．2^|x|　 　　　　　　　　　　　　　　　　　　　　　　　 B．log₂|x|

C．()^|x|　 　　　　　　　　　　　　　　　　　　　　　　 D．log|x|

答案：C

解析：由题意得，当x≤0时，g(x)＝f(x)＝2^x＝2^－|x|.又g(x)是偶函数，因此有g(－x)＝g(x)恒成立．当x>0时，－x<0，g(x)＝g(－x)＝2^－x＝()^|x|.综上所述，g(x)＝()^|x|，选C.

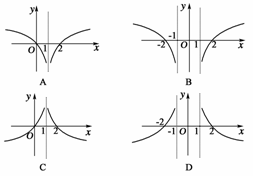
6．(2009·成都市一测)已知a>0，且a≠1，若函数f(x)＝log_a(x+)在(－∞，+∞)上既是奇函数，又是增函数，则函数g(x)＝log_a|x－k|的图象是(　)

5．(2008·湖北省八校联考)定义在R上的函数f(x)的图象关于点(－，0)成中心对称，对任意的实数x都有f(x)＝－f(x+)，且f(－1)＝1，f(0)＝－2，则f(1)+f(2)+f(3)+…+f(2008)的值为(　)

A．－2　 　　　　　　　　　　　　　　　　　　　　　　 B．－1

C．0　 　　　　　　　　　　　　　　　　　　　　　　　　 D．1

答案：D

解析：函数f(x)的图象关于点(－，0)成中心对称，得f(x)+f(－－x)＝0，又f(x)＝－f(x+)，于是f(x)是偶函数，且f(x)＝－f(x+)＝f(x+3)，即3是函数f(x)的周期，f(－1)＝1＝f(2)＝f(1)＝f(4)，f(0)＝－2＝f(3)，

f(1)+[f(2)+f(3)+f(4)]+…+[f(2006)+f(2007)+f(2008) ＝f(1)＝1.故选D.

4．(2009·徐水模拟)已知f(x)是以2为周期的奇函数，当0<x<1时，f(x)＝lgx，设a＝f()，b＝f()，c＝f()，则(　)

A．a<b<c　 　　　　　　　　　　　　　　　　　　　　 B．b<a<c

C．c<b<a　 　　　　　　　　　　　　　　　　　　　　 D．c<a<b

答案：D

解析：a＝f()＝－f(－)＝－f(－+2)＝－f()

b＝f()＝－f(－)＝－f()，c＝f()＝f()

由当0<x<1时，f(x)＝lgx得c<a<b.

3．(2008·北京市西城区抽样测试)设函数f(x)＝.若f(x)是奇函数，则g(2)的值是(　)

A．－　 　　　　　　　　　　　　　　　　　　　　　　 B．－4

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．4

答案：A

解析：∵f(x)是奇函数，∴f(－x)＝－f(x)；∵f(x)＝，当x>0时，－x<0，f(－x)＝－f(x)＝2^－x，∴g(x)＝－2^－x(x>0)，g(2)＝－，故选A.

2．(2009·北京市西城区4月)设a为常数，f(x)＝x²－4x+3，若函数f(x+a)为偶函数，则a等于(　)

A．－2　　　　　　　　　　　 B．2

C．－1 　　　　　　　　　　　　　　　　　　　　　　　 D．1

答案：B

解析：依题意，由f(x+a)＝(x+a)²－4(x+a)+3＝x²+(2a－4)x+(a²－4a+3)是偶函数，因此2a－4＝0，a＝2，选B.