
7.已知二面角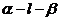 的大小为
的大小为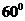 ,
,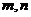 为异面直线,且
为异面直线,且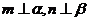 ,则
,则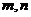 所成的角为
( B
)
所成的角为
( B
)
A.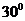 B.
B.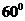 C.
C.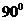 D.
D.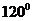
6.二面角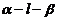 内有一点P,若P到平面
内有一点P,若P到平面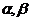 的距离分别是5,8,且P在平面
的距离分别是5,8,且P在平面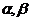 的内的射影间的距离为7,则二面角
的内的射影间的距离为7,则二面角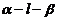 的度数是
( C
)
的度数是
( C
)
A.300 B.600 C.1200 D.1500
5.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( A )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
4.已知异面直线a与b所成的角为50º,P为空间一定点,则过点P且与a、b所成的角都是30º的直线有且仅有 ( B )
A.1条 B.2条 C.3条 D.4条
3.已知两条异面直线所成的角为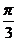 ,直线c与a,b所成的角都是
,直线c与a,b所成的角都是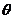 ,则
,则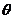 的取值范围是
的取值范围是
( B )
A.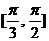 B.
B.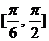 C.
C.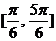 D.
D.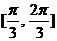
2.正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是 ( C )
A.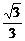 B.
B.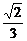 C.
C.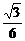 D.
D.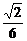
1.空间两直线l、m在平面α、β上射影分别为a1、b1和a2、b2.若a1∥b1,a2与b2交于 一点,则l和m的位置关系为 ( A )
A.一定异面 B.一定平行 C.异面或相交 D.平行或异面
10.如图,AB是圆O的直径,C是圆周上一点,PA⊥平面ABC.
(1)求证:平面PAC⊥平面PBC;
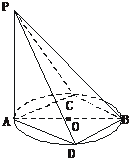
(2)若D也是圆周上一点,且与C分居直径AB的两侧,试写出图中所有互相垂直的各对平面.
(2)解:平面PAC⊥平面ABCD;平面PAC⊥平面PBC;平面PAD⊥平面PBD;平面PAB⊥平面ABCD;平面PAD⊥平面ABCD.
考查平面与平面位置关系.要求掌握平面与平面平行、垂直的判定定理和性质定理.会运用三垂线定理及其逆定理研究空间的垂直关系.会运用 “转化”、“降维”等思想方法进行“线线”“线面”“面面”间的垂直与平行关系的转化.
9. 如图,在四棱锥
如图,在四棱锥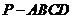 中,
中,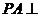 底面
底面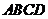 ,底面各边都相等,
,底面各边都相等,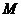 是
是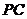 上的一动点,当点
上的一动点,当点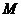 满足_______时,平面
满足_______时,平面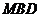
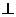 平面
平面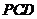 。OM
。OM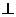 PC,(MD
PC,(MD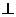 PC,MB
PC,MB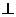 PC)
PC)
8.已知a、b为两条不同的直线,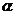 、β为两个不同的平面,且a⊥
、β为两个不同的平面,且a⊥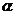 ?b⊥β,则下列命题中的假命题是
( D )
?b⊥β,则下列命题中的假命题是
( D )
A.若a∥b,则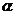 ∥β
B.若
∥β
B.若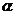 ⊥β,则a⊥b
⊥β,则a⊥b
C.若a,b相交,则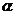 、β相交 D.若
、β相交 D.若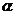 、β相交,则a、b相交
、β相交,则a、b相交
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com