
∴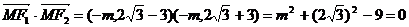
由双曲线x2-y2=6知F1(2 ,0),F2(-2
,0),F2(-2 ,0)
,0)
知 =42-(-
=42-(- )2=6
)2=6
∴双曲线方程为x2-y2=6
(2)若点M(3,m)在双曲线上
则32-m2=6 ∴m2=3
则由点(4,- )在双曲线上
)在双曲线上
∴设所求双曲线方程为x2-y2= (
( ≠0)
≠0)
解:(1) ∵离心率e=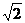
40、(广东省四校联合体第一次联考)已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,- )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F
(3)求△F1MF2的面积.
故由 ,即
,即 ,解之得
,解之得 的取值范围是
的取值范围是 .
.
 ,
,
设直线 :
: (其中
(其中 ),则
),则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com