
(18)(本题满分14分)在 ABC中,角A、B、C所对应的边分别为a、b、c,且满足
ABC中,角A、B、C所对应的边分别为a、b、c,且满足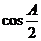 =
=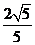 ,
,
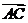 =3.
=3.
(Ⅰ)求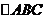 的面积;
的面积; 

(Ⅱ)若b+c=6,求a的值。
(19)(本题满分14分)在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率; 

(Ⅱ)记ξ为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时ξ的值是2)。求随机变量ξ的分布列及其数学期望Eξ.
(20)(本题满分15分)如图,平面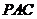 ⊥平面
⊥平面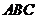 ,
,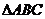 是以
是以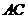 为斜边的等腰直角三角形。
为斜边的等腰直角三角形。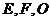 分别为
分别为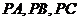 的中点,
的中点,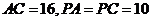 。
。
(I) 设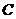 是
是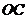 的中点,证明:
的中点,证明: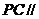 平面
平面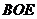 ;
; 

(II)证明:在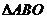 内存在一点
内存在一点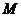 ,使
,使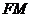 ⊥平面
⊥平面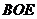 ,并求点
,并求点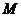 到
到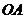 ,
,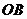 的距离。
的距离。
(21)(本题满分15分)已知椭圆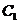 :
: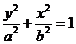 (
(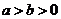 )的右顶点
)的右顶点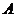 (1,0),过
(1,0),过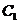 的焦点且垂直长轴的弦长为1。
的焦点且垂直长轴的弦长为1。 

(I) 求椭圆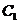 的方程;
的方程;
(II) 设点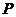 在抛物线
在抛物线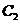 :
: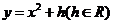 上,
上,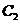 在点P处的切线与
在点P处的切线与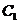 交于点
交于点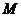 ,
,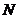 。当线段AP的中点与MN的中点的横坐标相等时,求
。当线段AP的中点与MN的中点的横坐标相等时,求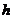 的最小值。
的最小值。
(22)(本题满分14分)已知函数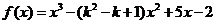 ,
,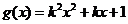 ,其中
,其中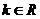 。
。
(I) 设函数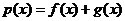 。若
。若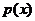


(II)设函数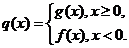 是否存在
是否存在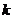 ,对任意给定的非零实数
,对任意给定的非零实数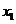 ,存在惟一的非零实数
,存在惟一的非零实数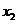 (
(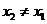 ),使得
),使得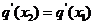 ?若存在,求
?若存在,求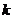 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(11)设等比数列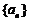 的公比
的公比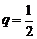 ,前n项和为
,前n项和为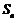 ,
,
则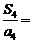 _____________.
_____________.


(12)若某几何体的三视图(单元:cm)如图所示,则
此几何体的体积是________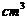 .
.
(13)若实数x,y满足不等式组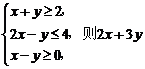
的最小值是__________.
(14)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
|
低谷时间段用电价格表 |
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
|
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
50及以下的部分 |
0.568 |
|
50及以下的部分 |
0.288 |
|
超过50至200的部分 |
0.598 |
|
超过50至200的部分 |
0.318 |
|
超过200的部分 |
0.668 |
|
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答)。
观察下列等式:
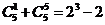 ,
,
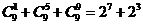 ,
,
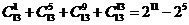 ,
,
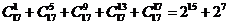 ,
,
……
由以上等式推测到一个一般的结论:
对于n∈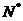 ,
,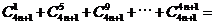 _________.
_________. 

(16)甲、乙、丙三人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是________(用数字作答)
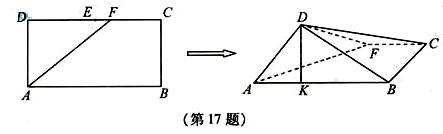
(17)如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将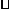 AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
(1)
设U=R,
(A)
 (B)
(B)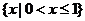 (C)
(C)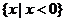 (D)
(D)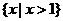
(2)已知a、b是实数,则“a>0,b>0”是a+b>0且ab>0的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件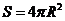
(3)设z=1+i(i是虚数单位),则
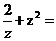
 (A)-1-i (B)-1+ i (C)1- i (D)1+i
(A)-1-i (B)-1+ i (C)1- i (D)1+i
(4)在二项式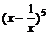 的展开式中,含x4的项的系数是
的展开式中,含x4的项的系数是
(A)-10 (B)10
(C)-5 (D)5
(5)在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D式侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是
(A)300 (B)450
(C)600 (D)900
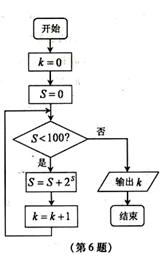
(6)某程序框图如图所示,该程序运行后输出的k的值是
(A)4 (B)5 (C)6 (D)7 

(7)设向量a,b满足︱a︱=3,︱b︱=4,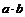 =0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
=0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
(A)3 (B)4 (C)5 (D)6
(8)已知a是实数,则函数f(x)=1+asinax的图像不可能是
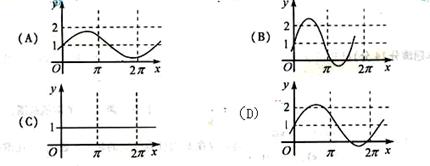
(9)过双曲线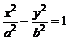 (a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若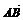 =
=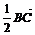 ,则双曲线的离心率是
,则双曲线的离心率是 

(A)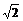 (B)
(B)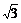 (C)
(C)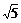 (D)
(D)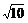
(10)对于正实数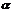 ,记M
,记M 为满足下述条件的函数f(x)构成的集合:
为满足下述条件的函数f(x)构成的集合: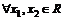 且
且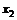 >
>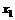 ,有-
,有-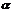 (
(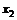 -
-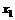 )<f(
)<f(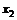 )-f(
)-f(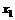 )<
)<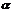 (
(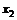 -
-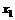 ).下列结论正确的是
).下列结论正确的是
(A)若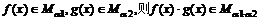
(B)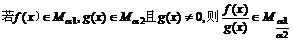
(C)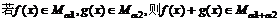


(D)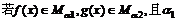 >
>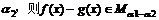
2009年普通高等学校招生全国统一考试
数学(理科)
非选择题部分(共100分)
(18)(本题满分14分)在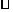 ABC中,角A、B、C所对应的边分别为a、b、c,且满足
ABC中,角A、B、C所对应的边分别为a、b、c,且满足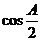 =
=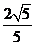 ,
,
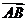
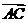 =3.
=3.
(Ⅰ)求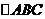 的面积;
的面积; 

(Ⅱ)若b+c=6,求a的值。
(19)(本题满分14分)在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率; 

(Ⅱ)记ξ为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时ξ的值是2)。求随机变量ξ的分布列及其数学期望Eξ.
(20)(本题满分15分)如图,平面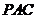 ⊥平面
⊥平面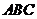 ,
,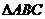 是以
是以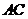 为斜边的等腰直角三角形。
为斜边的等腰直角三角形。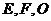 分别为
分别为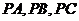 的中点,
的中点,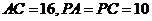 。
。
(I) 设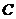 是
是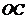 的中点,证明:
的中点,证明: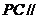 平面
平面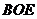 ;
; 

(II)证明:在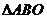 内存在一点
内存在一点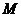 ,使
,使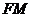 ⊥平面
⊥平面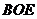 ,并求点
,并求点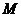 到
到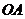 ,
,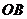 的距离。
的距离。
(21)(本题满分15分)已知椭圆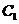 :
: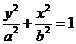 (
(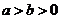 )的右顶点
)的右顶点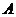 (1,0),过
(1,0),过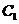 的焦点且垂直长轴的弦长为1。
的焦点且垂直长轴的弦长为1。 

(I) 求椭圆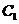 的方程;
的方程;
(II) 设点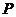 在抛物线
在抛物线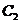 :
: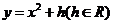 上,
上,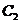 在点P处的切线与
在点P处的切线与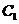 交于点
交于点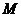 ,
,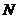 。当线段AP的中点与MN的中点的横坐标相等时,求
。当线段AP的中点与MN的中点的横坐标相等时,求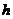 的最小值。
的最小值。
(22)(本题满分14分)已知函数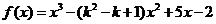 ,
,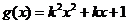 ,其中
,其中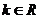 。
。
(I) 设函数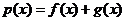 。若
。若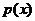


(II)设函数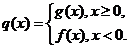 是否存在
是否存在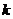 ,对任意给定的非零实数
,对任意给定的非零实数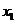 ,存在惟一的非零实数
,存在惟一的非零实数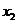 (
(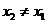 ),使得
),使得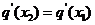 ?若存在,求
?若存在,求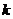 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(11)设等比数列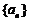 的公比
的公比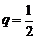 ,前n项和为
,前n项和为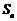 ,
,
则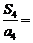 _____________.
_____________.


(12)若某几何体的三视图(单元:cm)如图所示,则
此几何体的体积是________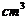 .
.
(13)若实数x,y满足不等式组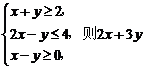
的最小值是__________.
(14)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
|
低谷时间段用电价格表 |
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
|
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
50及以下的部分 |
0.568 |
|
50及以下的部分 |
0.288 |
|
超过50至200的部分 |
0.598 |
|
超过50至200的部分 |
0.318 |
|
超过200的部分 |
0.668 |
|
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答)。
观察下列等式:
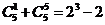 ,
,
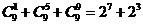 ,
,
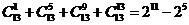 ,
,
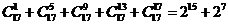 ,
,
……
由以上等式推测到一个一般的结论:
对于n∈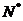 ,
,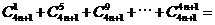 _________.
_________. 

(16)甲、乙、丙三人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是________(用数字作答)
(17)如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将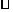 AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是_______.
(1)
设U=R,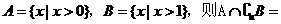
(A)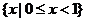
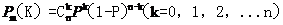 (B)
(B)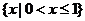 (C)
(C)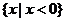 (D)
(D)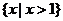
(2)已知a、b是实数,则“a>0,b>0”是a+b>0且ab>0的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件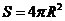
(3)设z=1+i(i是虚数单位),则
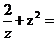
 (A)-1-i (B)-1+ i (C)1- i (D)1+i
(A)-1-i (B)-1+ i (C)1- i (D)1+i
(4)在二项式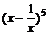 的展开式中,含x4的项的系数是
的展开式中,含x4的项的系数是
(A)-10 (B)10
(C)-5 (D)5
(5)在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D式侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是
(A)300 (B)450
(C)600 (D)900
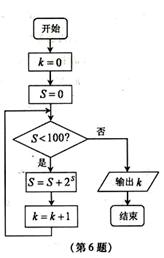
(6)某程序框图如图所示,该程序运行后输出的k的值是
(A)4 (B)5 (C)6 (D)7 

(7)设向量a,b满足︱a︱=3,︱b︱=4,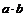 =0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
=0.以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为
(A)3 (B)4 (C)5 (D)6
(8)已知a是实数,则函数f(x)=1+asinax的图像不可能是
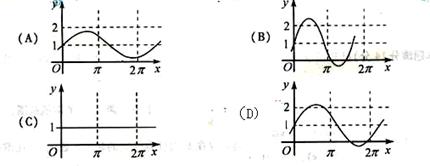
(9)过双曲线 (a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若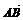 =
=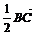 ,则双曲线的离心率是
,则双曲线的离心率是 

(A)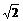 (B)
(B)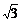 (C)
(C)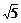 (D)
(D)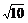
(10)对于正实数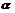 ,记M
,记M 为满足下述条件的函数f(x)构成的集合:
为满足下述条件的函数f(x)构成的集合: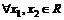 且
且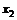 >
>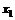 ,有-
,有-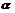 (
(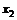 -
-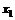 )<f(
)<f(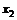 )-f(
)-f(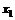 )<
)<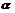 (
(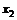 -
-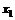 ).下列结论正确的是
).下列结论正确的是
(A)若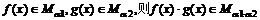
(B)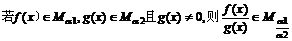
(C)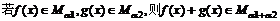


(D)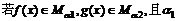 >
>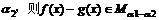
2009年普通高等学校招生全国统一考试
数学(理科)
非选择题部分(共100分)
(17)(本小题满分12分)
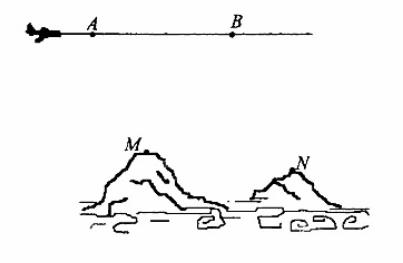
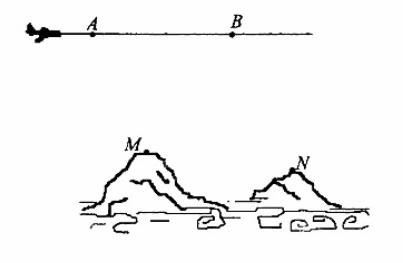
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
(18)(本小题满分12分)
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; 

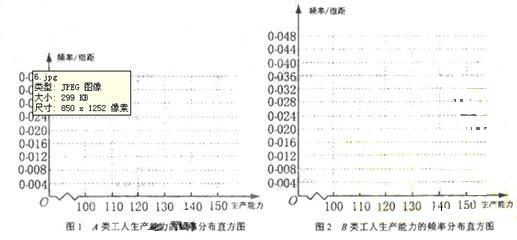
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.

(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论) 

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表) 

(19)(本小题满分12分)
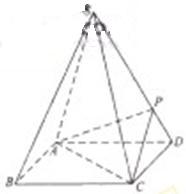 如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的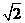 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD; 

(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 

使得BE∥平面PAC。若存在,求SE:EC的值;
若不存在,试说明理由。
(20)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,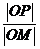 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。 

(21)(本小题满分12分)
已知函数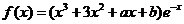
(I)
如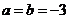 ,求
,求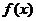 的单调区间;
的单调区间;
(II)
若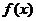 在
在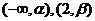 单调增加,在
单调增加,在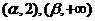 单调减少,证明
单调减少,证明
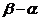 <6.
<6. 

请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
(22)本小题满分10分)选修4-1:几何证明选讲 

如图,已知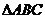 的两条角平分线
的两条角平分线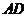 和
和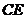 相交于H,
相交于H,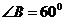 ,F在
,F在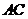 上,
上,
且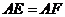 。
。
(I) 证明:B,D,H,E四点共圆:
(II)
证明: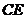 平分
平分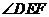 。
。 

(23)(本小题满分10分)选修4-4:坐标系于参数方程
已知曲线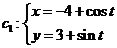 (t为参数),
(t为参数), 

(24)(本小题满分10分)选修4-5:不等式选讲
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值? 


(13)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线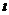 的方程为_____________.
的方程为_____________.
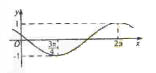 (14)已知函数y=sin(
(14)已知函数y=sin(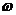 x+
x+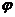 )(
)(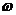 >0, -
>0, -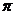
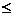
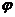 <
<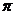 )的图像如图所示,则
)的图像如图所示,则 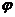 =________________
=________________
(15)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
(16)等差数列{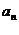 }前n项和为
}前n项和为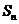 。已知
。已知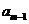 +
+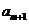 -
-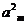 =0,
=0,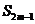 =38,则m=_______
=38,则m=_______
(17)(本小题满分12分)
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
(18)(本小题满分12分)
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; 

(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.

(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论) 

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表) 

(19)(本小题满分12分)
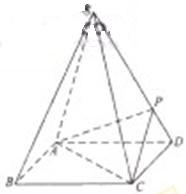 如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的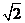 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD; 

(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 

使得BE∥平面PAC。若存在,求SE:EC的值;
若不存在,试说明理由。
(20)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,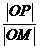 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。 

(21)(本小题满分12分)
已知函数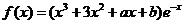
(I)
如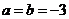 ,求
,求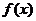 的单调区间;
的单调区间;
(II)
若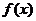 在
在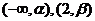 单调增加,在
单调增加,在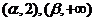 单调减少,证明
单调减少,证明
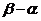 <6.
<6. 

请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
(22)本小题满分10分)选修4-1:几何证明选讲 

如图,已知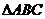 的两条角平分线
的两条角平分线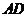 和
和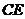 相交于H,
相交于H,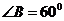 ,F在
,F在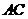 上,
上,
且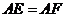 。
。
(I) 证明:B,D,H,E四点共圆:
(II)
证明: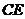 平分
平分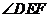 。
。 

(23)(本小题满分10分)选修4-4:坐标系于参数方程
已知曲线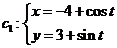 (t为参数),
(t为参数), 

(24)(本小题满分10分)选修4-5:不等式选讲
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值? 


(13)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线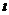 的方程为_____________.
的方程为_____________.
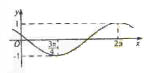 (14)已知函数y=sin(
(14)已知函数y=sin(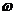 x+
x+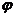 )(
)(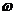 >0, -
>0, -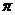
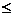
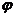 <
<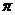 )的图像如图所示,则
)的图像如图所示,则 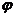 =________________
=________________
(15)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
(16)等差数列{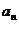 }前n项和为
}前n项和为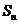 。已知
。已知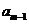 +
+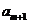 -
-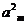 =0,
=0,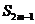 =38,则m=_______
=38,则m=_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com