
(16)(本小题满分12分)
在△ABC中,sin(C-A)=1,sinB=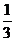 .
.
(Ⅰ)求sinA的值;
(Ⅱ)设AC=,求△ABC的面积.


(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的。对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是1/2.同样也假设D受A、B和C感染的概率都是1/3.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(18)(本小题满分13分)
如图,四棱椎F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.
(Ⅰ) 求二面角B-AF-D的大小;
(Ⅱ) 求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。 

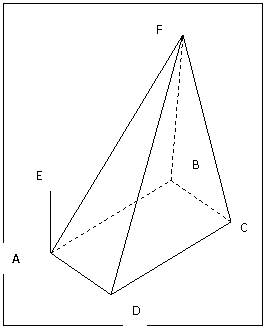
第(18)题图
(19)(本小题满分12分)
已知函数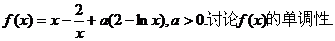


(20)(本小题满分13分)
点P(x0,y0)在椭圆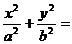 1(a>b>0)上,x0=
1(a>b>0)上,x0=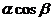 , y0=
, y0= . 直线
. 直线 与直线
与直线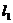 :
: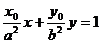 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为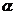 ,直线
,直线 的倾斜角为
的倾斜角为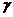 .
.
(Ⅰ)证明:点P是椭圆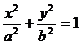 与直线
与直线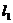 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan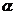 ,tan
,tan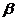 ,tan
,tan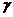 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列{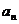 }满足
}满足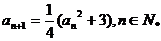 .
.
(Ⅰ)证明:若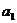 为奇数,则对一切
为奇数,则对一切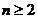 ,
,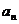 都是奇数;
都是奇数;
(Ⅱ)若对一切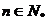 ,都有
,都有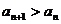 ,求
,求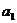 的取值范围。
的取值范围。
W数学(理科)试题 第4页(共4页) 

(11)若随机变量X~N(μ,σ2),则P(X≤μ)= .
(12)以直角坐标系的原点为极点,x轴的正半轴为极轴, 

并在两种坐标系中取相同的长度单位,已知直线的
 极坐标方程为
极坐标方程为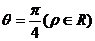 ,它与曲线
,它与曲线
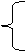
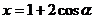
(α为参数)相交于两点A和B,则
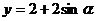
|AB|= .
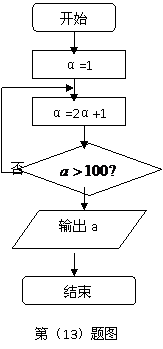
(13)程序框图(即算法流程图)如图所示,其输出结果是
.
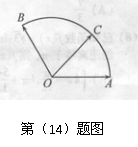
(14)给定两个长度为1的平面向量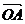 和
和 ,它们的夹
,它们的夹
角为120°.如图所示,点C在以O为圆心的圆弧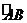
上变动.若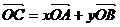 ,其中
,其中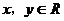 ,则x+y
,则x+y
的最大值是 .
 (15)对于四面体ABCD,下列命题正确的是
(15)对于四面体ABCD,下列命题正确的是
(写出所有正确命题的编号).
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
(1)i是虚数单位,若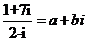 (a、b∈R),则乘积ab的值是
(a、b∈R),则乘积ab的值是
(A)-15 (B)-3 (C)3 (D)15
(2)若集合A={x|︱2x-1︱<3},B={x|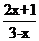 <0},则A∩B是
<0},则A∩B是
(A){x|-1<x<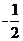 或2<x<3} (B){x|2<x<3}
或2<x<3} (B){x|2<x<3}
(C){x|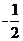 <x<2}
(D){x|-1<x<
<x<2}
(D){x|-1<x<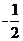 }
}
 (3)下列曲线中离心率为
(3)下列曲线中离心率为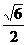 的是
的是
(A)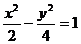 (B)
(B)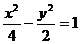
(C)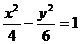 (D)
(D)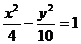

(4)下列选项中,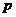 是
是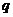 的必要不充分条件的是
的必要不充分条件的是
(A)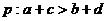 ,
, 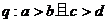
(B)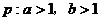 ,
, 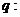
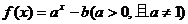 的图像不过第二象限
的图像不过第二象限
(C)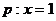 ,
,
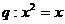
(D)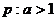 ,
,
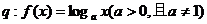 在
在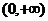 上为增函数
上为增函数
(5)已知 为等差数列,
为等差数列,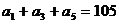 ,
,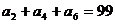 。以
。以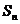 表示
表示 的前n项和,则使得
的前n项和,则使得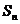 达到最大值的n是
达到最大值的n是
(A)21 (B)20 (C)19 (D)18
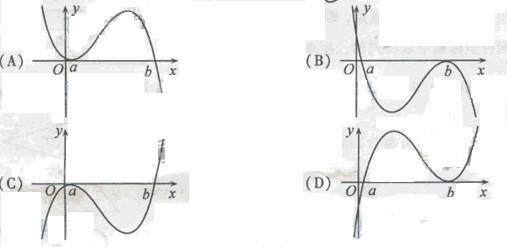
(6)设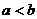 ,函数
,函数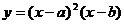 的图像可能是
的图像可能是
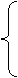
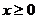
(7)若不等式组
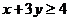 所表示的平面区域被直线
所表示的平面区域被直线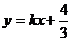 分为面积相等的两
分为面积相等的两
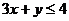
部分,则k的值是
(A)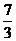 (B)
(B)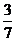 (C)
(C)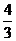 (D)
(D)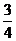
(8)已知函数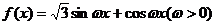 ,
,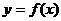 的图像与直线
的图像与直线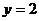 的两个相邻交点的距离等于
的两个相邻交点的距离等于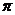 ,则
,则 的单调递增区间是
的单调递增区间是
(A)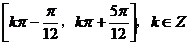 (B)
(B)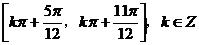
(C)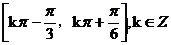 (D)
(D)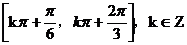
(9)已知函数 在R上满足
在R上满足 ,则曲线
,则曲线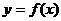 在点
在点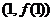 处的切线方程是
处的切线方程是
(A)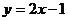
 (B)
(B)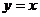 (C)
(C)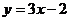 (D)
(D)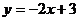
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)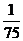 (B)
(B)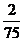 (C)
(C)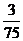 (D)
(D)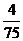
(在此卷上答题无效)
2009年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
(16)(本小题满分12分)
在△ABC中,sin(C-A)=1,sinB=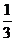 .
.
(Ⅰ)求sinA的值;
(Ⅱ)设AC=,求△ABC的面积.


(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的。对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是1/2.同样也假设D受A、B和C感染的概率都是1/3.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(18)(本小题满分13分)
如图,四棱椎F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.
(Ⅰ) 求二面角B-AF-D的大小;
(Ⅱ) 求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。 

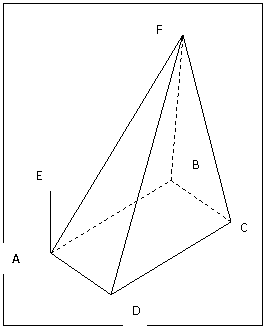
第(18)题图
(19)(本小题满分12分)
已知函数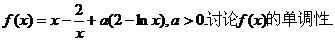


(20)(本小题满分13分)
点P(x0,y0)在椭圆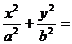 1(a>b>0)上,x0=
1(a>b>0)上,x0=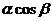 , y0=
, y0=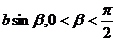 . 直线
. 直线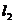 与直线
与直线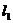 :
: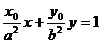 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为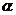 ,直线
,直线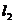 的倾斜角为
的倾斜角为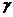 .
.
(Ⅰ)证明:点P是椭圆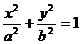 与直线
与直线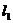 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan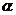 ,tan
,tan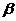 ,tan
,tan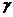 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列{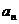 }满足
}满足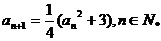 .
.
(Ⅰ)证明:若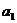 为奇数,则对一切
为奇数,则对一切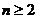 ,
,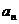 都是奇数;
都是奇数;
(Ⅱ)若对一切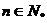 ,都有
,都有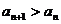 ,求
,求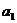 的取值范围。
的取值范围。
W数学(理科)试题 第4页(共4页) 

(11)若随机变量X~N(μ,σ2),则P(X≤μ)= .
(12)以直角坐标系的原点为极点,x轴的正半轴为极轴, 

并在两种坐标系中取相同的长度单位,已知直线的
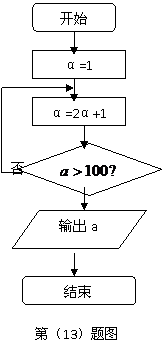 极坐标方程为
极坐标方程为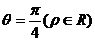 ,它与曲线
,它与曲线
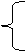
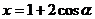
(α为参数)相交于两点A和B,则
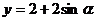
|AB|= .
(13)程序框图(即算法流程图)如图所示,其输出结果是
.
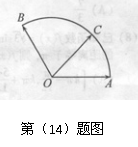
(14)给定两个长度为1的平面向量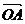 和
和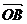 ,它们的夹
,它们的夹
角为120°.如图所示,点C在以O为圆心的圆弧
上变动.若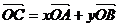 ,其中
,其中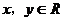 ,则x+y
,则x+y
的最大值是 .
 (15)对于四面体ABCD,下列命题正确的是
(15)对于四面体ABCD,下列命题正确的是
(写出所有正确命题的编号).
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
(1)i是虚数单位,若 (a、b∈R),则乘积ab的值是
(a、b∈R),则乘积ab的值是
(A)-15 (B)-3 (C)3 (D)15
(2)若集合A={x|︱2x-1︱<3},B={x|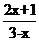 <0},则A∩B是
<0},则A∩B是
(A){x|-1<x<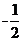 或2<x<3} (B){x|2<x<3}
或2<x<3} (B){x|2<x<3}
(C){x|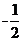 <x<2}
(D){x|-1<x<
<x<2}
(D){x|-1<x<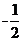 }
}
 (3)下列曲线中离心率为
(3)下列曲线中离心率为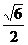 的是
的是
(A)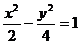 (B)
(B)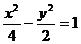
(C)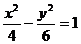 (D)
(D)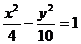

(4)下列选项中,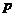 是
是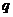 的必要不充分条件的是
的必要不充分条件的是
(A)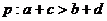 ,
, 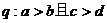
(B)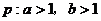 ,
, 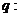
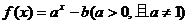 的图像不过第二象限
的图像不过第二象限
(C)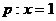 ,
,
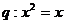
(D)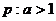 ,
,
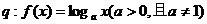 在
在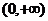 上为增函数
上为增函数
(5)已知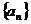 为等差数列,
为等差数列,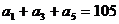 ,
, 。以
。以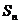 表示
表示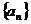 的前n项和,则使得
的前n项和,则使得 达到最大值的n是
达到最大值的n是
(A)21 (B)20 (C)19 (D)18
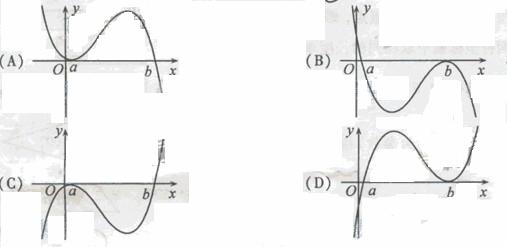
(6)设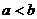 ,函数
,函数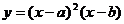 的图像可能是
的图像可能是
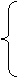
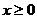
(7)若不等式组
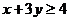 所表示的平面区域被直线
所表示的平面区域被直线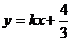 分为面积相等的两
分为面积相等的两
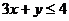
部分,则k的值是
(A)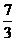 (B)
(B)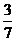 (C)
(C)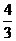 (D)
(D)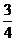
(8)已知函数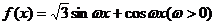 ,
, 的图像与直线
的图像与直线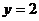 的两个相邻交点的距离等于
的两个相邻交点的距离等于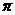 ,则
,则 的单调递增区间是
的单调递增区间是
(A)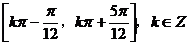 (B)
(B)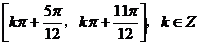
(C)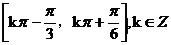 (D)
(D)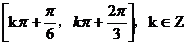
(9)已知函数 在R上满足
在R上满足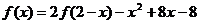 ,则曲线
,则曲线 在点
在点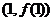 处的切线方程是
处的切线方程是
(A)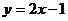
 (B)
(B)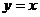 (C)
(C)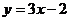 (D)
(D)
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)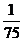 (B)
(B)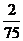 (C)
(C)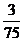 (D)
(D)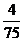
(在此卷上答题无效)
2009年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
17(本小题满分10分)
设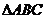 的内角
的内角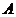 、
、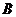 、
、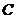 的对边长分别为
的对边长分别为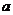 、
、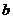 、
、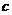 ,
,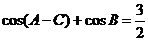 ,
,
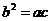 ,求
,求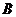 。
。
18(本小题满分12分)
如图,直三棱柱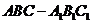 中,
中,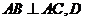 、
、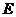 分别为
分别为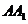 、
、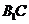 的中点,
的中点,
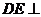 平面
平面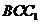


(I)证明: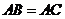
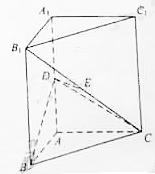 (II)设二面角
(II)设二面角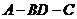 为60°,求
为60°,求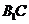 与平面
与平面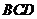 所成的角的大小。
所成的角的大小。
19(本小题满分12分)
设数列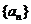 的前
的前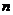 项和为
项和为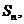 已知
已知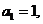
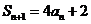
(I)设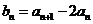 ,证明数列
,证明数列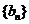 是等比数列
是等比数列 

(II)求数列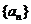 的通项公式。
的通项公式。
20(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数; 

(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记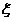 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求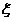 的分布列及数学期望。
的分布列及数学期望。
(21)(本小题满分12分)
已知椭圆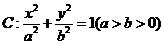 的离心率为
的离心率为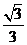 ,过右焦点F的直线
,过右焦点F的直线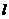 与
与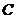 相交于
相交于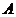 、
、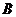 粮店,当
粮店,当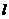 的斜率为1时,坐标原点
的斜率为1时,坐标原点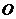 到
到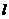 的距离为
的距离为


(I)求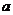 ,
,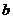 的值;
的值;
(II)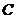 上是否存在点P,使得当
上是否存在点P,使得当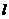 绕F转到某一位置时,有
绕F转到某一位置时,有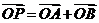 成立?
成立?
若存在,求出所有的P的坐标与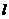 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
22.(本小题满分12分)
设函数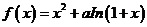 有两个极值点
有两个极值点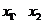 ,且
,且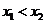
(I)求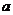 的取值范围,并讨论
的取值范围,并讨论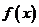 的单调性;
的单调性;
(II)证明: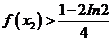










16. 已知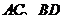 为圆
为圆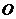 :
: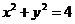 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为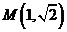 ,则四边形
,则四边形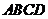 的面积的最大值为
。
的面积的最大值为
。
15.设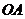 是球
是球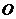 的半径,
的半径,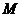 是
是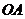 的中点,过
的中点,过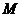 且与
且与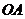 成45°角的平面截球
成45°角的平面截球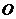 的表面得到圆
的表面得到圆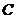 。若圆
。若圆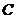 的面积等于
的面积等于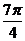 ,则球
,则球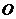 的表面积等于
的表面积等于
14. 设等差数列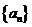 的前
的前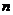 项和为
项和为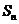 ,若
,若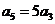 则
则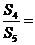 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com