
例2:物体A质量为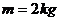 ,用两根轻绳B、C连接到竖直墙上,在物体A上加一恒力F,若图2中力F、轻绳AB与水平线夹角均为
,用两根轻绳B、C连接到竖直墙上,在物体A上加一恒力F,若图2中力F、轻绳AB与水平线夹角均为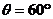 ,要使两绳都能绷直,求恒力F的大小。
,要使两绳都能绷直,求恒力F的大小。
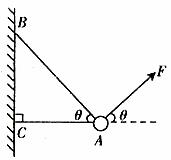
图2
解析:要使两绳都能绷直,必须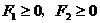 ,再利用正交分解法作数学讨论。作出A的受力分析图3,由正交分解法的平衡条件:
,再利用正交分解法作数学讨论。作出A的受力分析图3,由正交分解法的平衡条件:
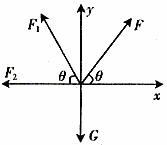
图3
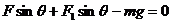 ①
①
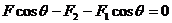 ②
②
解得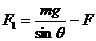 ③
③
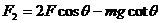 ④
④
两绳都绷直,必须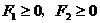
由以上解得F有最大值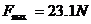 ,解得F有最小值
,解得F有最小值 ,所以F的取值为
,所以F的取值为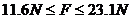 。
。
例1:图1中重物的质量为m,轻细线AO和BO的A、B端是固定的。平衡时AO是水平的,BO与水平面的夹角为θ。AO的拉力F1和BO的拉力F2的大小是( )
A. 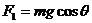 B.
B.
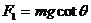
C. 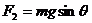 D.
D.
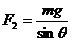
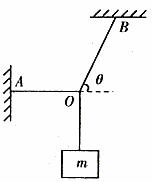
图1
解析:以“结点”O为研究对象,沿水平、竖直方向建立坐标系,在水平方向有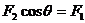 竖直方向有
竖直方向有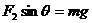 联立求解得BD正确。
联立求解得BD正确。
思考:若题中三段细绳不可伸长且承受的最大拉力相同,逐渐增加物体的质量m,则最先断的绳是哪根?
22.(14分)
已知函数f(x)=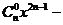
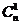
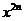
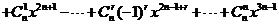 ,
,
其中n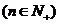 .
.
(1)求函数f(x)的极大值和极小值;
(2)设函数f(x)取得极大值时x=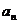 ,令
,令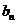 =2
=2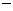 3
3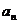 ,
,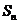 =
=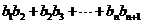 ,若p≤
,若p≤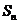 <q对一切n∈N+恒成立,求实数p和q的取值范围.
<q对一切n∈N+恒成立,求实数p和q的取值范围.
21.(12分)
在平面直角坐标系xoy中,点P到M(0,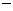
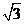 ),N(0,
),N(0,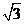 )的距离之和等于4,设点P的轨迹C.
)的距离之和等于4,设点P的轨迹C.
(1)写出曲线C的方程;
(2)设直线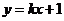 与曲线C交于A、B两点,k为何值时?
与曲线C交于A、B两点,k为何值时?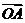
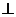
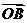 ,此时
,此时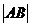 的值是多少?
的值是多少?
20.(12分)
已知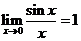 ,若函数,f(x)=
,若函数,f(x)=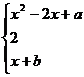
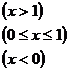 在R上连续.
在R上连续.
求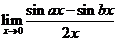 .
.
19.(12分)
如图,在正方体ABCD
-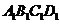 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面 的中心 .
的中心 .
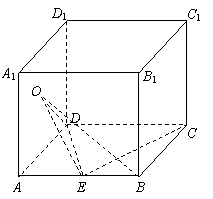 (1)求证:OB⊥EC ;
(1)求证:OB⊥EC ;
(2)求二面角O-DE-A的大小(用反三角函数表示).
18.
 (12分)射击运动员在双向飞碟射击比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个得1分,未击中0分.某运动员在每轮比赛时,第一枪命中率为
,第二枪命中率为 ,该运动员如进行两轮比赛.
(12分)射击运动员在双向飞碟射击比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个得1分,未击中0分.某运动员在每轮比赛时,第一枪命中率为
,第二枪命中率为 ,该运动员如进行两轮比赛.
(1)求该运动员得4分的概率;
(2)若该运动员所得分数为ξ , 求ξ的分布列及数学期望.
17.(12分)求不等式的解集:
(1)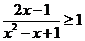 ;
;
(2)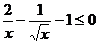 .
.
16.已知函数f(x)=1+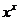 ,则f′(1)= .
,则f′(1)= .
15.已知函数y= f(x)的图像的两个对称中心分别是M(2,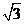 ),N (4,
),N (4,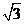 )且f(2)=2,
)且f(2)=2,
则f(6)= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com