
题型1:数量积的概念
例1.判断下列各命题正确与否:
(1)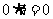 ;
;
(2)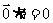 ;
;
(3)若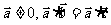 ,则
,则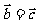 ;
;
(4)若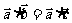 ,则
,则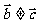 当且仅当
当且仅当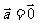 时成立;
时成立;
(5)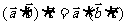 对任意
对任意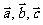 向量都成立;
向量都成立;
(6)对任意向量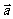 ,有
,有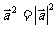 。
。
解析:(1)错;(2)对;(3)错;(4)错;(5)错;(6)对。
点评:通过该题我们清楚了向量的数乘与数量积之间的区别于联系,重点清楚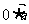 为零向量,而
为零向量,而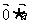 为零.
为零.
例2. 已知△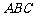 中,过重心
中,过重心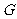 的直线交边
的直线交边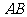 于
于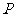 ,交边
,交边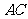 于
于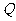 ,设△
,设△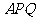 的面积为
的面积为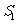 ,△
,△ 的面积为
的面积为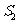 ,
, ,
,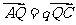 ,则(ⅰ)
,则(ⅰ)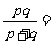 (ⅱ)
(ⅱ)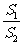 的取值范围是
.
的取值范围是
.
[解析]设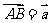 ,
,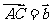 ,
,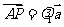 ,
,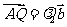 ,因为
,因为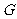 是△
是△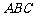 的重心,故
的重心,故
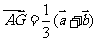 ,又
,又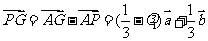 ,
, ,因为
,因为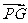 与
与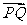 共线,所以
共线,所以 ,即
,即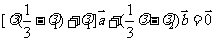 ,又
,又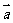 与
与 不共线,所以
不共线,所以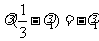 及
及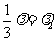 ,消去
,消去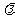 ,得
,得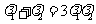 .
.
(ⅰ) ,故
,故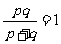 ;
;
(ⅱ)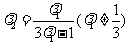 ,那么
,那么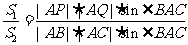

 ,当
,当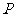 与
与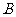 重合时,
重合时, ,当
,当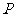 位于
位于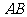 中点时,
中点时,
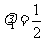 ,故
,故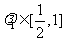 ,故
,故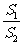
 但因为
但因为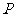 与
与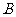 不能重合,故
不能重合,故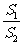
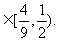

(2)设 、
、 、
、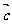 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①( ·
· )
)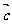 -(
-(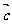 ·
· )
) =
= ②|
②| |-|
|-| |<|
|<| -
- | ③(
| ③( ·
·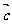 )
) -(
-(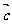 ·
· )
) 不与
不与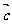 垂直
垂直
④(3 +2
+2 )(3
)(3 -2
-2 )=9|
)=9| |2-4|
|2-4| |2中,是真命题的有( )
|2中,是真命题的有( )
A.①②
B.②③ C.③④ D.②④
解析:(1)答案:D;因为 ,而
,而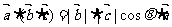 ;而
;而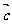 方向与
方向与 方向不一定同向.
方向不一定同向.
(2)答案:D①平面向量的数量积不满足结合律。故①假;②由向量的减法运算可知| |、|
|、| |、|
|、| -
- |恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因为[(
|恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因为[( ·
·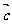 )
) -(
-(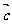 ·
· )
) ]·
]·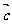 =(
=( ·
·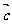 )
) ·
·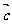 -(
-(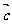 ·
· )
) ·
·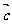 =0,所以垂直.故③假;④(3
=0,所以垂直.故③假;④(3 +2
+2 )(3
)(3 -2
-2 )=9·
)=9· ·
· -4
-4 ·
· =9|
=9| |2-4|
|2-4| |2成立。故④真。
|2成立。故④真。
点评:本题考查平面向量的数量积及运算律,向量的数量积运算不满足结合律。
题型2:向量的夹角
例3.(1)过△ABC的重心任作一直线分别交AB,AC于点D、E.若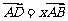 ,
, ,
,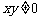 ,则
,则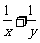 的值为( )
的值为( )
(A)4
(B)3 (C)2
(D)1
解析:取△ABC为正三角形易得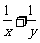 =3.选B.
=3.选B.
评析:本题考查向量的有关知识,如果按常规方法就比较难处理,但是用特殊值的思想就比较容易处理,考查学生灵活处理问题的能力.
(2)已知向量 =(cos
=(cos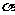 ,sin
,sin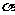 ),
), =(cos
=(cos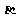 ,sin
,sin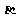 ),且
),且
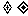
 ,那么
,那么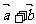 与
与 的夹角的大小是
。
的夹角的大小是
。
(3)已知两单位向量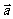 与
与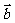 的夹角为
的夹角为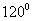 ,若
,若 ,试求
,试求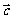 与
与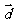 的夹角。
的夹角。
(4)|  |=1,|
|=1,|  |=2,
|=2,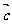 =
=  +
+  ,且
,且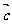 ⊥
⊥ ,则向量
,则向量 与
与 的夹角为 ( )
的夹角为 ( )
A.30° B.60° C.120° D.150°
解析:(2)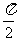 ;
;
(3)由题意,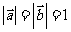 ,且
,且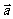 与
与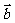 的夹角为
的夹角为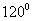 ,
,
所以,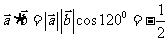 ,
,
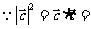
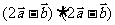
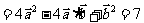 ,
,
 ,
,
同理可得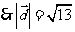 。
。
而
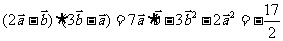 ,
,
设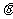 为
为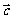 与
与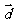 的夹角,
的夹角,
则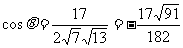 。
。
(4)C;设所求两向量的夹角为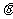


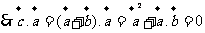

 即:
即: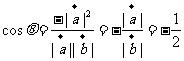

所以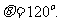

点评:解决向量的夹角问题时要借助于公式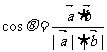 ,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于
,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于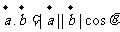 这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握.
这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握.
例4.(1)设平面向量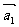 、
、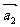 、
、 的和
的和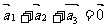 。如果向量
。如果向量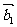 、
、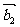 、
、 ,满足
,满足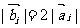 ,且
,且 顺时针旋转
顺时针旋转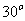 后与
后与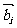 同向,其中
同向,其中 ,则( )
,则( )
A.-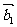 +
+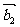 +
+ =
= B.
B.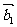 -
-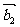 +
+ =
=

C.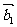 +
+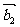 -
- =
= D.
D.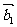 +
+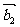 +
+ =
=
(2)(2009广东卷理)已知向量 与
与 互相垂直,其中
互相垂直,其中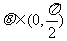 .
.
(1)求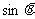 和
和 的值;
的值;
(2)若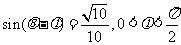 ,求
,求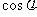 的值.
的值.
解 (1)∵ 与
与 互相垂直,则
互相垂直,则 ,即
,即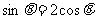 ,代入
,代入 得
得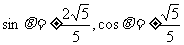 ,又
,又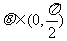 ,
,
∴ .
.
(2)∵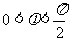 ,
,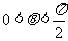 ,∴
,∴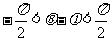 ,
,
则 ,
,
2、(山东临沂2009年模拟)如图,已知△ABC中,|AC|=1,∠ABC= ,∠BAC=θ,记
,∠BAC=θ,记 。
。
(1) 求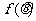 关于θ的表达式;
关于θ的表达式;
(2) 求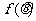 的值域。
的值域。
解:(1)由正弦定理,得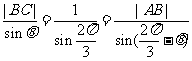
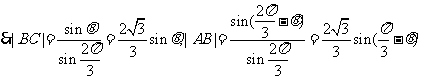

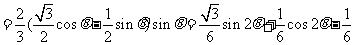
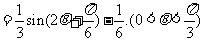
(2)由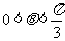 ,得
,得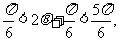
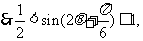
∴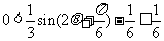 ,即
,即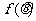 的值域为
的值域为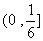 .
.
2.向量的应用
(1)向量在几何中的应用;
(2)向量在物理中的应用。
1.向量的数量积
(1)两个非零向量的夹角
已知非零向量a与a,作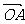 =
= ,
,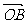 =
= ,则∠AOA=θ(0≤θ≤π)叫
,则∠AOA=θ(0≤θ≤π)叫 与
与 的夹角;
的夹角;
说明:(1)当θ=0时, 与
与 同向;
同向;
(2)当θ=π时, 与
与 反向;
反向;
(3)当θ=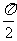 时,
时, 与
与 垂直,记
垂直,记 ⊥
⊥ ;
;
(4)注意在两向量的夹角定义,两向量必须是同起点的,范围0°≤q≤180°。
|


(2)数量积的概念
已知两个非零向量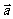 与
与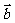 ,它们的夹角为
,它们的夹角为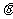 ,则
,则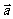 ·
·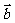 =︱
=︱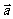 ︱·︱
︱·︱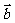 ︱cos
︱cos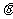 叫做
叫做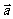 与
与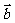 的数量积(或内积)。规定
的数量积(或内积)。规定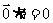 ;
;
向量的投影:︱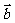 ︱cos
︱cos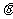 =
=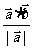 ∈R,称为向量
∈R,称为向量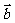 在
在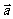 方向上的投影。投影的绝对值称为射影;
方向上的投影。投影的绝对值称为射影;
(3)数量积的几何意义: 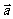 ·
·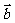 等于
等于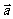 的长度与
的长度与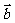 在
在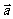 方向上的投影的乘积.
方向上的投影的乘积.
(4)向量数量积的性质
①向量的模与平方的关系: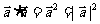 。
。
②乘法公式成立
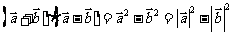 ;
;
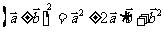
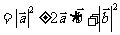 ;
;
③平面向量数量积的运算律
交换律成立: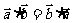 ;
;
对实数的结合律成立: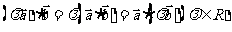 ;
;
分配律成立: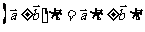
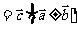 。
。
④向量的夹角:cos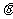 =
=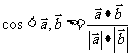 =
=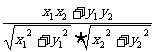 。
。
当且仅当两个非零向量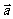 与
与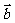 同方向时,θ=00,当且仅当
同方向时,θ=00,当且仅当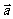 与
与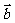 反方向时θ=1800,同时
反方向时θ=1800,同时 与其它任何非零向量之间不谈夹角这一问题.
与其它任何非零向量之间不谈夹角这一问题.
(5)两个向量的数量积的坐标运算
已知两个向量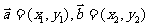 ,则
,则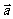 ·
·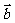 =
=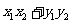 。
。
(6)垂直:如果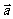 与
与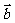 的夹角为900则称
的夹角为900则称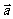 与
与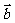 垂直,记作
垂直,记作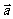 ⊥
⊥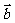 。
。
两个非零向量垂直的充要条件: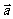 ⊥
⊥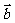
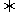
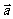 ·
·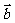 =O
=O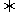
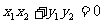 ,平面向量数量积的性质。
,平面向量数量积的性质。
(7)平面内两点间的距离公式
设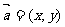 ,则
,则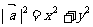 或
或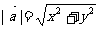 。
。
如果表示向量 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为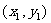 、
、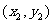 ,那么
,那么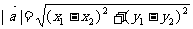 (平面内两点间的距离公式) .
(平面内两点间的距离公式) .
本讲以选择题、填空题考察本章的基本概念和性质,重点考察平面向量的数量积的概念及应用。重点体会向量为代数几何的结合体,此类题难度不大,分值5~9分。
平面向量的综合问题是“新热点”题型,其形式为与直线、圆锥曲线、三角函数等联系,解决角度、垂直、共线等问题,以解答题为主.
预测2010年高考:
(1)一道选择题和填空题,重点考察平行、垂直关系的判定或夹角、长度问题;属于中档题目.
(2)一道解答题,可能以三角、数列、解析几何为载体,考察向量的运算和性质;
2.向量的应用
经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程,体会向量是一种处理几何问题、物理问题等的工具,发展运算能力和解决实际问题的能力。
1.平面向量的数量积
①通过物理中"功"等实例,理解平面向量数量积的含义及其物理意义;
②体会平面向量的数量积与向量投影的关系;
③掌握数量积的坐标表达式,会进行平面向量数量积的运算;
④能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系。
32.(3分)世界卫生组织已把铝列为食品污染源之一,规定每人每天的摄入量控制在0.004g以下。若在1 kg的米面食品中加入2 g明矾(明矾的化学式:KAl(SO4)2·12H2O),那么某人一天如果吃了100 g上述米面食品,通过计算说明他摄入的铝的量是否在安全范围之内。
31.(3分)实验室用回收的60 g 10%的稀硫酸和98%的浓硫酸(密度:1.84g·cm-3)配制30%的硫酸溶液,需取浓硫酸多少毫升?可配得30%的硫酸多少克?
30.有一种不纯的一氧化碳气体,其中混有少量的水蒸气和二氧化碳。现提供下图所示的甲、乙、丙三种装置(每种都有若干个),若要达到以下两个目的:
(1)证明混有水蒸气和二氧化碳;
(2)除去水蒸气和二氧化碳。
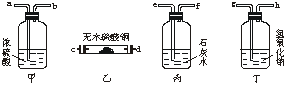
请回答:
(1)为了达到上述两个目的,请用各装置的代号表示出正确的连接顺序。
不纯的CO→________________________________→纯净的CO(3分)
(2)甲装置的作用是________________________________。
(3)乙装置的作用是________________________________。
(4)丙装置的作用是________________________________。
(5)丁装置的作用是________________________________。
29.有一种蓝色溶液具有下列性质:
(1)加入氢氧化钠溶液能生成蓝色沉淀;
(2)加入氯化钡溶液能生成白色沉淀,再加稀硝酸沉淀不溶解;
(3)放入一根铁钉,铁钉表面出现红色物质。
根据上述实验现象可知,这种蓝色溶液是__________(写化学式)溶液,写出上述变化的三个化学方程式:
(1)________________________________;
(2)________________________________;
(3)________________________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com