
28.(2009安徽卷理)给定两个长度为1的平面向量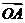 和
和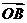 ,它们的夹角为
,它们的夹角为 .
.
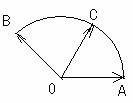 如图所示,点C在以O为圆心的圆弧
如图所示,点C在以O为圆心的圆弧 上变动.
上变动.
若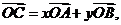 其中
其中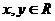 ,则
,则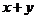
的最大值是________.
答案 2
解析
设
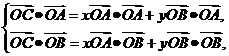 ,即
,即
∴
27.(2009江苏卷)已知向量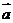 和向量
和向量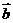 的夹角为
的夹角为 ,
, ,则向量
,则向量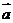 和向量
和向量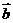 的数量积
的数量积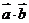 =
.
=
.
答案 3
解析 考查数量积的运算。 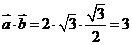
26. (2009广东卷理)若平面向量
(2009广东卷理)若平面向量 ,
, 满足
满足 ,
, 平行于
平行于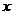 轴,
轴, ,则
,则 .
. 

TWT答案 (-1,0)-(-2,-1)=(-3,1)
解析
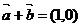 或
或 ,则
,则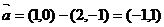
或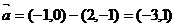 .
.
26.(2009湖北卷文)函数 的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于 ( )
的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于 ( )
A.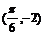 B.
B.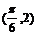 C.
C.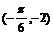 D.
D.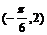
答案 D
解析
由平面向量平行规律可知,仅当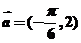 时,
时,
 :
: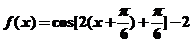 =
= 为奇函数,故选D.
为奇函数,故选D.
25.(2009湖北卷理)函数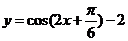 的图象
的图象 按向量
按向量 平移到
平移到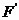 ,
,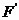 的函数解析式为
的函数解析式为 当
当 为奇函数时,向量
为奇函数时,向量 可以等于 ( )
可以等于 ( )
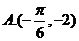
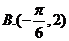
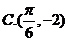
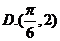
答案 B
解析
直接用代入法检验比较简单.或者设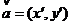 ,根据定义
,根据定义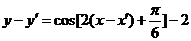 ,根据y是奇函数,对应求出
,根据y是奇函数,对应求出 ,
,
24.(2009重庆卷文)已知向量 若
若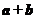 与
与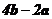 平行,则实数
平行,则实数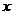 的值是 ( )
的值是 ( )
A.-2 B.0 C.1 D.2
答案 D
解法1
因为 ,所以
,所以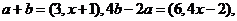
由于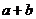 与
与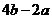 平行,得
平行,得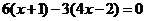 ,解得
,解得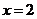 。
。
解法2 因为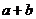 与
与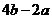 平行,则存在常数
平行,则存在常数 ,使
,使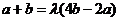 ,即
,即
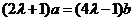 ,根据向量共线的条件知,向量
,根据向量共线的条件知,向量 与
与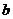 共线,故
共线,故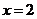
23.(2009重庆卷理)已知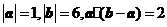 ,则向量
,则向量 与向量
与向量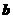 的夹角是( )
的夹角是( )
A.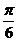 B.
B. C.
C.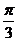 D.
D.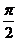


答案 C
解析
因为由条件得
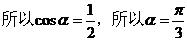
22.(2009福建卷文)设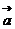 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足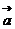 与
与 不共线,
不共线,
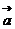

 ∣
∣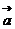 ∣=∣
∣=∣ ∣,则∣
∣,则∣ •
• ∣的值一定等于
∣的值一定等于
 ( )
( )
A.以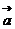 ,
, 为邻边的平行四边形的面积
为邻边的平行四边形的面积
B. 以 ,
, 为两边的三角形面积
为两边的三角形面积
C.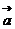 ,
, 为两边的三角形面积
为两边的三角形面积
D. 以 ,
, 为邻边的平行四边形的面积
为邻边的平行四边形的面积
答案 A
解析
假设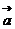 与
与 的夹角为
的夹角为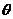 ,∣
,∣ •
• ∣=︱
∣=︱ ︱·︱
︱·︱ ︱·∣cos<
︱·∣cos< ,
, >∣
>∣
=︱ ︱·︱
︱·︱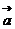 ︱•∣cos(90
︱•∣cos(90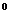
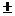
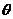 )∣=︱
)∣=︱ ︱·︱
︱·︱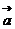 ︱•sin
︱•sin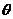 ,即为以
,即为以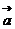 ,
, 为邻边的平
为邻边的平
行四边形的面积.
21.(2009湖南卷理)对于非0向时a,b,“a//b”的正确是 ( )
A.充分不必要条件 B. 必要不充分条件
C.充分必要条件 D. 既不充分也不必要条件
答案 A
解析
由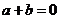 ,可得
,可得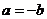 ,即得
,即得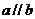 ,但
,但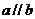 ,不一定有
,不一定有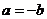 ,所以“
,所以“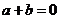 ”是“
”是“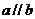 的充分不必要条件。
的充分不必要条件。
20.(2009宁夏海南卷文)已知 ,向量
,向量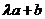 与
与 垂直,则实数
垂直,则实数 的值为 ( )
的值为 ( )
A.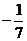 B.
B. C.
C.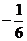 D.
D.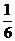
答案 A
解析
向量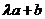 =(-3
=(-3 -1,2
-1,2 ),
), =(-1,2),因为两个向量垂直,故有(-3
=(-1,2),因为两个向量垂直,故有(-3 -1,2
-1,2 )×(-1,2)=0,即3
)×(-1,2)=0,即3 +1+4
+1+4 =0,解得:
=0,解得: =
=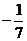 ,故选.A.
,故选.A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com