1、求三角函数最值的常用方法有：(1)配方法；(2)化为一个角的三角函数形式，如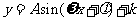等，利用三角函数的有界性求解；(3)数形结合法；(4)换元法；(5)基本不等式法等.

3.由学生小结，对教学效果作外显性评价。

2.对学生在学习过程中的表现，给予适度评价；

1.摆正教学过程中，师生的位置，把学习的权利真正交给学生，让学生成为学习的主人；

8.说明师生双边活动：教学过程的始终都在进行双边活动。

7.布置作业：书P68-理解与感受1、2、3

6.进入例习题的教学：(5-8分钟)

①例1(2)是个多答案的开放问题，其答案有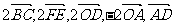：，在此为后继课的向量的数乘埋下伏笔；(3)强调是。

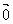②讲授例2。

③课堂练习：书P63(10分钟)

5.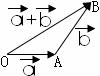进入向量加法的教学：(用时15分钟左右)(发放教具)

①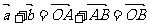此处让学生活动；在介绍完向量加法的三角形法则以后，我特别强调了其中反映出来的沙尔定理：

即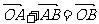，从左往右看，“合二为一”的功能，从右往左看，“一分为二”的功能；

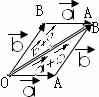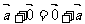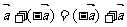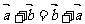②运用了由特殊到一般的认识、思维过程，由零向量、相反向量的满足的交换律，联想到非零向量是否满足交换律，并给予了几何证明。即由、，联想到，并给予如图几何证明

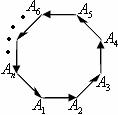③由非零向量的几何证明的构图，进行正迁移，得出平行四边形法则。此处让学生活动。

④沙尔定理为思考题埋下了伏笔，也用到了相反向量的和为零向量。

3.创设情境导入新课：

利用类比进行联想，激发学习欲望(用时0.5分钟)